Franz J. Vesely > MolSim Tutorial > NEMD I: Non-Hamiltonian Mthods 
 
 





 
< >
Vesely MolSim Tutorial




5 Molecular Dynamics far from Equilibrium

There are at least two good reasons to study non-equilibrium systems:
  • to determine by simulation transport coefficients $\eta, \lambda, D$ etc. and if possible their frequency dependence;
  • more generally, to understand the statistical mechanics of non-equilibrium; one attractive topic in this context is the emergence of irreversibility from reversible dynamics.

Subsections



5.1 Results of Linear Response Theory

We wish to develop relations between macroscopic transport coefficients and microscopic averages - which hopefully may be evaluated in simulation experiments.

Let $H_{0}$ be the Hamiltonian of the given system when it is isolated. If we apply a weak disturbing field $F(t)$ that couples to some property $A(\Gamma)$ (with $<A>=0$) the Hamiltonian of the perturbed system is given by

$ H=H_{0}-A \cdot F(t) $

Linear response theory then leads to the following first order expression for the mean temporal change of $A$:

$ <\dot{A}(t)> = \frac{\textstyle 1}{\textstyle kT} \int_{-\infty}^{t} dt' F(t')<\dot{A}(t)\dot{A}(t-t')>_{0} $

where the average $<>_{0}$ is to be taken over the unperturbed system. Assuming a constant field $F(t)=F$ switched on in the distant past we may write this as

$ <\dot{A}> = \frac{\textstyle F}{\textstyle kT} \int_{-\infty}^{0} dt' <\dot{A}(0)\dot{A}(-t')>_{0} $

Independently, the fundamental Green-Kubo relations tell us that for any conserved quantity $A$ the appropriate transport coefficient is given by the equilibrium average



$ \nu \equiv \int_{0}^{\infty}dt' <\dot{A}(0)\dot{A}(t')>_{0} $      (2)
Combining this with the above equation we find that $<\dot{A}> = \frac{\textstyle F}{\textstyle kT} \nu$, or

$ \nu = \frac{\textstyle kT}{\textstyle F} <\dot{A}> $

Thus we may determine the transport coefficient $\nu$ either from an equilibrium simulation using equ. 2, or from a non-equilibrium simulation with applied field using equ. 1 Generally the second method yields better statistics but is more prone to nonlinearity problems (large fields); also, systems responding to an external field must be thermostated.

Example: Consider a fluid sample of ions in an electric field $\vec{F}(t)\equiv \vec{E}(t)$. The charge distribution is described by the quantity $\vec{A}(t) \equiv \sum_{i}q_{i}\vec{r}_{i}(t)$ which couples to the field according to

$ \Delta H = - \vec{A} \cdot \vec{F} = -\left( \sum_{i}q_{i} \vec{r}_{i}\right) \cdot \vec{E}(t) $

The electrical current density $\vec{j}$ is defined by

$ \dot{\vec{A}} = \sum_{i}q_{i} \dot{\vec{r}}_{i}(t) \equiv V \vec{j}(t) $

($V$... volume).

Now consider the conductivity $\sigma$. It may be determined in two ways:
  • In an equilibrium simulation, using the Green-Kubo relation

    $ \sigma = \frac{\textstyle 1}{\textstyle kT} \int_{0}^{\infty} dt < j_{x}(0) j_{x}(t) >_{0} $

  • In a non-equilibrium simulation, using the measured response to an applied field $\vec{E}=\{E_{x},0,0\}$:

    $ \sigma = \frac{\textstyle < j_{x} > }{\textstyle E_{x}} $

Note: In the derivation of equ. 1 it is sufficient but not necessary that the external perturbation may be formulated as an additional term in the Hamiltonian. It is only necessary that the equations of motion contain perturbative terms which have to fulfill certain requirements. Specifically, the set

$ \begin{eqnarray} \dot{\vec{q}}_{i} &=& \vec{p}_{i} + A_{p} F(t) \\ \dot{\vec{p}}_{i} &=& \vec{K}_{i} + A_{q} F(t) \end{eqnarray} $


will be consistent with equ. 1 if only

$ \left( \vec{\nabla}_{q} \cdot A_{p}- \vec{\nabla}_{p} \cdot A_{q}\right) \cdot F(t)=0 $

(Note that we have switched to the Hamiltonian $q,p$ formalism.)

Example: In the Hamiltonian case $\Delta H = -A \cdot F$ the equations of motion are

$ \begin{eqnarray} \dot{\vec{q}} &=& \vec{\nabla}_{p} H = \vec{p}+\left( \vec{\nabla}_{p} A \right) \cdot F(t) \\ \dot{\vec{p}} &=& -\vec{\nabla}_{q} H = \vec{K} + \left( \vec{\nabla}_{q} A \right) \cdot F(t) \end{eqnarray} $


Therefore we have $A_{p}=\vec{\nabla}_{p}A$ and $A_{q}=\vec{\nabla}_{q}A$, and the requirement 3 is trivially fulfilled.



Viscosity: Non-Hamiltonian methods


Subsections

Gosling and Singer

[Mol.Phys.26(1973)1475]
An external force $\vec{F}=\{F_{x},0,0\}$ is introduced in the equations of motion according to

$ F_{i,x}=F_{0}\sin k z_{i} \;\;\;\;{\rm with}\;\;\;\; k\equiv 2 \pi \frac{\textstyle m}{\textstyle L}; \;\; m=1,2,\dots $

(Note: $\vec{A}_{q}=\{\sin kz, 0, 0 \}$ and $\vec{A}_{p}=0$ which fulfills 3.)

This will eventually lead to an average velocity profile which theoretically should look like

$ < v_{i,x} > =\frac{\textstyle n}{\textstyle k^{2}\eta} F_{0} \sin kz_{i}=v_{0} \sin kz_{i} $

where $n \equiv N/V$. Fitting the actual velocity profile to this expression we find $v_{0}$ and from that the $k$-dependent viscosity:

$ \eta(k)=\frac{\textstyle nF_{0}}{\textstyle v_{0}k^{2}} $

Repeating the calculation for several values of $k$ and extrapolating to $k \rightarrow 0$ we find an estimate for $\eta \equiv \eta(k=0)$

Note: The applied force does work against the viscous forces, thus inducing an undesirable temperature rise.

Ashurst and Hoover

[Phys.Rev.Lett 31(1973)206]

These authors use periodic boundary conditions in the $x,y$ directions; the upper and lower boundaries are replaced by layers containing trapped particles. The upper layer has a mean velocity $u_{x}$ while the bottom layer is at rest.
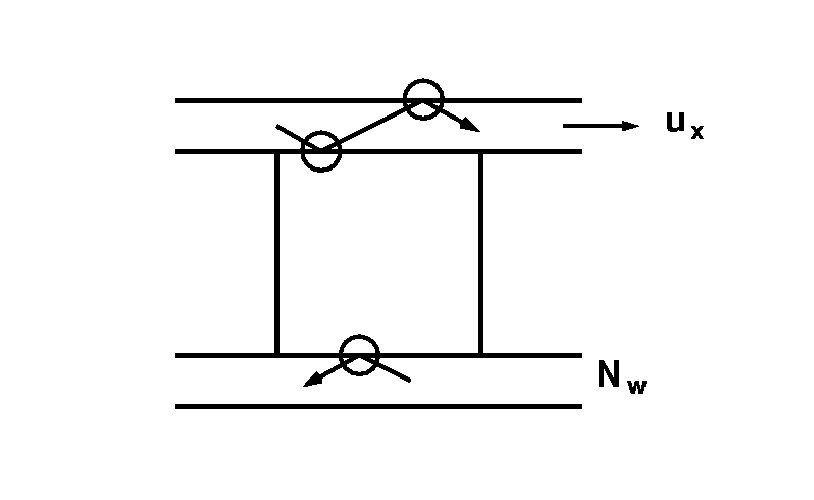
Figure 8.1: Moving boundary region: the $N_{w}$ wall particles remain trapped in the layer. An external force keeps up the relative velocity of the upper and lower boundary layers.


The desired shear rate is $\gamma = u_{x}/L$. We need an external force

$ \vec{F}(t)=-\sum_{i}^{N_{w}}\sum_{j}^{N} \vec{K}_{ij}(t)/N_{w} $

to achieve this. This force is proportional to the viscosity.

Again, the temperature will slowly increase due to the work done by the external force.

Lees and Edwards

[Lees+Edwards, J.Phys.C 5(1972)1921; Evans-Morriss Mol.Phys. 37(1979)1745; Comp.Phys.Rep. 1(1984)297]

Lees and Edwards suggested a method to combine laminary flow with periodic boundaries in the $z$ direction:

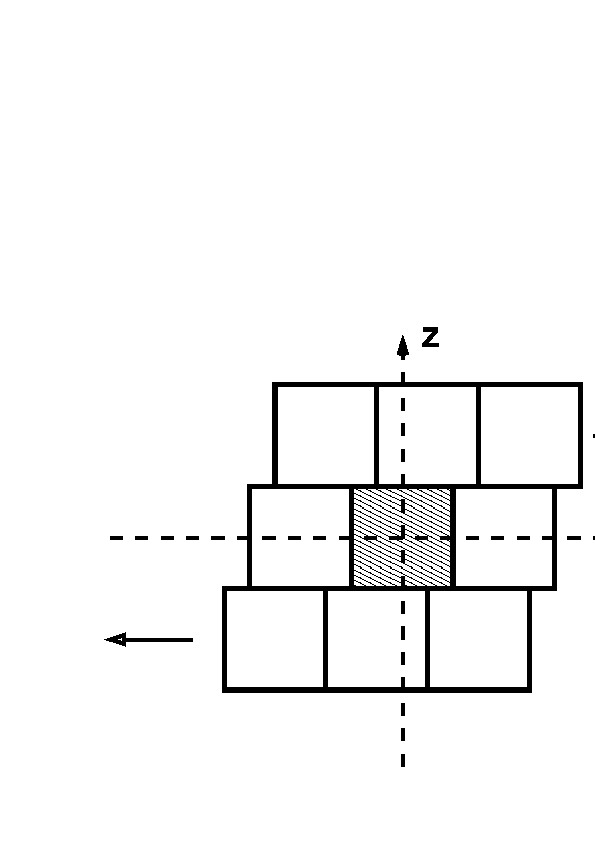
Figure 8.2: Lees-Edwards boundary conditions. The coordinate origin is in the center of the middle cell. Upper and lower replicas are counter-moving at constant speeds $u_{x}=\pm \gamma L$.


Here are in language-independent form, the appropriate code parts for PBC and NIC: 

// Periodic boundary conditions:
// round(float) is the integer next to float
// L is the cell side length; note that x,y,z vary between -L/2 and L/2
// t is the elapsed time
// gamma is the shear rate
       cz=round(z/L)
       cx=x-cz*gamma*L*t
       x=cx-round(x/L)*L
       y=y-round(y/L)*L
       z=z-cz*L
       .....


// Nearest image convention:
       delx=x(j)-x(i)
       ...
       cz=round(dz/L)
       cdelx=delx-cz*gamma*L*t
       delx=cdelx-round(cdelx/L)*L
       dely=dely-round(dely/L)*L
       delz=delz-cz*L
       ...


This is the procedure for a single time step:
  • Compute all forces, applying the nearest image convention
  • Integrate the equs. of motion for $t_{n} \rightarrow t_{n+1}$
  • Perform a least squares fit to a linear velocity profile, determining $u_{0}$ and $\gamma'$ such that

    $ v_{i,x}=u_{0}+\gamma' \left( z_{i}\right) + c_{i,x} $

    where $c_{i,x}$ is the thermal velocity of the particle.
  • Apply a simple thermostat by adjusting all $v_{i,x},v_{i,y}$ such that

    $ \sum_{i} \frac{\textstyle m}{\textstyle 2}\left( v_{i,x}^{2}+v_{i,y}^{2}\right)=NkT $

  • Compute the stress tensor element

    $ \sigma_{xz} \equiv \sum_{i} \left[ m v_{i,x} v_{i,z}+K_{i,x} z_{i} \right] $

From the average stress we find $\eta$:

$ <\sigma_{xz}>=-\eta \gamma $


vesely may-06

< >