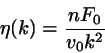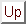

[Mol.Phys.26(1973)1475]
An external force
 is introduced in the
equations of motion according to
is introduced in the
equations of motion according to
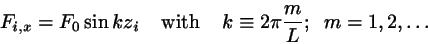 |
(8.15) |
(Note:
 and
and 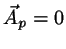 which fulfills 8.12.)
which fulfills 8.12.)
This will eventually lead to an average velocity profile which
theoretically should look like
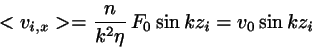 |
(8.16) |
where 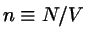 .
Fitting the actual velocity profile to this expression we find
.
Fitting the actual velocity profile to this expression we find  and from that the
and from that the 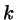 -dependent viscosity:
-dependent viscosity:
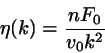 |
(8.17) |
Repeating the calculation for several values of 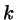 and extrapolating
to
and extrapolating
to
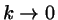 we find an estimate for
we find an estimate for
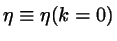
Note:
The applied force does work against the viscous forces, thus inducing
an undesirable temperature rise.

 F. J. Vesely / University of Vienna
F. J. Vesely / University of Vienna