|
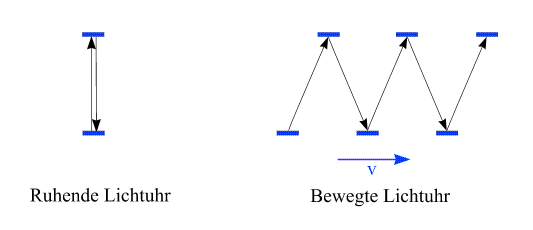
Ein leicht nachvollziehbarer Einstieg in die Herleitung der Effekte der Speziellen Relativitätstheorie aus den grundlegenden Postulaten bildet das Gedankenexperiment der Lichtuhr. Unter einer Lichtuhr wird eine Vorrichtung gegebener Länge verstanden, entlang der ein Photon hin- und herpendelt:
In dieser Abbildung sind die Begrenzungen der Lichtuhr in blau dargestellt. Wir können uns darunter zwei Spiegel vorstellen, die in einem gegebenen Abstand zueinander fixiert sind. Die linke Grafik zeigt die Lichtuhr vom Standpunkt eines Beobachters, der sich ihr gegenüber in Ruhe befindet, d.h. vom Standpunkt ihres Ruhsystems. Wir fragen nun, wie derselbe Prozess in einem dagegen bewegten Inertialsystem aussieht, wobei die Bewegungsrichtung quer zur Laufrichtung der Photonen stattfinden soll. Für einen Beobachter in diesem neuen System bewegt sich die Lichtuhr, und wir bezeichnen den Wert ihrer Geschwindigkeit mit v. Die Photonen werden im bewegten System entlang schräger Bahnen laufen - das ist im rechten Teil der obigen Abbildung dargestellt. Wir können uns auch genausogut vorstellen, dass zwei Lichtuhren identischer Bauart zur Verfügung stehen und wir eine ruhende (links) und eine mit Geschwindigkeit v bewegte (rechts) betrachten. Nach der galileischen
Physik wäre zu erwarten, dass sich das von einem (quer zur Laufrichtung)
bewegten Inertialsystem aus beobachtete Photon schneller als
im Ruhsystem der Lichtuhr bewegt. So könnte man etwa argumentieren,
dass die Geschwindigkeitskomponente in senkrechter Richtung c
und in horizontaler Richtung v
ist, der Betrag der Geschwindigkeit also insgesamt den Wert
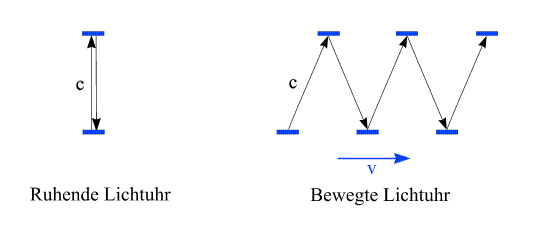
Nun kommt das Postulat von der Konstanz der Lichtgeschwindigkeit ins Spiel. Die Photonen haben in jedem Inertialsystem die Geschwindigkeit c. Das führt zu einer für die galileische Physik unangenehmen Konsequenz:
Alle hier dargestellten Photonen haben dieselbe Geschwindigkeit. Die Wegstrecke vom unteren bis zum oberen Spiegel ist jedoch für das Photon der bewegten Lichtuhr länger als für das der ruhenden Lichtuhr, und daher vergeht eine größere Zeitspanne, bis es vom einen zum anderen Spiegel gelangt! Für die Konstanz der Lichtgeschwindigkeit muss also ein Preis gezahlt werden: Die Zeitdauer, die ein Prozess in einem Inertialsystem dauert, ist nicht unbedingt gleich der Zeitdauer, die während desselben Prozesses in einem anderen Inertialsystem vergeht. Die bewegte Lichtuhr hat eine längere Periodendauer als die ruhende. Das bedeutet, dass der Vorgang des Photonenpendelns, wenn er von einem bewegten System aus beobachtet wird, langsamer ist als im Ruhsystem der Lichtuhr. Da nun eine solche Lichtuhr dazu benutzt werden kann, die Zeitdauer beliebiger anderer Prozesse zu messen (sie ist ja letztlich tatsächlich nur eine besondere Art von "Uhr"), ist dieser Effekt nicht auf Lichtuhren beschränkt, sondern betrifft den Zeitfluss in beiden Systemen ganz generell. Er wird oft in knapper Weise mit den Worten "Bewegte Uhren gehen langsamer" zusammengefasst
und heißt Zeitdilatation ("Zeitdehnung").
Die Zeit, die für eine Uhr in ihrem Ruhsystem vergeht, heißt
Eigenzeit.
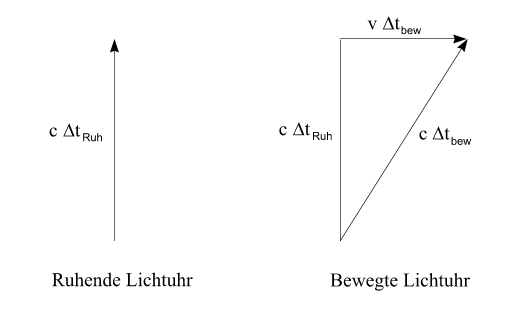
Die soeben gemachte Aussage, dass eine Uhr in einem relativ zu ihr bewegten Inertialsystem langsamer geht als in ihrem Ruhsystem, lässt sich quantitativ präzisieren. Betrachten wir die Bewegung des Photons vom unteren bis zum oberen Spiegel. Alle Längen, die in dieser Situation auftreten, sind in der folgenden Abbildung angegeben:
Analysieren wir die Eintragungen in dieser Skizze:
Unsere bisher nur qualitative Argumentation können wir nun in einer Formel ausdrücken: Dtbew > DtRuh. Um die Größe des Effekts quantitativ zu bestimmen, wenden wir den Satz von Pythagoras auf das rechtwinkelige Dreieck im rechten Teil der obigen Abbildung an:
und lösen nach Dtbew auf. Wir erhalten
Das
ist die Formel für die
Zeitdilatation,
die wir kompakter auch als
Dabei handelt es sich nicht um eine Art "scheinbaren Effekt" oder eine "Täuschung" - es sind hier die tatsächlichen Zeiten betroffen, wie sie mit (hinreichend genauen) Uhren beliebiger Bauart gemessen werden können. Die Zeitdauer, die ein Prozess in Anspruch nimmt, ist keine universelle Größe, sondern hängt vom Bewegungszustand des Beobachters ab. Die "Zeit" hat ihren absoluten Charakter - den sie in der galileischen Physik hatte - verloren. Im
Zuge unserer Argumentation haben wir stillschweigend vorausgesetzt,
dass der Abstand zwischen den Spiegeln in beiden Systemen gleich groß
ist. Wir werden im nächsten Abschnitt, der von der Lorentzkontraktion handelt, feststellen, dass nicht nur Zeitintervalle, sondern
auch räumliche Abstände vom Bewegungszustand des Beobachters
abhängen. Allerdings betrifft dieser Effekt nur Längen in
die relative Bewegungsrichtung der beiden Systeme. Wir haben, mit anderen
Worten, stillschweigend vorausgesetzt, dass Längen quer
zur Bewegungsrichtung in beiden Systemen gleich gross sind. Das lässt
sich mit ein bisschen mehr Aufwand aus den Postulaten
ableiten - wir wollen es aber bei der hier
vorgeführten vereinfachten Argumentation belassen.
Wir erhalten als Nebenprodukt unmittelbar ein weiteres physikalisches Resultat: Die Formel (2) macht keinen Sinn, wenn eine Geschwindigkeit v eingesetzt wird, deren Betrag größer oder gleich c ist. Offensichtlich müssen wir schließen, dass sich ein Inertialsystem relativ zu einem anderen nur mit Unterlichtgeschwindigkeit bewegen kann. Daher kann sich kein materielles Objekt, das in Bezug auf ein Inertialsystem in Ruhe sein kann, mit einer Geschwindigkeit, deren Betrag ³ c ist, bewegen. Das trifft auf alle Teilchen und Körper zu, die eine nichtverschwindende Masse haben. (Lediglich "masselose Teilchen" wie Photonen bilden hier eine Ausnahme: sie bewegen sich immer genau mit Lichtgeschwindigkeit - wir werden im Abschnitt über die Energie ein paar Worte über diese Teilchen sagen). Geschwindigkeiten, die größer sind als c, können für all diese Objekte nicht auftreten. Daraus folgt auch, dass es kein Signal gibt, das Informationen schneller als das Licht übertragen kann. Fassen wir zusammen (wobei v den Betrag der Geschwindigkeit bezeichnet):
Damit
haben wir eine der berühmtesten Aussagen der Speziellen Relativitätstheorie
(das "Verbot der Überlichtgeschwindigkeit") begründet.
Es folgt unmittelbar aus den Ausgangspostulaten. Der Faktor Eine dynamische Begründung der Aussage v < c für Körper mit nichtverschwindender Masse ergibt sich, wenn relativistische Versionen der Begriffe Masse und Energie entwickelt werden (siehe den Abschnitt über die Energie). Wir wollen hier nur erwähnen, dass der Ausdruck "Masse" genau genommen "Ruhemasse" heißen muss (wohingegen Photonen keine nichtverschwindende Ruhemasse zugeordnet werden kann), und dass die Beschleunigung eines Körpers, dessen Ruhemasse ¹ 0 ist, mehr Energie benötigt als zunächst vermutet. Die Beschleunigung eines solchen Körpers auf Lichtgeschwindigkeit würde unendlich viel Energie erfordern, ist also dynamisch unmöglich. Das alles mag zunächst ein bisschen eigenartig klingen, weil es unseren Alltagsvorstellungen von Geschwindigkeiten widerspricht. Was geschieht etwa, wenn sich ein Teilchen mit 3/4 der Lichtgeschwindigkeit in einem Zug, der selbst mit 3/4 der Lichtgeschwindigkeit fährt, nach vorne bewegt - müsste es sich im System der Schienen dann nicht mit eineinhalbfacher Lichtgeschwindigkeit bewegen? Die Antwort ist nein, und wie groß seine tatsächliche Geschwindigkeit ist, erfahren Sie im Abschnitt über die relativistische Geschwindigkeitsaddition. Es gibt ein häufig gehörtes Argument, das gegen die Überlichtgeschwindigkeit ins Treffen geführt werden kann: Sie führt zur Möglichkeit von Zeitreisen, also Reisen in die eigene Vergangenheit. Die Ausarbeitung einer genaueren Argumentation ist als Aufgabe im Abschnitt Kniffliges vorgesehen. (Um sie lösen zu können, sollte bereits in Grundzügen bekannt sein, was die Lorentztransformation ist). Wir wollen noch eine Warnung aussprechen: Das Verbot der "Überlichtgeschwindigkeit" bezieht sich nur auf die Bewegung physikalischer Objekte wie Körper, Teilchen, Photonen usw., also Bewegungen, mit deren Hilfe Information ("von einem Punkt zum nächsten") übertragen werden kann. Es können aber durchaus auch andere Formen von "Geschwindigkeiten" auftreten, die keinerlei Begrenzung unterworfen sind: In Vorträgen wird manchmal mit Hilfe eines Laserpointers ein Lichtpunkt auf einen Bildschirm projiziert. Wird der Laserpointer schnell gedreht, so flitzt der Lichtpunkt über den Bildschirm - die Geschwindigkeit, mit der er dies tut, kann im Prinzip durchaus größer als c sein (wenn der Bildschirm genügend weit entfernt ist), denn mit ihm ist nicht die Bewegung eines Objekts (oder die Übertragung von Information) "von einem Punkt zum nächsten" verbunden! In
der Teilchenphysik wird manchmal von "Tachyonen" gesprochen,
die sich mit Überlichtgeschwindigkeit bewegen. Dabei handelt es
sich tatsächlich um hypothetische überlichtschnelle Teilchen,
die in gewissen Theorien auftreten und dort Probleme machen. Es gibt
zwei Methoden, diese Probleme loszuwerden: (i) Eine Theorie,
in der Tachyonen auftreten, wird verworfen. (ii) Die Theorie
wird so geändert, dass die in ihr enthaltenen Tachyonen nicht mit
dem Rest der Welt wechselwirken und daher als rein mathematische Struktur
angesehen werden können, die in der physikalischen Realität
keine Entsprechung besitzt.
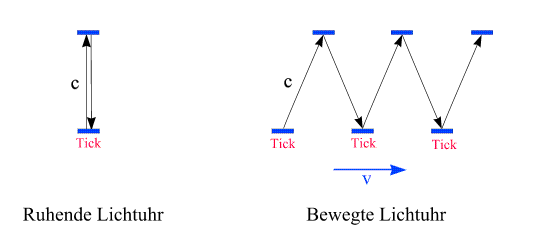
In der oben vorgeführten Argumentation wird eine räumlich ausgedehnte Konstruktion (bestehend aus zwei Spiegeln und einem zwischen ihnen pendelnden Photon) als "Uhr" verwendet. Wie jede Uhr kann sie dazu benutzt werden, Zeitintervalle zwischen Ereignissen zu messen - sie misst dabei direkt die Zeit, die "in ihrem Ruhsystem vergeht". Das ist nun allerdings ein schwieriger Begriff - zumal ja der universelle Zeitfluss (das synchrone Schlagen aller Uhren, unabhängig von ihrem Bewegungszustand, wie es in der galileischen Physik angenommen wird) aufgrund des Effekts der Zeitdilatation verloren gegangen ist. Einfacher ist die Vorstellung, eine Uhr sei sehr klein (im Grenzfall punktförmig) - also gewissermaßen ein "Teilchen", das in regelmäßigen Zeitabständen "tickt". Eine als punktförmig angenommene Uhr hat stets einen wohldefinierten Ort, und nur dort kann sie Zeitintervalle zwischen Ereignissen messen. Sie stellt das Konzept eines von einem Beobachter auf seinem Weg mitgenommenen Zeitmessers dar. Eine Zeitmessung ist dann - wie es auch in der physikalischen Praxis der Fall ist - zunächst eine Ablesung an einer solchen - hinreichend kleinen, lokalisierten - Uhr. (Die "globale" Zeit, die innerhalb eines Inertialsystems gilt, kommt erst durch die Synchronisation lokalisierter Uhren, die sich an verschiedenen Orten befinden und relativ zueinander ruhen, zustande. In der Einleitung haben wir kurz über die Synchronisation von Uhren gesprochen, und im Abschnitt Gleichzeitigkeit werden wir das Thema wieder aufnehmen). Es ist aber nicht schwierig, aus dem Konzept der Lichtuhr eine lokalisierte Uhr herauszufiltern: Wir können sie als jenen Punkt an einem der beiden Spiegel definieren, auf den das Photon in regelmäßigen Zeitabständen immer wieder auftrifft. Dies veranschaulicht die folgende Abbildung:
Das "Ticken" wird durch das wiederholte Auftreffen des Photons am unteren Spiegel repräsentiert, und es ist klar, dass sich eine derart konstruierte "Uhr" mit Geschwindigkeit v nach rechts bewegt. Zudem kann der Abstand zwischen den Spiegeln (und damit die Periodendauer) beliebig klein gemacht werden. Lokalisierte
Uhren können als Weltlinien in Raumzeit-Diagrammen dargestellt
werden. Weiters können sie nicht nur geradlinig gleichförmige,
sondern auch beschleunigte Bewegungen ausführen. Diesen beiden
Themen wenden wir uns nun noch kurz zu.
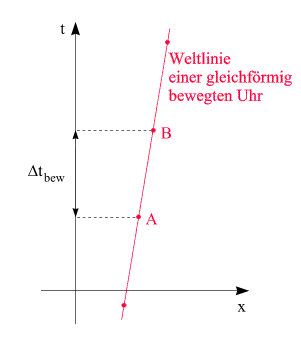
Die Weltlinie einer lokalisierten, in einem gegebenen Inertialsystem geradlinig gleichförmig bewegten Uhr kann in einem Raumzeit-Diagramm als Gerade dargestellt werden:
Auf
der Weltlinie sind Ereignisse als rote Punkte eingezeichnet, die das
"Ticken" repräsentieren, wovon zwei die Namen A
und B tragen.
Die Zeit Dtbew,
die zwischen ihnen im gegebenen Inertialsystem vergeht, kann direkt
abgelesen werden. (Man spricht daher auch von der Koordinatenzeit
in Bezug auf das gegebene System). Die Zeit DtRuh,
die zwischen A
und B im
Ruhsystem der Uhr - d.h. für die
Uhr selbst, man kann auch sagen: entlang ihrer Weltlinie -
vergeht, ist kürzer (obwohl die Verbindungsstrecke zwischen
A
und B im
Diagramm länger ist als ihr vertikaler Abstand
Dtbew ):
das ist der Effekt der Zeitdilatation. Allerdings kann die Zeit, die
für eine bewegte Uhr vergeht, in einem solchen Diagramm nicht
einfach als "Länge entlang ihrer Weltlinie" abgelesen
werden. Falls sie benötigt wird, kann sie mit Hilfe der Formel
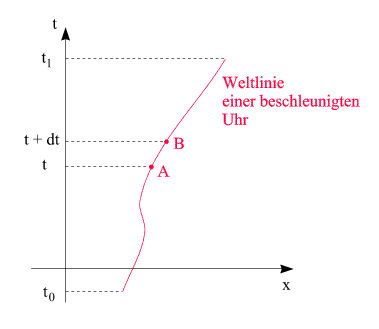
Obwohl der Effekt der Zeitdilatation - Formel (2) - nur für Uhren, die sich relativ zueinander mit konstanter Geschwindigkeit bewegen, hergeleitet worden ist, gilt er auch für beschleunigte Uhren. Um ihn korrekt zu formulieren, müssen wir
Nun sei dt
ein kleines (genauer: ein "infinitesimal kleines") Zeitintervall.
Zwischen den Zeiten t
und
Das Ereignis A
findet im System I
zur Zeit t statt,
das Ereignis B
zur Zeit
vergangen. (Unter
Durch eine Integration
lassen sich die in Formel (3) vorkommenden Zeiten aufsummieren: Führt
die Uhr zwischen den - im System I
gemessenen - Zeiten t0
und t1
eine beliebige beschleunigte Bewegung aus (siehe die obige Abbildung),
so vergeht für sie nicht das Zeitintervall
Experimentell ließe sich dieser Effekt einfach durch eine Ablesung an der beschleunigten Uhr bestätigen! In dieser Aussage steckt bereits der Effekt des Zwillingsparadoxons. Für den Spezialfall einer gleichförmig bewegten Uhr ( v(t) = const ) reduziert sie sich auf Formel (2). Die Aussagen (3) und (4) gelten auch für Bewegungen, die nicht geradlinig verlaufen: v(t)2 bedeutet dann das Quadrat des Geschwindigkeitsvektors (d.h. das Quadrat des Betrages des Geschwindigkeitsvektors). Aufgaben hierzu:
|