


Next: 4.1.4 Implicit Methods
Up: 4.1 Initial Value Problems
Previous: 4.1.2 Stability and Accuracy
4.1.3 Explicit Methods
- Euler-Cauchy (from DNGF; see above)
- Leapfrog algorithm (from DST):
This is an example of a multistep technique, as timesteps
 and
and  contribute
contribute  .
Stability analysis for such algorithms is as follows:
.
Stability analysis for such algorithms is as follows:
Let the explicit multistep scheme be written as
Inserting a slightly deviating solution
 and computing the difference, we have
and computing the difference, we have
We combine the errors at subsequent time steps to a vector
and define the quadratic matrix
Then
Stability is guaranteed if
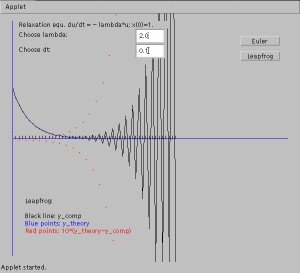
EXAMPLE 1:
Leapfrog / Relaxation equation:
Therefore
which means that
 , and
, and  , and
the matrix
, and
the matrix
 is
is
with eigenvalues
For real
 we find that
we find that  always, meaning
that the leapfrog scheme is unstable for the relaxation (or growth)
equation.
always, meaning
that the leapfrog scheme is unstable for the relaxation (or growth)
equation.
EXAMPLE 2:
Leapfrog / Harmonic oscillator:
and
For the amplification matrix we find
(with
 )
)
with eigenvalues
But the modulus of this is always  .
.
 The leapfrog
algorithm is marginally stable for the harmonic oscillator.
The leapfrog
algorithm is marginally stable for the harmonic oscillator.



Next: 4.1.4 Implicit Methods
Up: 4.1 Initial Value Problems
Previous: 4.1.2 Stability and Accuracy
Franz J. Vesely Oct 2005
See also: "Computational Physics - An Introduction," Kluwer-Plenum 2001
![]() and
and ![]() contribute
contribute ![]() .
Stability analysis for such algorithms is as follows:
.
Stability analysis for such algorithms is as follows:
![\begin{displaymath}
\mbox{$\bf y$}_{n+1}=\sum_{j=0}^{k}
\left[ a_{j}\mbox{$\bf y$}_{n-j}+b_{j}\Delta t \,\mbox{$\bf f$}_{n-j} \right]
\end{displaymath}](img805.png)





![\begin{displaymath}
g= \pm \left[ (1-\frac{\alpha^{2} \omega_{0}^{2}}{2})
\pm i ...
...\sqrt{1-\frac{\alpha^{2}
\omega_{0}^{2}}{4}} \; \right]^{1/2}
\end{displaymath}](img824.png)