Mit Hilfe dieser Diagramme lassen sich zahlreiche Eigenschaften des Wassers und seiner Aggregatzustände
– sowie auch anderer Stoffe – und damit grundlegende Tatsachen der Wärmelehre und des
Aufbaus der Materie diskutieren. Der dargestellte Prozess besteht darin, dass einem Kilogramm Eis bei
einer Temperatur von –40 °C
nach und nach Energie zugeführt wird, bis es sich schließlich in
150 °C
heißen Wasserdampf verwandelt hat. Während dieses Prozesses wird der Druck bei
1.01325 bar
(dem "Normaldruck", der dem mittleren Luftdruck auf Meereshöhe entspricht) konstant gehalten.
- Benötigte Energien:

- Wir beginnen mit 1 kg Eis
bei
einer Temperatur von –40 °C.
Auf der horizontalen Achse des Diagramms ist die Temperatur T
in °C aufgetragen,
auf der vertikalen Achse die Energie E,
die wir dem System ab nun in kleinen Portionen zuführen werden.
Der Nullpunkt der E-Achse hat keine absolute
Bedeutung, sondern entspricht lediglich dem Beginn des von uns betrachteten Prozesses.
- Zu Beginn befindet sich unser Kilogramm Eis also in jenem Zustand, der durch den Schnittpunkt der Achsen
dargestellt wird: T = –40 °C
und (da noch keine Energie zugeführt wurde)
E = 0.
- Führen wir dem System nun Energie zu, so erwärmt es sich. Das wird durch die leicht ansteigende rote Linie dargestellt.
Der Anstieg (die Steigung) dieser Linie entspricht der so genannten spezifischen Wärmekapazität.
Sie gibt ganz allgemein die Energie an, die einem Kilogramm
eines Stoffes zugeführt werden muss, um ihn um
1 °C
(was dasselbe ist wie 1 K)
zu erwärmen.
Die spezifische Wärmekapazität von Eis
hängt ein bisschen von der Temperatur ab.
Im dargestellten Temperaturbereich liegt sie um
2000 J/(kg·K)
oder
2 kJ/(kg·K).
Um unser Kilogramm Eis von der Anfangstemperatur
–40 °C auf
0 °C
zu erwärmen, ist daher eine Energie von etwa
40·2 kJ = 80 kJ
nötig.
- Wieviel Energie ist 1 kJ?
Welche Größenordnungen von Energien kommen im Diagramm vor?
- Um einen Vergleich mit mechanischen Energien zu haben, erinnern wir uns:
1 J
ist ungefähr die Energie, die nötig ist, um eine Tafel Schokolade
(0.1 kg) einen Meter
hoch zu heben.
- Mit einer Energie von 1 kJ
können wir also tausend Tafeln Schokolade
(etwa 100 kg)
einen Meter hoch heben.
- Mit einer Energie von 80 kJ
können wir eine Masse von einer Tonne (1000 kg,
was etwa einem Kubikmeter voll Wasser entspricht) ungefähr 8 Meter hoch heben.
Gerade eine solche Energiemenge ist nötig, um Eis von
–40 °C auf
0 °C
zu erwärmen. Sie ist etwas kleiner als die Abstände der Teilstriche auf der
E-Achse.
- Insgesamt reicht der dargestellte Teil der E-Achse bis
zu Energien um die 3000 kJ.
Das entspricht dem Hochheben von 10 Tonnen (also etwa 7 durchschnittlichen PKWs)
in eine Höhe von 30 m.
Steigt ein
70 kg schwerer Mensch
auf einen 4400 m hohen Berg, so
muss er seine potentielle Energie um diesen Betrag erhöhen.
Die Energiemengen, um die es hier geht, sind also beträchtlich, obwohl sie nur ein Kilogramm Wasser
betreffen.
- Was geschieht bei der Erwärmung von Eis?
Im festen Aggregatzustand sind die Moleküle durch elektromagnetische Kräfte
starr aneinander gebunden. Sie liegen ziemlich dicht gepackt nebeneinander und können sich weder frei bewegen
noch relativ zueinander drehen. Sie können aber gegeneinander schwingen.
Die Temperatur ist ein Maß für die Schwingungsenergie, die im Mittel auf ein einziges Molekül kommt.
Die einem Festkörper zugeführte Energie führt hauptsächlich dazu, dass diese Schwingungen
stärker werden – er erwärmt sich.
(Mehr über dieses "Stärker werden" weiter unten, beim Diagramm über die Volumina).
- Hat das Eis eine Temperatur von 0 °C
erreicht, so schmilzt es, d.h. es geht in den flüssigen Aggregatzustand über.
Die Temperatur, bei der dies passiert, ist für jeden Stoff charakteristisch (und hängt vom Druck ab). Sie wird Schmelztemperatur genannt.
Dem Diagramm entnehmen wir zwei wichtigen Eigenschaften des Schmelzprozesses:
- Das Schmelzen vollzieht sich (bei Normaldruck) bei einer gleichbleibenden Temperatur von
0 °C. Das bedeutet, dass
eine weitere Energiezufuhr zunächst nicht zu einer weiteren Erwärmung führt!
- Um unser Kilogramm Eis vollständig zu schmelzen, ist eine erhebliche Energiezufuhr nötig, die
so genannte Schmelzwärme von
333 kJ,
also etwa vier mal so viel wie zur Erwärmung des Eises von
–40 °C auf
0 °C
nötig war.
Schmelzen ist ein allmählicher Vorgang, bei dem festes Eis und flüssiges Wasser gleichzeitig existieren.
Je mehr Energie zugeführt wird, umso größer ist der Anteil des flüssigen Wassers,
bis schließlich kein Eis mehr vorhanden ist. Mit dem Ende dieses Prozesses ist der Beginn
(d.h. das linke Ende) der blauen Linie erreicht.
- Die während des Schmelzens zugeführte Energie löst die starren Bindungen zwischen den Molekülen.
Nach wie vor üben die Moleküle Kräfte aufeinander aus, können sich aber nun gegeneinander bewegen.
Daher passt sich eine Flüssigkeit – im Gegensatz zu einem Festkörper – der Form eines
Gefäßes an, in dem sie sich befindet.
- Das Schmelzen besitzt eine Umkehrung: das Gefrieren. Es tritt auf, wenn einer Flüssigkeit Energie entzogen wird,
wenn in unserem Diagramm also von oben nach unten gegangen wird. Dabei bilden sich die starren Verbindungen, die für
Festkörper charakteristisch sind, zuerst von kleinen "Kristallisationskernen" ausgehend, die dann "wachsen".
Dabei kann es zu dem Phänomen kommen, dass sich die ersten dieser Kristallisationskerne verzögert bilden, d.h. dass
die Gefriertemperatur unterhalb der Schmelztemperatur liegt. Kleinste Verunreinigungen führen aber in der Praxis dazu,
dass dies beim Gefrieren von Stoffen im Alltag nicht auftritt, d.h. dass die Gefriertemperatur
gleich der Schmelztemperatur (bei Wasser 0 °C)
ist. Die Energie, die dann dem Wasser entzogen werden muss, um es vollständig zu gefrieren, ist
gleich der Schmelzwärme.
- Führen wir nun unserem Kilogramm Wasser weiter Energie zu! Die blaue Linie im Diagramm zeigt, dass dann
wieder die Temperatur steigt, wie es auch beim Eis unterhalb der Schmelztemperatur das Fall war.
Dass die blaue Linie steiler ansteigt als die rote, zeigt an, dass die spezifische Wärmekapazität
von flüssigem Wasser (also die Energie, die
einem Kilogramm flüssigem Wasser zugeführt werden muss, um ihn um
1 °C
zu erwärmen) höher ist als jene von Eis.
Sie hängt ein bisschen von der Temperatur ab und beträgt (bei Normaldruck) etwa
4200 J/(kg·K)
oder
4.2 kJ/(kg·K).
Genauer gesagt, variiert sie je nach Temperatur zwischen
4.18 kJ/(kg·K)
und
4.22 kJ/(kg·K).
Um unser Kilogramm Wasser von
0 °C auf
100 °C
zu erwärmen, ist daher eine Energie von etwa
100·4.2 kJ = 420 kJ
nötig. Umgekehrt lässt sich sagen, dass ein Kilogramm Wasser bei Abkühlung von
100 °C
bis zur Gefriertemperatur bei
0 °C
eine Energie von
420 kJ
abgibt.
- Die spezifische Wärmekapazität von flüssigem Wasser ist größer als die der meisten anderen Stoffe:
Eine hohe Energiezufuhr führt nur zu einer geringen Erwärmung.
Das bedeutet, dass Wasser ein sehr guter Wärmespeicher ist. Da die Ozeane hauptsächlich aus Wasser
bestehen, ist das auch für das Klima auf der Erde von Bedeutung.
- Was geschieht bei der Erwärmung von flüssigem Wasser?
Im flüssigen Aggregatzustand üben die Moleküle elektromagnetische Kräfte aufeinander aus,
sind aber, wie bereits erwähnt – im Gegensatz zum festen Aggregatzustand – nicht starr aneinander gebunden.
Ebenso wie im Festkörper befinden sie sich relativ dicht nebeneinander – ihr Abstand liegt in derselben Größenordnung wie ihre Größe.
Daher können sie sich nur über sehr kurze Strecken frei bewegen und stoßen
ständig aneinander. Diese Bewegungen werden bei fortgesetzter Energiezufuhr schneller, was sich als
Erwärmung, also als Temperaturanstieg äußert.
- Hat unser Kilogramm Wasser eine Temperatur von 100 °C
erreicht, so verdampft es, d.h. es geht in den gasförmigen Aggregatzustand über.
Die Temperatur, bei der dies passiert, ist für jeden Stoff charakteristisch (und hängt sehr stark vom Druck ab).
Sie wird Siedetemperatur (oder Verdampfungstemperatur) genannt.
Dem Diagramm entnehmen wir zwei wichtige Eigenschaften des Verdampfungsprozesses:
- Das Verdampfen vollzieht sich (bei Normaldruck) bei einer gleichbleibenden Temperatur von
100 °C.
Das bedeutet, dass
eine weitere Energiezufuhr zunächst nicht zu einer weiteren Erwärmung führt!
- Um unser Kilogramm Wasser (bei Normaldruck) vollständig zu verdampfen, ist eine sehr große Energiezufuhr nötig,
die so genannte Verdampfungswärme von
2257 kJ.
Sie ist fast sieben mal so groß wie die Schmelzwärme!
Verdampfen ist ein allmählicher Vorgang, bei dem flüssiges Wasser und gasförmiger Wasserdampf gleichzeitig existieren.
Je mehr Energie zugeführt wird, umso größer ist der Anteil des Wasserdampfes,
bis schließlich kein flüssiges Wasser mehr vorhanden ist. Mit dem Ende dieses Prozesses ist der Beginn
(d.h. das linke Ende) der grünen Linie erreicht.
- Die während des Verdampfens zugeführte Energie löst die Bindungen zwischen den Molekülen fast vollständig.
Im gasförmigen Zustand gibt es zwar noch Kräfte zwischen den Molekülen, aber sie sind erheblich kleiner
als die Kräfte, die im flüssigen Zustand wirken. In Gasen können sich die Moleküle über relativ lange
Strecken frei bewegen, bevor sie mit ihresgleichen zusammenstoßen. Daher füllt ein Gas
– im Gegensatz zu Festkörpern und Flüssigkeiten – den ihm zur Verfügung stehenden Raum aus
(sofern es nicht – wie unsere Atmosphäre – durch die Schwerkraft in Bodennähe gehalten wird).
- Das Verdampfen besitzt eine Umkehrung: das Kondensieren. Es tritt auf, wenn einem Gas Energie entzogen wird,
wenn in unserem Diagramm also von oben nach unten gegangen wird. Die Kondensationstemperatur ist gleich der Siedetemperatur.
Die Energie, die dem Wasserdampf entzogen werden muss, um ihn vollständig zu kondensieren (die Kondensationswärme) ist
gleich der Verdampfungswärme.
- Führen wir dem Wasserdampf weiter Energie zu, so steigt die Temperatur.
Der Anstieg der grünen Linie im Diagramm entspricht der spezifischen Wärmekapazität von Wasserdampf.
Sie
hängt ein bisschen von der Temperatur ab.
Im dargestellten Temperaturbereich liegt sie um
2 kJ/(kg·K), ist also ungefähr
gleich groß wie jene von Eis.
 - Volumina:

- Werden die angegebenen Werte für das Volumen, das unser Kilogramm Wasser in den verschiedenen
Aggregatzuständen (bei Normaldruck) annimmt, im Überblick betrachtet, so fällt sofort eines
auf: Ein Kilogramm Eis oder flüssiges Wasser hat ungefähr ein Volumen von
1 dm3,
während ein Kilogramm Wasserdampf bei
100 °C
ein 1700-mal so großes Raumgebiet ausfüllt!
Das bedeutet, dass jedem Molekül in 100 °C
heissem Wasserdampf ein Volumen zur Verfügung steht, das um den Faktor 1700 größer ist
als zuvor. Die Moleküle sind daher etwa 12 mal (dritte Wurzel aus 1700 !) so weit voneinander entfernt als im flüssigen Wasser oder
im Eis. Sie besitzen nun eine erheblich größere freie Weglänge – diese
Eigenschaft charakterisiert ganz allgemein ein Gas.
Die Zahlen für die Volumina auf dem Weg vom Eis zum Wasserdampf illustrieren sehr schön die
Auflösung des relativ dicht gepackten Molekülverbands beim Verdampfen.
Das kostet, wie der hohe Wert der Verdampfungswärme zeigt,
sehr viel Energie.
- Gehen wir die angezeigten Volumswerte, angefangen vom Eis bei
–40 °C, der Reihe nach durch:
Im festen Aggregatzustand nimmt das Volumen mit der steigender Temperatur leicht zu. Das ist das Phänomen der
Wärmeausdehnung. Wie kommt sie zustande? Wir haben bereits erwähnt, dass die Schwingungen der
Moleküle durch Energiezufuhr "stärker werden". "Stärkere Schwingungen" bedeutet aber nichts anderes,
als dass die Amplituden der Schwingungen größer werden, d.h. dass die Punkte,
um die die einzelnen Moleküle schwingen, auseinanderrücken. Die unmittelbare Folge ist eine Zunahme des
Volumens.
- Interessant ist der Übergang vom Eis zum flüssigen Wasser: Das Volumen wird beim Schmelzen ein bisschen kleiner.
In diesem Punkt verhält sich Wasser eher untypisch, da bei den meisten anderen Stoffen das Volumen beim
Schmelzen geringfügig zunimmt..
- Auch im flüssigen Aggregatzustand findet eine Wärmeausdehnung statt.
Lediglich in einem kleinen Temperaturbereich zwischen
0 °C
und
3.98 °C
zeigt Wasser eine Anomalie: Im Gegensatz zu anderen Flüssigkeiten nimmt das Volumen
mit steigender Temperatur ab (und zwar von
1.00016 dm3
auf
1.00003 dm3
– es handelt sich also um einen sehr kleinen Effekt).
Bei Temperaturen größer als
3.98 °C
verhält sich Wasser "normal", d.h. es dehnt sich mit zunehmender
Erwärmung aus.
- Auch unser Wasserdampf dehnt sich bei Erwärmung aus – prinzipiell kann das Volumen, das er beansprucht,
beliebig groß werden. Das ist eine allgemeine Eigenschaft von Gasen.
Um das richtig zu verstehen, ist es allerdings wichtig, zu bedenken, dass die Energiezufuhr während des von uns betrachteten Prozesses
stets bei konstantem Druck stattfindet.
Soll ein solcher Prozess für ein Gas experimentell realisiert werden, so muss man ihm die Gelegenheit geben, sein Volumen selbst zu wählen,
etwa indem man es bei konstant gehaltenem Luftdruck in einen Ballon einsperrt (dessen Kraft auf das Gas aber
vernachlässigbar klein sein soll).
Wird ein Gas hingegen in einen starren Behälter eingesperrt, so wird dadurch das Volumen festgehalten und
jegliche Wärmeausdehung von vornherein unterbunden.
- Die im Wasserdampf (wie in jedem Gas) enthaltene Energie steckt zum größten Teil in der Bewegungsenergie der Moleküle.
Kräfte zwischen den Molekülen, die mit (rechnerisch als negativ zu veranschlagenden) Bindungsenergien verbunden sind, sind zwar noch vorhanden,
spielen aber nur eine untergeordnete Rolle. Dementsprechend heizt weiterhin zugeführte Energie
direkt die Bewegung der Moleküle an. Aus diesem Grund sind die thermischen Eigenschaften von
Gasen berechenbarer als jene von Festkörpern und Flüssigkeiten und lassen sich
leichter erklären.
- Wir merken noch an, dass sich die Aggregatzustände auch hinsichtlich des Verhaltens unter variierendem Druck
voneinander unterscheiden:
Festkörper und Flüssigkeiten sind relativ "volumenbeständig", d.h. sie ändern ihr Volumen
nur geringfügig, wenn sie unter Druck gesetzt werden – sie lassen sich nicht leicht
komprimieren. Dieses Verhalten zeigt an, dass die Moleküle, die sich in diesen Aggregatzuständen ja
sozusagen unmittelbar nebeneinander befinden, sehr robust sind. Sie lassen sich nicht leicht "zusammendrücken" oder
"ineinander drücken".
Gase hingegen lassen sich leicht komprimieren – die Komprimierung eines Gases besteht lediglich
darin, die Abstände der Moleküle zu verkleinern.
 - Dichten:

- Die angezeigten Werte für die Dichten sind umgekehrt proportional zu den zuvor besprochenen
Werten für die Volumina.
- Die Wärmeausdehnung besteht darin, dass die Dichte mit zunehmender Temperatur abnimmt.
- Die Dichte von Eis ist kleiner als die Dichte von Wasser, was zur Folge hat, dass
Eis auf dem Wasser schwimmt – eine im Vergleich mit anderen Stoffen untypische Eigenschaft des Wassers.
- Die Dichten von Eis und flüssigem Wasser sind einander sehr ähnlich.
Generell liegen die Dichten der meisten Festkörper und Flüssigkeiten in einem überschaubaren Bereich
zwischen
500 kg/m3
und
20000 kg/m3.
Die Dichten von Gasen (bei Normaldruck) sind erheblich kleiner und übersteigen selten
3 kg/m3.
- Wird Wasserdampf erhitzt, so nimmt die Dichte ab – prinzipiell kann sie (wie bei jedem Gas)
beliebig klein werden.
- Die oben erwähnte Anomalie des Wassers zeigt sich auch an dessen Dichte
(und wird daher auch Dichteanomalie genannt): Die Dichte von flüssigem Wasser steigt zunächst von
999.85 kg/m3
bei
0 °C
auf
999.97 kg/m3
bei
3.98 °C
an und fällt bei höheren Temperaturen wieder ab.
Das hat zur Folge, dass im sehr kalten Wasser Schichten um die
4 °C absinken, während
die kälteren Schichten darauf schwimmen (und bei fortgesetztem Energieentzug gefrieren).
Dieses Phänomen kann Gewässer vor einem vollständigen Durchfrieren "von unten" während des Winters
schützen und ist daher wichtig für das Leben
in ihnen.
 - Vergleich Wasserdampf mit idealem Gas:

- Sind die Kräfte zwischen den Molekülen in einem Gas vernachlässigbar klein, und spielt auch ihre
Größe im Vergleich zu ihrem typischen Abstand keine Rolle, so lässt sich das Gas mit Hilfe eines
einfachen Modells beschreiben. Wir sprechen dann von einem idealen Gas.
- Der Anstieg der grünen Linie stellt, wie erwähnt, die
spezifische Wärmekapazität von Wasserdampf bei konstantem Druck dar.
Sie wird üblicherweise mit
cp
bezeichnet.
Der Anstieg der steilsten der drei grauen Linien entspricht der (theoretisch vorhergesagten)
spezifischen Wärmekapazität eines
idealen drei-atomigen Gases mit der gleichen molaren Masse wie Wasser
(nämlich 18 g/mol oder, um ganz genau zu sein,
18.01528 g/mol).
Sie ist fast parallel zur grünen Linie, was bedeutet, dass Wasserdampf recht gut als ideales drei-atomiges Gas
beschrieben werden kann.
-
Die Theorie dazu:

- Die in einem drei-atomigen idealen Gas steckende Bewegungsenergie teilt sich zu gleichen Anteilen in die
Energie der Translationsbewegung der Moleküle (3 Freiheitsgrade) und in die Energie der Rotation der Moleküle
(ebenfalls 3 Freiheitsgrade) auf.
Gemäß Boltzmanns berühmtem Äquipartitionstheorem (Gleichverteilungssatz)
fällt im Mittel auf jeden Freiheitsgrad eines Moleküls eine Bewegungsenergie
von k Tabs/2,
wobei k = 1.38·10–23 J/K
die Boltzmannkonstante und
Tabs
die absolute Temperatur ist
(Tabs, in K = Tin °C + 273.15).
Das ergibt für ein drei-atomiges ideales Gas insgesamt eine Bewegungsenergie von
3 k Tabs
pro Molekül.
- Wird dem Gas nun Energie zugeführt, so wird einerseits diese Bewegungsenergie erhöht.
Zusätzlich dehnt sich das Gas aus (wir halten ja den Druck konstant und müssen dem Gas daher die Gelegenheit
geben, sein Volumen selbst zu bestimmen), wobei es Expansionsarbeit verrichtet, und zwar im Ausmaß von
k ΔT
pro Molekül bei einer Erhöhung der Temperatur um
ΔT.
(Beachten Sie, dass
ΔTabs = ΔT,
da sich
Tabs
und
T
nur um eine additive Konstante unterscheiden).
Insgesamt muss dem Gas daher eine Energie zugeführt werden, die im Mittel
4 k ΔT
pro Molekül ausmacht, um einen Temperaturanstieg von
ΔT
zu erreichen. Genau diese benötigte Energie (multipliziert mit
3.3427·1025, der Zahl der Moleküle
pro Kilogramm unseres Gases) stellt der Anstieg der steilsten der drei grauen Linien dar. Er stimmt sehr gut mit dem Anstieg der grünen Linie
für den Wasserdampf überein.
Kleine Abweichungen dieses idealisierten Werts vom tatsächlich gemessenen
rühren daher, dass die Moleküle auch im gasförmigen Zustand (kleine) Kräfte aufeinander ausüben.
Bei sehr hohen Temperaturen (höher als den hier betrachteten) können auch die Schwingungen der Atome im Wassermolekül
eine gewisse Energiemenge aufnehmen, was ebenfalls eine Erhöhung der spezifischen Wärmekapazität
bewirkt.
- Die Anstiege der beiden anderen grauen Linien entsprechen ein- und zwei-atomigen Gasen mit der gleichen molaren Masse wie Wasser.
In einem ein-atomigen Gas, dessen Moleküke (= Atome) keine ins Gewicht fallenden Rotationsfreiheitsgrade besitzen, kommt auf ein Atom im Mittel eine Bewegungsenergie von
3 k Tabs/2,
in einem zwei-atomigen Gas, dessen Moleküle nur zwei relevante Rotationsfreiheitsgrade besitzen, kommt auf ein Molekül im Mittel eine Bewegungsenergie von
5 k Tabs/2.
Die Expansionsarbeit bei Erwärmung unter konstantem Druck ist die gleiche wie beim drei-atomigen Gas
(k ΔT pro Molekül), so dass diese
beiden grauen Linien eine Energiezufuhr von
5 k ΔT/2
bzw.
7 k ΔT/2
pro Molekül für eine Erhöhung der Temperatur um
ΔT
darstellen.

Manche interessanten Eigenschaften des Wassers und der Materie generell wurden hier nicht erwähnt:
- Hier wäre vor allem das aus der Alltagserfahrung bekannte Verdunsten zu nennen, bei dem einzelne
(besonders schnelle und daher energiereiche) Moleküle nahe einer Wasseroberfläche die von ihren
Nachbarn ausgeübten Anziehungskräfte (die sich auch durch die Oberflächenspannung zeigen)
überwinden und damit der Flüssigkeit entkommen.
Dieser Prozess findet (im Gegensatz zum Verdampfen) bei jeder Temperatur statt, auch ohne äußere Energiezufuhr.
Durch das Entfliehen der energiereichsten Moleküle wird der Flüssigkeit die Verdunstungswärme entzogen, was einem Kühleffekt gleichkommt
(der etwa auf nasser Haut deutlich gespürt wird).
Ein wichtiger Begriff in diesem Zusammenhang ist der Sättigungsdampfdruck, der sich ergibt, wenn
sich in einem Gefäß lediglich Wasser und Wasserdampf befinden und sich zwischen dem Verdunsten und dem
Wieder-Eintreten von Molekülen in die Flüssigkeit ein Gleichgewicht eingestellt hat.
- Weitere Phänomene sind das Sublimieren und das Resublimieren, d.h. der
direkte Übergang vom festen in den gasförmigen Zustand und umgekehrt.
- Werden andere Drücke als der Normaldruck von (etwas mehr als)
1 bar
zugelassen, so ändern sich die Verhältnisse teilweise dramatisch, wie das
(schematische und vereinfachte) Phasendiagramm der Gleichgewichtszustände des Wassers zeigt:
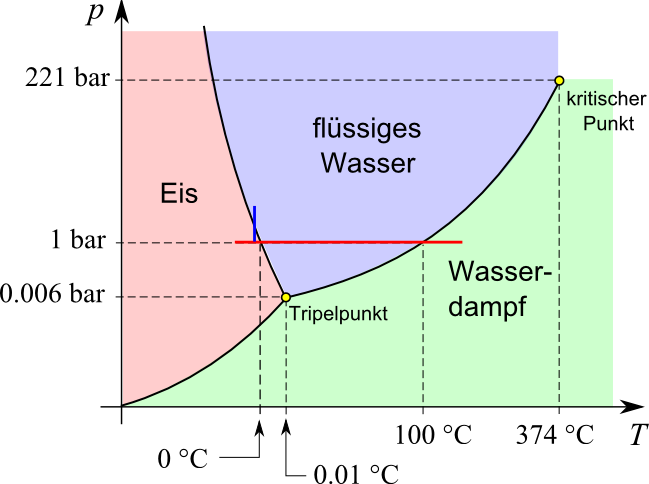
Die beim oben diskutierten Prozess vorkommenden Zustände liegen alle auf der roten Linie.
Verlassen wir sie, so treten neue Phänomene auf:
- Wie aus dem Diagramm hervorgeht, wird die Schmelztemperatur mit zunehmendem Druck kleiner (eine weitere Anomalie des
Wassers, da die Schmelztemperatur der meisten anderen Stoffe mit zunehmendem Druck steigt). Das hat zur Folge, dass Eis
bei gleichbleibender Temperatur nach einer Erhöhung des Drucks flüssig werden kann
(entsprechend der kurzen blauen Linie im Phasendiagramm)
– ein Effekt, der für das Fließen von Gletschern verantwortlich ist. Ob wir ihm auch – wie oft zu lesen ist –
die Möglichkeit des Schlittschuhlaufens verdanken, ist umstritten (siehe dazu
diese Seite).
- Unterhalb eines Drucks von
0.006 bar
existiert kein flüssiges Wasser.
- Beim Tripelpunkt können alle drei Aggregatzustände gleichzeitig existieren.
- Oberhalb des kritischen Punkts kann zwischer flüssigem und gasförmigem Aggregatzustand nicht mehr unterschieden werden,
da sich ihre Dichten einander annähern (der Zustand wird dann überkritisch genannt).
Unter noch extremeren Bedingungen ändern sich die Verhältnisse ein weiteres Mal. So ist in den letzten Jahrzehnten entdeckt worden,
dass Eis in Wahrheit zahlreiche unterschiedliche Aggregatzustände annehmen kann, deren Erklärung
durch die zwischen den Molekülen wirkenden Kräfte Gegenstand aktueller Forschung ist.
Nachbemerkung: In der Wärmelehre wird (vor allem im Zusammenhang mit ihrem "ersten Hauptsatz") von der
inneren Energie
U
eines Stoffes gesprochen. Sie umfasst sowohl die ungeordnete Bewegung der Moleküle
(Translations- und Rotationsenergien) als auch die Bindungsenergien. Sie ändert sich, wenn dem Stoff
(etwa durch den Kontakt mit einem ihn umgebenden Wärmebad) Wärmeenergie zu- oder abgeführt wird,
wenn an ihm mechanische Arbeit geleistet wird oder er mechanische Arbeit an seiner Umgebung leistet.
Daher wird viel von der Änderung ΔU
der inneren Energie gesprochen. Selten erfahren Sie aber – ausgenommen, es ist von idealen Gasen die Rede –,
wie groß die innere Energie insgesamt ist
(also ein U ohne
Δ). Das liegt zum Teil daran, dass
in einem Stoff Bindungsenergien enthalten sind, die in der Wärmelehre normalerweise
nicht betrachtet werden, z.B. die Bindungen der Kernbausteine (Nukleonen) aneinander durch die Kernkräfte.
Werden keine chemischen Umwandlungen betrachtet, so sind auch die Bindungsenergien, die die Atome zu
Molekülen verbinden, irrelevant. Es ist also gar nicht einfach zu sagen, wie groß "die innere Energie"
eines Stoffes nun eigentlich ist. Um aber dennoch einen Eindruck davon zu bekommen, legen wir als Vergleichszustand
jenen Zustand unseres Kilogramms Wasser jenen Zustand fest, in dem die einzelnen Wassermoleküle weit voneinander
getrennt sind und sich nicht bewegen. Wir ignorieren also chemische Energien und Kernenergien, die im
Wasser stecken. Ordnen wir einem solchen Zustand den Wert
U = 0 für die innere Energie zu,
so kann auf der senkrechten Achse unseres obigen Diagramms anstelle der ab dem Ausgangspunkt bei
–40 °C
hineingesteckten Energie E
die innere Energie
U
auftragen werden. Das Diagramm sieht dann so aus:

Eine gedachte Verlängerung der grünen Linie nach links schneidet dann die Temperaturachse beim
absoluten Nullpunkt, d.h. bei
–273.15 °C.
Lassen wir also chemische Reaktionen und Kernprozesse außer Acht, so ergibt sich folgendes Bild:
- Eis und flüssiges Wasser unter
100 °C
besitzen bei Normaldruck in thermodynamischer Hinsicht eine negative
innere Energie, d.h. es überwiegen die (negativ veranschlagten) Bindungsenergien über die
(positiven) kinetischen Energien der ungeordneten Wärmebewegung.
- Wasserdampf bei
Temperaturen über
100 °C
hingegen besitzt bei Normaldruck in thermodynamischer Hinsicht
eine positive innere Energie, d.h. hier können die
Wechselwirkungsenergien der Wassermoleküle in erster Näherung vernachlässigt werden
(was wiederum der Grund dafür ist, dass Wasserdampf recht gut als ideales Gas beschrieben werden kann).
- Das hat eine interessante Konsequenz: Würde unser Kilogramm Wasserdampf
bei einer Temperatur über
100 °C
in Schwerelosigkeit und ohne Gefäßwände sich selbst überlassen,
so könnte er sich in energetischer Hinsicht unbegrenzt verdünnen, d.h. seine Moleküle
könnten sich komplett voneinander lösen und in unterschiedliche Richtungen auseinanderfliegen.
Bei einem Zustand mit negativer innerer Energie (d.h.
unterhalb der Temperaturachse) wäre das nicht möglich. Ein im Weltall allein gelassener Eisbrocken
könnte zwar einzelne Moleküle durch Sublimierung verlieren, würde dadurch aber immer
kälter und damit fester gebunden.
|
