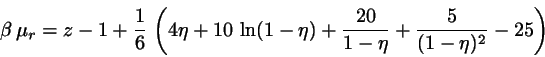

0.1 Widom's technique and Nezbeda-Kolafa's extension
The basic idea of the Widom test particle method is to try to insert, at
regular intervals, a particle at a random position. The particle
is assumed to have no influence on the rest of the system, but it has
an energy
 with respect to
the
with respect to
the  ``real'' particles. From
``real'' particles. From
![\begin{displaymath}
\exp[-\beta \mu_{r}] = \exp[-\beta (A_{N+1}-A_{N}) ] =
...
...N}\exp[-\beta U_{N}] }
= <\exp[-\beta \Delta U_{t}]>_{N}
\end{displaymath}](img3.png) |
(1) |
(with
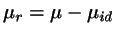 ) we conclude that
) we conclude that
![\begin{displaymath}
\exp[-\beta \mu]=Q_{id} <\exp[-\beta \Delta U_{t}]>_{N}
\end{displaymath}](img5.png) |
(2) |
In a MC or MD simulation, then, we periodically try to introduce a visiting
particle and register its Boltzmann factor
![$\exp[-\beta \Delta U_{t}]$](img6.png) for averaging.
for averaging.
Evidently, in a dense system the addition of another particle at a random
position will result in a very low Boltzmann factor of that particle. Thus
a lot of almost-zeroes will be added up for averaging.
A gradual insertion, or ``staging'' (Kofke) method may help to improve
the efficiency. The first implementation of such a technique is due to
Mon and Griffiths (1985).
In Nezbeda and Kolafa's work (1991) this older version is dubbed
``method A'' while their own modification is called method B.
Method A:
Write the ratio
 as
as
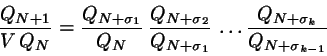 |
(3) |
where
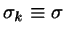 and
and
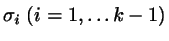 pertains to an intermediate state of a scaled particle. Thus
pertains to an intermediate state of a scaled particle. Thus
![\begin{displaymath}
\frac{Q_{N+1}}{V Q_{N}} =
<\exp[-\beta \Delta U_{N+\sig...
...\sigma_{i}}]>_{N+\sigma_{i}}
= q_{0} \prod_{i=1}^{k-1} q_{i}
\end{displaymath}](img11.png) |
(4) |
In method A each of the factors
![$<\exp[-\beta \Delta U_{N+\sigma_{i+1}}-U_{N+\sigma_{i}}]>_{N+\sigma_{i}}$](img12.png) is determined in a separate simulation, so that
is determined in a separate simulation, so that 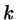 simulations are needed
to arrive at an estimate of
simulations are needed
to arrive at an estimate of 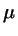 .
.
Method B:
Nezbeda and Kolafa suggested that one long MC run be used to sample all
intermediate and final states of the generalized ensemble made up of
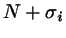 particles. The tentative growing or shrinking of a particle
is then just another one of the MC trial steps. Assigning weights
particles. The tentative growing or shrinking of a particle
is then just another one of the MC trial steps. Assigning weights 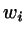 to the various sub-ensembles, the Monte Carlo transition probability
is
to the various sub-ensembles, the Monte Carlo transition probability
is
![\begin{displaymath}
P_{i \rightarrow j} =
{\rm min} \left\{ 1, \frac{p_{ij}}{p...
...w_{j} \exp[-\beta U_{j}]}{w_{i} \exp[-\beta U_{i}]}\right\}
\end{displaymath}](img17.png) |
(5) |
where the 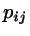 (
(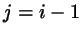 or
or  ) are the a priori trial
probabilities for growing and shrinking. The optimal choice for
the weights
) are the a priori trial
probabilities for growing and shrinking. The optimal choice for
the weights 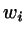 and
and 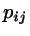 are considered below.
are considered below.
The residual chemical potential is given by
![\begin{displaymath}
\beta \mu_{r} = \ln \left[ w_{k} Pr(N)/Pr(N+1)\right]
\end{displaymath}](img21.png) |
(6) |
with 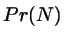 the probability (or relative frequency) of state
the probability (or relative frequency) of state  in the
semi-grand ensemble spanned by all states of the systems
in the
semi-grand ensemble spanned by all states of the systems
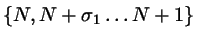 .
.
Method C: As a further generalization, Nezbeda and Kolafa consider
the grand canonical ensemble spanned by
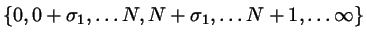 .
We will not treat this any further.
.
We will not treat this any further.
Optimal parameters:
The growing of particles by one size stage should be equally probable
for all  . Taking hard spheres as an example, the chemical potential for
. Taking hard spheres as an example, the chemical potential for
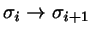 is approximately proportial to
is approximately proportial to
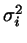 . Therefore, the hard sphere diameter should be
discretized according to
. Therefore, the hard sphere diameter should be
discretized according to
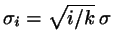 . Other
coupling parameters than the particle diameter may be treated in a similar
way.
. Other
coupling parameters than the particle diameter may be treated in a similar
way.
The best choice for the weights 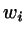 is
is
![$w_{i+1}/w_{i}=\exp[\beta \mu_{r}/k]$](img29.png) .
.
For best performance, the trial probabilities 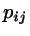 should be such
that
should be such
that
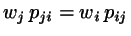 (see 5).
For the first stage,
(see 5).
For the first stage,
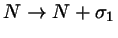 we take this probability
as
we take this probability
as 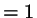 , and for the intermediate steps
, and for the intermediate steps
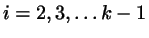 we have
we have
![$p_{i,i+1}=1-p_{i-1,i} \exp[-\beta \mu_{r}/k]$](img34.png) .
At the final step,
there is no further growth, and the non-change is tried with probability
.
At the final step,
there is no further growth, and the non-change is tried with probability
![$p_{N+1,N+1} = 1-p_{N+\sigma_{k-1},N+1}\exp[-\beta \mu_{r}/k]$](img35.png) .
At all stages, the sum of the two trial probabilities equals
.
At all stages, the sum of the two trial probabilities equals  .
(In the grand canonical method C, the rules are slightly more symmetric,
since a growth beyond
.
(In the grand canonical method C, the rules are slightly more symmetric,
since a growth beyond 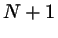 and a shrinkage below
and a shrinkage below  is permitted.)
is permitted.)
Test of the method by Nezbeda/Kolafa:
These authors chose a HS fluid as their test sample. The chemical
potential in this case may be calculated explicitely by integrating the
Carnahan-Starling formula:
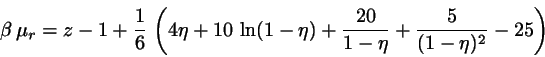 |
(7) |
with
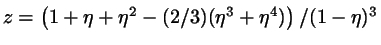 .
Thus the simulation results may be checked against (semi-)exact theory.
.
Thus the simulation results may be checked against (semi-)exact theory.
[to be extended...]

 F. J. Vesely / University of Vienna
F. J. Vesely / University of Vienna
![\begin{displaymath}
\exp[-\beta \mu_{r}] = \exp[-\beta (A_{N+1}-A_{N}) ] =
...
...N}\exp[-\beta U_{N}] }
= <\exp[-\beta \Delta U_{t}]>_{N}
\end{displaymath}](img3.png)
![\begin{displaymath}
\exp[-\beta \mu_{r}] = \exp[-\beta (A_{N+1}-A_{N}) ] =
...
...N}\exp[-\beta U_{N}] }
= <\exp[-\beta \Delta U_{t}]>_{N}
\end{displaymath}](img3.png)
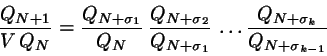
![\begin{displaymath}
\frac{Q_{N+1}}{V Q_{N}} =
<\exp[-\beta \Delta U_{N+\sig...
...\sigma_{i}}]>_{N+\sigma_{i}}
= q_{0} \prod_{i=1}^{k-1} q_{i}
\end{displaymath}](img11.png)