
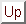

Among the excluded volumes discussed in the text are bodies
- cylinders, truncates spheres or ellipsoids - that are capped
by sphere segments. Let such a cap have its center at 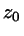 , its
rim at
, its
rim at 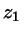 , and a radius
, and a radius 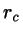 . The cosine integral over one
such end cap is then given by
. The cosine integral over one
such end cap is then given by
where

 F. J. Vesely / University of Vienna
F. J. Vesely / University of Vienna
![$\displaystyle \int_{z_{1}}^{z_{0}+r_{c}}
dz \, \left[r_{c}^{2}-\left(z-z_{0} \right)^{2} \right] \, \cos kz$](img128.png)
![$\displaystyle \pi \, \cos kz_{0} \left\{
\frac{}{} \right. \left. \!\!
\frac{r_{c}^{2}}{k}\, \left[
\sin k(z_{1}-z_{0}+r_{c})-\sin k(z_{1}-z_{0}\right]
\right.$](img129.png)
![$\displaystyle \hspace{9em} \left.
-\left[ f(z_{1}-z_{0}+r_{c};k) - f(z_{1}-z_{0};k) \right]
\frac{}{}
\right\}$](img130.png)
![$\displaystyle -\pi \, \sin kz_{0} \left\{
\frac{}{} \right. \left. \!\!
- \frac...
...c}^{2}}{k}\, \left[
\cos k(z_{1}-z_{0}+r_{c})-\cos k(z_{1}-z_{0}\right]
\right.$](img131.png)
![$\displaystyle \int_{z_{1}}^{z_{0}+r_{c}}
dz \, \left[r_{c}^{2}-\left(z-z_{0} \right)^{2} \right] \, \cos kz$](img128.png)
![$\displaystyle \pi \, \cos kz_{0} \left\{
\frac{}{} \right. \left. \!\!
\frac{r_{c}^{2}}{k}\, \left[
\sin k(z_{1}-z_{0}+r_{c})-\sin k(z_{1}-z_{0}\right]
\right.$](img129.png)
![$\displaystyle \hspace{9em} \left.
-\left[ f(z_{1}-z_{0}+r_{c};k) - f(z_{1}-z_{0};k) \right]
\frac{}{}
\right\}$](img130.png)
![$\displaystyle -\pi \, \sin kz_{0} \left\{
\frac{}{} \right. \left. \!\!
- \frac...
...c}^{2}}{k}\, \left[
\cos k(z_{1}-z_{0}+r_{c})-\cos k(z_{1}-z_{0}\right]
\right.$](img131.png)
![$\displaystyle \int_{0}^{x}dz \, z^{2} \, \cos kz
= \frac{1}{k^{3}}\left[ 2kx \cos kx + \left( (kx)^{2}-2\right) \sin kx\right]$](img134.png)
![$\displaystyle \int_{0}^{x}dz \, z^{2} \, \sin kz
= \frac{1}{k^{3}}\left[ 2kx \sin kx - \left( (kx)^{2}-2\right) \cos kx
-2 \right]$](img136.png)