

Here we recount the second virial approximation of Koda et al. in
a format that lends itself easily to a generalisation to other
mixtures than the spherocylinder/sphere system. In particular, the following
relations are valid for any kind of hard linear particles with
cylindrical and inversion symmetry.
Let
 ,
,
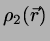 denote the local number
densities of two species of hard particles, with
denote the local number
densities of two species of hard particles, with
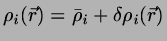 where
where
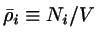 .
The free energy of the mixture at the level of the second virial
approximation is
.
The free energy of the mixture at the level of the second virial
approximation is
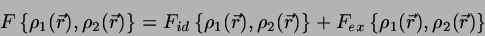 |
(13) |
with
![\begin{displaymath}
\frac{1}{kT}F_{id}\left\{...\right\} =
\sum_{i=1}^{2}\int d\...
...ambda_{i} +
\rho_{i}(\vec{r}) \, \ln \rho_{i}(\vec{r})\right]
\end{displaymath}](img94.png) |
(14) |
and
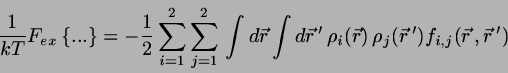 |
(15) |
where
 is the Mayer overlap function for a pair of particles at the given positions.
Since we are dealing with hard particles,
is the Mayer overlap function for a pair of particles at the given positions.
Since we are dealing with hard particles, 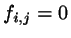 except for the
overlap region of the two objects, where
except for the
overlap region of the two objects, where 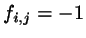 .
.
The local density variations
 produce
a free energy difference with respect to the homogeneous density system.
produce
a free energy difference with respect to the homogeneous density system.
Ideal free energy:
The ideal part of the free energy variation per particle is given by
To study the possible onset of a nematic-smectic transition a periodic
density variation
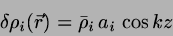 |
(18) |
is assumed and inserted in ![[*]](crossref.png) . For the term quadratic in
. For the term quadratic in
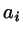 , we have
, we have
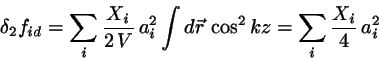 |
(19) |
with
 .
Thus
.
Thus
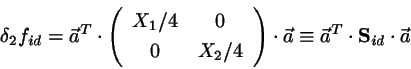 |
(20) |
where
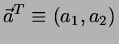 , and
, and
 is the ideal part of the stability matrix.
is the ideal part of the stability matrix.
Excess free energy:
From ![[*]](crossref.png) and
and ![[*]](crossref.png) we have
we have
 |
(21) |
with the overlap integral defined as
 |
(22) |
where
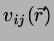 denotes the excluded volume centered at
denotes the excluded volume centered at 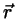 .
For linear particles symmetric with respect to
.
For linear particles symmetric with respect to
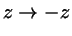 the general overlap integral may be simplified as
the general overlap integral may be simplified as
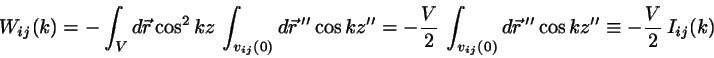 |
(23) |
where 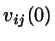 is now centered at the origin.
is now centered at the origin.
Thus the central task in this approach is the calculation of the cosine
transform of the three kinds of excluded volumes,
 |
(24) |
For the quadratic term in the expression for the excess free energy density
we have
 ,
where the matrix elements of
,
where the matrix elements of
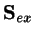 are
are
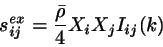 |
(25) |
It is convenient here to introduce the volume of the linear particles
and relate it to the volume of the hard spheres, thus:
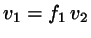 . Using the total packing fraction
. Using the total packing fraction 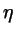 in place of
in place of 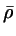 we have
we have
![\begin{displaymath}
s_{ij}^{ex} =
\frac{1}{4}
\frac{\eta}{\left[ (1-X_{sp})f_{lb}+X_{sp}\right]}
X_{i} X_{j} \frac{I_{ij}(k)}{v_{2}}
\end{displaymath}](img121.png) |
(26) |
This is a general result valid for hard particles having cylindrical and
inversion symmetry (
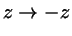 ) mixed with hard spheres.
Specific systems made up of
spherocylinders/spheres, ellipsoids/spheres, and fused spheres/spheres
will be considered below. Also, a mixture of ``spheroellipsoids''
and spheres is studied.
) mixed with hard spheres.
Specific systems made up of
spherocylinders/spheres, ellipsoids/spheres, and fused spheres/spheres
will be considered below. Also, a mixture of ``spheroellipsoids''
and spheres is studied.
The total stability matrix is just
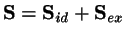 .
The system will become unstable towards smectic demixing if at the
given densities there exists a wave number
.
The system will become unstable towards smectic demixing if at the
given densities there exists a wave number 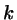 for which the determinant
for which the determinant
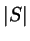 becomes zero. An eventual smectic phase will be stable if
becomes zero. An eventual smectic phase will be stable if
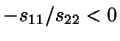 .
.

 F. J. Vesely / University of Vienna
F. J. Vesely / University of Vienna
![]() ,
,
![]() denote the local number
densities of two species of hard particles, with
denote the local number
densities of two species of hard particles, with
![]() where
where
![]() .
The free energy of the mixture at the level of the second virial
approximation is
.
The free energy of the mixture at the level of the second virial
approximation is
![\begin{displaymath}
\frac{1}{kT}F_{id}\left\{...\right\} =
\sum_{i=1}^{2}\int d\...
...ambda_{i} +
\rho_{i}(\vec{r}) \, \ln \rho_{i}(\vec{r})\right]
\end{displaymath}](img94.png)
![]() produce
a free energy difference with respect to the homogeneous density system.
produce
a free energy difference with respect to the homogeneous density system.
![[*]](crossref.png) . For the term quadratic in
. For the term quadratic in
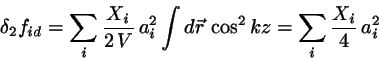
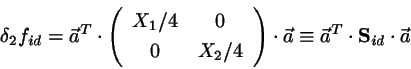
![[*]](crossref.png) and
and ![[*]](crossref.png) we have
we have


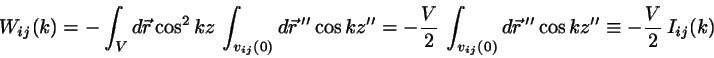
![]() .
The system will become unstable towards smectic demixing if at the
given densities there exists a wave number
.
The system will become unstable towards smectic demixing if at the
given densities there exists a wave number ![]() for which the determinant
for which the determinant
![]() becomes zero. An eventual smectic phase will be stable if
becomes zero. An eventual smectic phase will be stable if
![]() .
.
 Applet Koda_sc:
Start
Applet Koda_sc:
Start