| Franz J. Vesely > Square Well Line Mixture |
|
||||
Square Well Line MixtureConsider two lines of finite lengths $L_{1,2} = 2h_{1,2}$ containing a homogeneous density of square well centers. Let $\vec{r}_{1,2}$ and $\vec{e}_{1,2}$ be the position and direction vectors, respectively, of the two line centers, and write $\vec{r}_{12}$ for the vector between the centers; let $\lambda, \, \mu$ be the parameters giving the positions of the interacting points along $1$ and $2$. The squared distance between any two such points is given by $r^{2}= \left | r_{12}+\mu \cdot \vec{e}_{2}-\lambda \cdot \vec{e}_{1} \right|^{2} $. The total interaction energy between the two lines is then
$
u(1,2) \equiv u(\vec{r}_{12},\vec{e}_{1},\vec{e}_{2}) =
\frac{\textstyle 1}{\textstyle L_{1} L_{2}}
\int \limits_{\textstyle -h_{1}}^{\textstyle h_{1}} d \lambda
\int \limits_{\textstyle -h_{2}}^{\textstyle h_{2}} d \mu \, \,
u_{SW}\left[ r(\lambda,\mu) \right]
$
with $u_{SW}(r)= \infty $ if $r < s_{1}$, $= - \varepsilon $ if $s_{1} < r < s_{2}$, and $=0$ for $r > s_{2}$. Typically, $s_{1}=1.0$ and $s_{2}=1.5 - 2.0$. The elementary distance $r(\lambda,\mu)$ is $r^{2}= \lambda^{2}+\mu^{2} + 2 \mu b - 2 \lambda c - 2 \lambda \mu d + r_{12}^{2}$, where $b=\vec{r}_{12} \cdot \vec{e}_{2}$, $c=\vec{r}_{12} \cdot \vec{e}_{1}$, and $d=\vec{e}_{1} \cdot \vec{e}_{2}$. Note that we can always enforce $d > 0$ by simply turning $\vec{e}_{2}$ around; all parameters remain the same, except $b$ which changes sign. In the $(\lambda, \mu )$ plane the integration region is represented by a rectangle $R_{0}$ with sides $L_{1,2}$ around $(0,0)$. However, the integrand is non-zero, and constant, only for $ r^{2}(\lambda, \mu ) < s_{2}^{2}$. In other words, the integral gives the area shared by the rectangle $R_{0}$ and an ellipse $E$ described by $\lambda^{2}+\mu^{2} + 2 \mu b - 2 \lambda c - 2 \lambda \mu d - a^{2} =0$ where $a^{2}=s_{2}^{2}-r_{12}^{2}$.
Since this overlap region must be within the smallest rectangle $R_{E}$ containing the ellipse, only the - generally rectangular - section $R_{2} \equiv R_{0} \cap R_{E}$ needs to be considered; see Fig. 1. 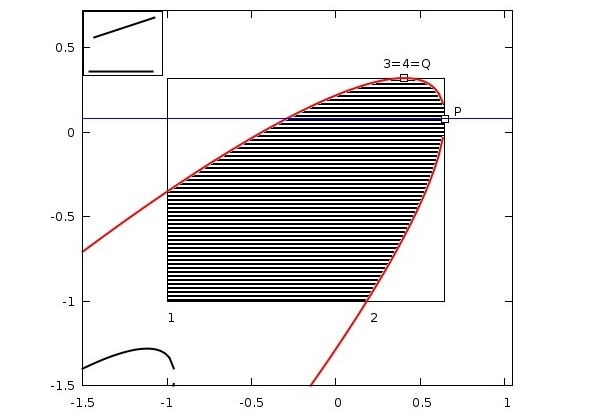
Figure 1: Square well lines in 2D, for $L_{1}=L_{2}=2 $, $s_{2}=1.5$. The inset shows the configuration represented in the $\lambda, \mu$ plane. The potential is given by the overlap area of rectangle (in this case, square) and ellipse. The figure refers to the pair $\vec{r}_{12} = (0.1 | 1.4), \vec{e}_{1} = (1 | 0), \vec{e}_{2} = (0.95 | 0.312)$; the potential is $u=-1.5822/4= -0.39566$; numerical integration yields $-0.39554$. The smaller ellipse (in black) shows the region of hard body overlap; if this ellipse exists, i.e. has real points, it must not intersect the basic integration rectangle $R_{0}$ (see text). We have not made any reference to the dimension in which the SW lines reside, even if Fig. 1 shows a 2D example. In fact, the procedure of calculating the pair potential is the same for coplanar (2D) and skew (3D) lines. Here is a lengthy explanation how to compute the potential A short recipe follows below. The task of computing the common area of an ellipse and a rectangle may seem trivial, but we have to define a procedure that comprises all possible configurations of the interacting sticks, and thus of $E$ and $R_{0}$. First we make sure that the SW particles have no overlap, i.e. contain no points with a mutual distance below $s_{1}$. In other words, the rectangle $R_{0}$ must not intersect the smaller concentric ellipse. A proven method for assessing the minimum distance btw two sticks is due to Allen et al., Adv. Chem. Phys. Vol. LXXXVI, 1993, p.1.; see also here. Next, we find the points of minimum distance along the two carrier lines. (For coplanar lines these points coincide in the intersection, if any, of the two lines.) Assuming that the lines are not parallel, i.e. $d^{2} \neq 1$, these "proxy points" have the line parameters $\lambda_{0} = (c-bd)/(1-d^{2})$, $\mu_{0}=(cd-b)/(1-d^{2})$. If $d^{2}=1$, the sticks may be either in an end-to-end configuration, meaning that the carrier lines 1 and 2 are identical, or they are on parallel lines. In both such cases the parameters $\lambda_{0},\mu_{0},$ cannot, and need not, be calculated (see below.) Since $d \equiv \vec{e}_{1} \cdot \vec{e}_{2} \geq 0$ (which should be enforced, if need be, by $\vec{e_{2}} \rightarrow - \vec{e_{2}}$, resulting in $b \rightarrow -b$) the long axis of the ellipse is oriented along the main diagonal. The ellipse center is at $\lambda_{0} = (c-bd)/(1-d^{2})$ $\mu_{0}=(cd-b)/(1-d^{2})$. Note: To avoid the spurious singularity at $d^{2}=1$ we do not compute the full $\lambda_{0}, \mu_{0}$ but only their numerators $c-bd$ and $cd-b$, which is sufficient to determine the quadrant. For later reference we write the explicit form of $E$ as
$
\mu^{\pm}(\lambda) =
\lambda d - b \pm \sqrt{A \lambda^{2} + 2B \lambda +C}
$
where $A = - (1-d^{2})$, $B = c-bd$, $C = a^{2}+b^{2}$, and where the signs $\pm$ denote the upper and lower branches, respectively, of the ellipse. Alternatively, $E$ may be written as
$
\lambda^{\pm}(\mu) =
\mu d + c \pm \sqrt{F \mu^{2} + 2G \mu +H}
$
where $F=A = - (1-d^{2})$, $G = cd-b$, $H = a^{2}+c^{2}$, and where the signs $\pm$ denote the right and left branches, respectively, of the ellipse. To find the container rectangle $R_{E}$ we have to determine the left- and rightmost points $N$ and $P$, as well as the lowest and uppermost points $O$ and $Q$ of the ellipse. Now, since $\lambda_{N,P}= (B \mp \sqrt{B^{2}-AC})/(1-d^{2})$ and $\mu_{O,Q}=(G \mp \sqrt{G^{2}-FH})/(1-d^{2})$ there is again the danger of a singularity. But actually we need the points $N,O,P,Q$ only if they are within the rectangle $R_{0}$, and thus finite, meaning that in the case $d^{2}=1$ these points need not be determined at all. All we have to do is compare $\lambda_{P}(1-d^{2})$ to $h_{1}(1-d^{2})$, $\mu_{Q} (1-d^{2})$ to $h_{2}(1-d^{2})$, and similar for points $N$ and $O$. In this way we find the limits of the clipped rectangle $R_{2} \equiv R_{0} \cap R_{E}$ according to $\lambda_{l}'=\max (-h_{1} \, , \, \lambda_{N})$, $\lambda_{u}'=\min (h_{1} \, , \, \lambda_{P})$, $\mu_{l}=\max (-h_{2} \, , \, \mu_{O})$, $\mu_{u}=\min (h_{2} \, , \, \mu_{Q})$. Actually, the relevant integration limits $\lambda_{l,u}'$ may be reduced even further, which is why we have adorned them with an apostrophe. Consider the intersection points $1$ and $2$ of the lower rectangle side with the ellipse $E$ (see Figure 1.): let $\lambda_{1},\lambda_{2}$ be the left/right intersection of the lower side $\mu=\mu_{l}$ of $R_{2}$ with $E$; if such an intersection point is outside the limits ($\lambda_{l}, \lambda_{u}$), it is placed at the near end of that side:
$
\begin{eqnarray}
\lambda_{1,2} &=&
\min \left(\lambda_{u}',\max \left( \lambda_{l}',(\mu_{l}d+c)
\mp \sqrt{F \mu_{l}^{2}+2G \mu_{l}+H} \right) \right)
\end{eqnarray}
$
Similarly, we find the intersections between the upper rectangle side and $E$: let $\lambda_{3,4}$ be the left/right intersection of the upper side ($\mu=\mu_{u}$) of $R_{2}$ with $E$; if such an intersection point is outside the limits ($\lambda_{l}, \lambda_{u}$), it is placed at the near end of that side:
$
\begin{eqnarray}
\lambda_{3,4}=
\min \left(\lambda_{u}',\max \left(\lambda_{l}',(\mu_{u}d+c)
\mp \sqrt{F\mu_{u}^{2}+2G\mu_{u}+H} \right) \right)
\end{eqnarray}
$
Obviously, the portion of $E$ lying between $\lambda_{1}$ and $\lambda_{2}$ has a bottom part that extends below the limits of $R_{2}$ and will therefore be cut away. Now, in case $\mu_{l} > \mu_{P}$, with $\mu_{P} (1-d^{2}) = G + d \sqrt{B^{2}-AC}$, the point $2$ is on the upper branch of $E$, meaning that any point right of $2$ is also below $\mu_{l}$ and thus outside the interaction area. In other words, if $\mu_{l} > \mu_{P}$ the rectangle may be clipped down to $\lambda_{u}=\lambda_{2}$. A similar argument holds for point $1$ which may be lower than $\mu_{N} = (G - d \sqrt{B^{2}-AC})/ (1-d^{2})$, thus leading to a new lower integration limit $\lambda_{l}=\lambda_{1}$. Pursuing the same idea for the intersection points $3$ and $4$ of the upper rectangle side with $E$ we finally have
if $\mu_{l} > \mu_{P} \; \Rightarrow \; \lambda_{u}=\lambda_{2}$,
if $\mu_{u} < \mu_{P} \; \Rightarrow \; \lambda_{u}=\lambda_{4}$,
if $\mu_{l} > \mu_{N} \; \Rightarrow \; \lambda_{l}=\lambda_{1}$, if $\mu_{u} < \mu_{N} \; \Rightarrow \; \lambda_{l}=\lambda_{3}$ which completes the clipping of the container rectangle. The rest is easy: integrate the ellipse $E$ between the lower and upper limits, then clip off what is sticking out above and below $R_{2}$, thus:
$
A =
\int \limits_{\textstyle \lambda_{l}}^{\textstyle \lambda_{u}}
(\mu^{+}(\lambda)-\mu^{-}(\lambda) )
+ \int \limits_{\textstyle \lambda_{1}}^{\textstyle \lambda_{2}}
(\mu^{-}(\lambda)-\mu_{l} )
- \int \limits_{\textstyle \lambda_{3}}^{\textstyle \lambda_{4}}
(\mu^{+}(\lambda)-\mu_{u} )
\equiv
I_{0} + I_{12}^{-} - I_{34}^{+}
$
For the individual integrals we have
$
\begin{eqnarray}
I_{0} & \equiv &
2 \, \int \limits_{\textstyle \lambda_{l}}^{\textstyle \lambda_{u}}
d \lambda \,
\sqrt{A \lambda^{2}+2 B \lambda + C }
= J_{lu}
\\
I_{12}^{-} & \equiv &
\int \limits_{\textstyle \lambda_{1}}^{\textstyle \lambda_{2}}
d \lambda \,
\left[
\left( \lambda d - b - \mu_{l} \right)
- \sqrt{A \lambda^{2}+2 B \lambda + C }
\right]
=
\frac{\textstyle d}{\textstyle 2 }
\left( \lambda_{2}^{2}-\lambda_{1}^{2} \right)
- \left( b + \mu_{l} \right) \left(\lambda_{2}-\lambda_{1} \right)
- J_{12}
\\
I_{34}^{+} & \equiv &
\int \limits_{\textstyle \lambda_{3}}^{\textstyle \lambda_{4}}
d \lambda \,
\left[
\left( \lambda d - b - \mu_{u} \right)
+ \sqrt{A \lambda^{2}+2 B \lambda + C }
\right]
=
\frac{\textstyle d}{\textstyle 2 }
\left( \lambda_{4}^{2}-\lambda_{3}^{} \right)
- \left( b + \mu_{u} \right) \left(\lambda_{4}-\lambda_{3} \right)
+ J_{34}
\\
{\rm with} && \\
J_{ab} & = &
\frac{\textstyle 1}{\textstyle 2 A}
\left[
\left( A \lambda + B \right) \sqrt{A \lambda^{2}+2 B \lambda + C }
+ \frac{ \textstyle B^{2} - AC }{\textstyle \sqrt{-A}}
\arcsin \frac{\textstyle B + A \lambda}{\sqrt{B^{2}-AC}}
\right]_{\textstyle \lambda_{a}}^{\textstyle \lambda_{b}}
\end{eqnarray}
$
Franz Vesely, Oct 28, 2010 |