| Franz J. Vesely > CompPhys Tutorial > Selected Applications > Long Ranged Potentials |
6.5 Particles and FieldsIn many cases the interparticle potential may be safely neglected beyond a few particle diameters. Defining a cutoff distance $r_{co}$, we may estimate the importance of the neglected "tail" of a potential $u(r)$ by
$
\int \limits_{\textstyle r_{co}}^{ \infty} u(r) 4 \pi r^{2} dr
$
If the decay of $u(r)$ is slow, this integral may be non-negligible. For example, the interaction between charged particles decays only as $r^{-1}$, and any cutoff will introduce a considerable error. Another instance is astrophysics, where the gravitational potential reaches too far to permit a simple cutoff. For ionic systems that are globally neutral the Ewald summation method known from solid state physics may be invoked. In the case of hot plasmas or gravitating systems the Particle-Mesh methods are appropriate. Subsections 6.5.1 Ewald summationLet
$
u_{qq}=\frac{\textstyle q_{1}q_{2}}{\textstyle r}
$
be the ion-ion interaction between charged particles. In the Ewald summation approach the basic cell containing $N/2$ each of positive and negative charges in some spatial arrangement is interpreted as a single crystallographic element surrounded by an infinite number of identical copies of itself. The entire system is then neutral and contains an infinite number of charges situated at points $ r_{j+}$ and $r_{j-}$, respectively. The total potential at the position of some ion $i$ residing in the basic cell is given by the finite difference of two infinite, diverging series:
$
\phi( r_{i})=
q \sum \limits_{j+}^{\infty}
\frac{\textstyle 1}{\textstyle | r_{i}- r_{j+} |} -
q \sum \limits_{j-}^{\infty}
\frac{\textstyle 1}{\textstyle | r_{i}- r_{j-} | }
$
We are facing the problem of an undetermined form $\infty - \infty$. Instead of evaluating the potential as a sum over the point charges we may first rewrite these charges as delta-like charge densities,
$
\rho( r)=
q \sum \limits_{j+}^{\infty} \delta \left( r- r_{j+} \right) -
q \sum \limits_{j-}^{\infty} \delta \left( r- r_{j-} \right)
$
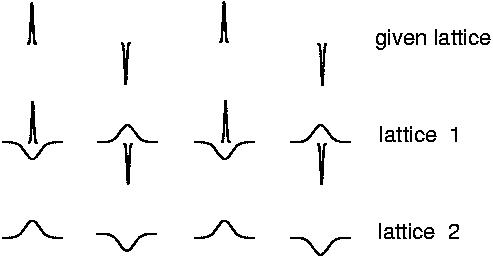
and expand these in a Fourier series whose terms determine the Fourier components $\phi( k)$ of the electrostatic potential. Since the Fourier representation of a delta-function requires infinitely many terms, the Fourier space calculation would again lead to convergence problems. The solution is to split up the potential in two well-behaved parts, one being represented in $r$-space and the other in $k$-space by rapidly converging series. We demonstrate this on a one-dimensional ion lattice with a charge distribution as depicted in Figure 6.8.
Figure 6.8: Ewald summation
We augment the delta-like point charges by Gaussian charge "clouds" of opposite sign,
$
\rho'(r) = -q_{j}\left(\frac{\textstyle \eta^{2}}{\textstyle \pi} \right)^{3/2}
e^{\textstyle - \eta^{2}( r- r_{j})^{2}}
$
(6.11)
to form an auxiliary lattice $1$. A further lattice ($2$) is then introduced
to compensate the additional Gaussian charges, such that
"lattice 1 + lattice 2 = original lattice".
The contributions of the two lattices to the potential are computed separately:
Proceeding to three-dimensional model systems, we consider a cubic base cell with side length $L$ containing $N$ charges. Fourier vectors:
$
k \equiv \frac{\textstyle 2 \pi}{\textstyle L} \left( k_{x}, k_{y}, k_{z}\right)
$
with integer $k_{x}$ etc. Interparticle vectors: including all periodic images of the base cell, we have
$
r_{i,j, n} \equiv r_{j} + n L - r_{i}
\;\;\; (i,j = 1, \dots, N)
$
where $nL$ is a translation vector in the periodic lattice. Ewald sum:
$
\phi \left(r_{i}\right) = \frac{\textstyle 4 \pi}{\textstyle L^{3}}
\sum \limits_{j}^{N} q_{j} \left[
\sum \limits_{ k} e^{\textstyle -i k \cdot r_{ij}}
k^{-2} e^{\textstyle -k^{2}/ 4 \eta^{2}} +
\sum \limits_{ n} F(\eta | r_{i,j, n}| ) \right]
$
with
$
F(z) \equiv \frac{\textstyle 2}{\textstyle \sqrt{\pi}}
\int_{z}^{\infty} e^{\textstyle -t^{2}} dt
$
Note: Two details need attention:
Considering these two corrections, we have for the total
potential energy
$
E_{pot} = \frac{\textstyle 1}{\textstyle 2}
\sum \limits_{i}^{N} q_{i} \phi \left( r_{i}\right)
- \frac{\textstyle \eta}{\textstyle \sqrt{\pi}}
\sum \limits_{i}^{N}q_{i}^{2}
+\frac{\textstyle 2 \pi}{\textstyle 3L^{3}}
| \sum \limits_{i}^{N} q_{i} r_{i} |^{2}
$
Another interesting class of particles are those with embedded point dipoles. Several methods have been devised to deal with the long range contributions in these model systems. One is a modification of the Ewald sum; it is known as the "Ewald-Kornfeld summation" technique. Other strategies are the reaction field method and Ladd's multipole expansion method; see [ VESELY 78] and [ ALLEN 90]. 6.5.2 Particle-Mesh Methods (PM and P3M):Huge model systems with $1/r$ potentials (celestial masses or microscopic charged particles) may be described by introducing "superparticles" consisting of some $10^{4}-10^{8}$ ions, electrons, or stars.[ HOCKNEY 81]Neglecting the short-range interactions, Hockney suggested a method to speed up the dynamics due to the far-reaching $1/r$ potential.
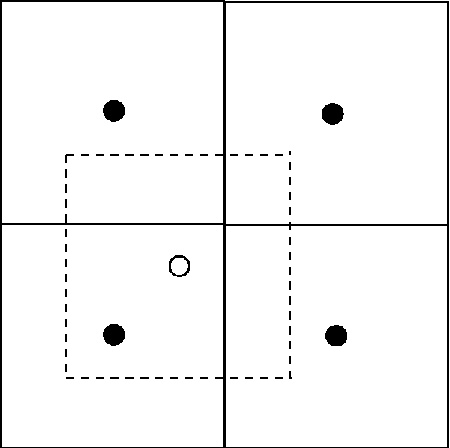
Consider a square cell of $M \times M$
subcells of side length $\Delta x = \Delta y = \Delta l$=.
Each subcell should contain an average of $10-100$ superparticles.
$
\ddot{ r}_{k} = -\frac{\textstyle q_{k}}{\textstyle m_{k}} \nabla_{k}\Phi =
\frac{\textstyle q_{k}}{\textstyle m_{k}} E( r_{k})
$
where $\Phi( r)$ is the electrostatic or gravitational potential. It is determined by the charge (or mass) density $\rho( r,t)$ defined by the positions of all superparticles.
To compute $\Phi( r)$ at time $t_{n}$ at the centers of the
subcells, the given configuration of superions is first replaced by a
lattice-like charge distribution $\rho_{i,j}$. The easiest
discretization method is the nearest grid point (NGP) rule:
$
\rho_{i,j} = \frac{\textstyle 1}{\textstyle (\Delta l)^{2}}
\sum \limits_{k}^{N} q_{k}
\;\delta \left( \frac{\textstyle x_{k}}{\textstyle \Delta l}-i \right)
\delta \left( \frac{\textstyle y_{k}}{\textstyle \Delta l}-j \right)
$
A more refined method of charge assignment than the NGP rule is
the cloud in cell (CIC) prescription:
The next step is the calculation of the potential produced by the charge lattice. Any of the relaxation method of Chapter 5 may be applied, but the FACR technique as developed by Hockney is preferred.[ HOCKNEY 81] Result: values of the potential $\Phi_{i,j}$ at the cell centers. The field strength at the position $r_{k}$ of some superparticle $k$ in cell $(i,j)$ is then
$
\begin{eqnarray}
E_{x}&=&-\left[ \Phi_{i+1,j} - \Phi_{i-1,j} \right]\left/ 2\Delta l \right.
\\
E_{y}&=&-\left[ \Phi_{i,j+1} - \Phi_{i,j-1} \right]\left/ 2\Delta l \right.
\end{eqnarray}
$
Next we integrate the equation of motion:
$
\begin{eqnarray}
r_{k}^{n+1}&=&2 r_{k}^{n}- r_{k}^{n-1}
+\frac{\textstyle q_{k}}{\textstyle m_{k}} (\Delta t)^{2} E_{i,j}^{n} \\
v_{k}^{n}&=&\left[ r_{k}^{n+1}- r_{k}^{n-1}\right] \left/
2\Delta t \right.
\end{eqnarray}
$
which completes the time step. Here is the prescription once more:
Figure 6.10: Particle-mesh method
The PM technique considers only the action of the total field by the distant superparticles. If the short-ranged forces may not be neglected, as in the simulation of molten salts, the Born, Huggins and Mayer potential is included (see Table 6.1):
$
U(r) = \frac{\textstyle q_{i}q_{j}}{\textstyle 4\pi \epsilon_{0}r}+B_{ij}
e^{\textstyle -\alpha_{ij}r} - \frac{\textstyle C_{ij}}{\textstyle r^{6}}
- \frac{\textstyle D_{ij}}{\textstyle r^{8}}
$
Combining the PM method and the molecular dynamics technique [ HOCKNEY 81], we may take into account the short-ranged forces up to a certain interparticle distance, while the long-ranged contributions are included by the particle-mesh procedure. This combination of particle-particle and particle-mesh methods has come to be called PPPM- or P3M technique. vesely 2006
|