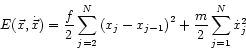This model, introduced by Bunimovich and Sinai, will serve us to demonstrate the existence of chaos even in quite small systems. Chaos, it must be understood, is a fundamental prerequisite for the application of statistical rules. It is a basic property of chaotic systems that they will acquire each one of a certain set of ``states'' with equal probability, i.e. with equal relative frequency. It is this ``equal a priory probability'' of states which we need to proceed into the heart of Statistical Mechanics.
The stadium billiard is defined as follows.
Let a ``light ray'' or ``mass point'' move about in a
two-dimensional container with reflecting or ideally elastic
walls. The boundaries have both flat and semicircular parts, which
gives rise to an efficient mixing of the flight directions upon reflection.
Such a system is chaotic, meaning that the motional degrees of freedom
![]() exhibit a uniform probability distribution.
Since we have
exhibit a uniform probability distribution.
Since we have
![]() the ``phase points'' describing the momentary motion are distributed evenly over the periphery
of a circle. The model is easily extended into three dimensions; the velocity
then has three components, energy conservation keeps the phase points
on the surface of a sphere, and equal a priory probability (or chaos)
means that the distribution of points on this ``energy surface'' is homogeneous - nowhere denser or thinner than elsewhere.
the ``phase points'' describing the momentary motion are distributed evenly over the periphery
of a circle. The model is easily extended into three dimensions; the velocity
then has three components, energy conservation keeps the phase points
on the surface of a sphere, and equal a priory probability (or chaos)
means that the distribution of points on this ``energy surface'' is homogeneous - nowhere denser or thinner than elsewhere.

Applet Stadium: Start |
- See the trajectory of the particle (ray); note the frequency histograms for flight direction
- ``Chaos'' is demonstrated by simultaneously starting a large number of trajectories with nearly identical initial directions:
[Code: Stadium]
 Applet VarSinai:
Start
Applet VarSinai:
Start
|
Simulation: Sinai Billiard
- Ideal one particle gas in a box having randomizers on its walls
- See the trajectory of the particle (ray); note the frequency histograms for flight direction
[Code: VarSinai]
The momentary state of a classical system of ![]() point particles
is completely determined by the specification of
all positions
point particles
is completely determined by the specification of
all positions
![]() and velocities
and velocities
![]() .
The energy contained in the system is entirely kinetic, and in an isolated
system with ideally elastic walls remains constant.
.
The energy contained in the system is entirely kinetic, and in an isolated
system with ideally elastic walls remains constant.
Again,
| (1.19) |
In two dimensions - the box being quadratic with side length ![]() - we
have for the energies
- we
have for the energies
| (1.20) |
If there are ![]() particles in the box we have, in three dimensions,
particles in the box we have, in three dimensions,
Note: In writing the sum 1.21 we only assumed that each
of the ![]() particles is in a certain state
particles is in a certain state
![]()
![]() . We have not considered
yet if any combination of single particle states
. We have not considered
yet if any combination of single particle states
![]() is indeed permitted, or if certain
is indeed permitted, or if certain
![]() might exclude each other (Pauli priciple for
fermions.)
might exclude each other (Pauli priciple for
fermions.)
Again we assume that
At very low densities such a model system will of course resemble a classical ideal gas. However, since there is now a - albeit simplified - mechanism for the transfer of momentum and energy the model is a suitable reference system for kinetic theory which is concerned with the transport of mechanical quantities. The relevant results will be applicable as first approximations also to moderately dense gases and fluids.
In addition, the HS model has a special significance for the
simulation of fluids.

Applet Harddisks: Start |
![$\textstyle \parbox{360pt}{
\mbox{}\\
{\bf Simulation: Hard discs}
\mbox{}\\
-...
...}/v_{x})$ and $x$-speed $v_{x}$.
\\
\vspace{2ex}
{\small [Code: Harddisks]}
}$](img191.png)

Applet Hspheres: Start |
![$\textstyle \parbox{360pt}{
\mbox{}\\
{\bf Simulation: Hard spheres}
\mbox{} ...
...y}/v_{x})$ and $x$-speed $v_{x}$.
\\
\vspace{2ex}
{\small [Code: Hspheres]}
}$](img192.png)
This model fluid is defined by the interaction potential (see figure)
where
In place of the hard collisions we have now a continuous repulsive
interaction at small distances; in addition there is a weak attractive force
at intermediate pair distances. The model is fairly realistic; the interaction
between two rare gas atoms is well approximated by equ. 1.22.
![\begin{figure}\hspace{90pt}
\includegraphics[width=240pt]{fig/f1ljp.ps}\end{figure}](img197.png) |
In simulation one often uses the so-called
``periodic boundary conditions'' instead of reflecting vessel walls:
a particle leaving the (quadratic, cubic, ...) cell on the right is
then fed in with identical velocity from the left boundary, etc.
This guarantees that particle number, energy and total momentum are
conserved, and that each particle is at all times surrounded by
other particles instead of having a wall nearby. The situation of a
molecule well within a macroscopic sample is better approximated
in this way.

Applet LJones: Start |
![$\textstyle \parbox{360pt}{
\mbox{}\\
{\bf Simulation: Lennard-Jones fluid}
\mb...
...x with periodic boundary conditions.
\\
\vspace{2ex}
{\small [Code: LJones]}
}$](img198.png)
The basic model for a solid is a regular configuration of atoms or ions that are bound to their nearest neighbors by a suitably modelled pair potential. Whatever the functional form of this potential, it may be approximated, for small excursions of any one particle from its equilibrium position, by a harmonic potential. Let
where
The generalization of 1.23 to ![]() and
and ![]() dimensions is straightforward.
dimensions is straightforward.
The further treatment of this model is simplified by the approximate
assumption that each particle is moving independently from all others in its
own oscillator potential:
![]()
![]()
![]() .
In going to
.
In going to ![]() and
and ![]() dimensions one introduces the further
simplifying assumption that this private oscillator potential
is isotropically
``smeared out'':
dimensions one introduces the further
simplifying assumption that this private oscillator potential
is isotropically
``smeared out'':
![]()
![]() .
The model thus defined is known as the
``Einstein model'' of solids.
.
The model thus defined is known as the
``Einstein model'' of solids.
Most real substances consist of more complex units than isotropic atoms or Lennard-Jones type particles. There may be several interaction centers per particle, containing electrical charges, dipoles or multipoles, and the units may be joined by rigid or flexible bonds. Some of these models are still amenable to a theoretical treatment, but more often than not the methods of numerical simulation - Monte Carlo or molecular dynamics - must be invoked.
Magnetically or electrically polarizable solids are often described by models in which ``spins'' with the discrete permitted values
If the spins have no mutual interaction the discrete states of such a
system are easy to enumerate. This is why such models are often
used to demonstrate of statistical-mechanical - or actually,
combinatorical - relations (Reif: Berkeley Lectures). The energy
of the system is then defined by
![]() , where
, where ![]() is an external field.
is an external field.
Of more physical significance are those models in which the spins interact with each other, For example, the parallel alignment of two neighboring spins may be energetically favored over the antiparallel configuration (Ising model). Monte Carlo simulation experiments on systems of this type have contributed much to our understanding of the properties of ferromagnetic and -electric substances.
![\begin{figure}\includegraphics[width=240pt]{fig/f1psixy.ps}\end{figure}](img181.png)