| Franz J. Vesely > CompPhys Tutorial > Selected Applications > Evaluation of Simulation Experiments |
6.4 Evaluation of Simulation ExperimentsIn addition to basic thermodynamic observables such as internal energy (eq. 6.1) and pressure (equ. 6.2) many more details about the structure and the dynamics of statistical-mechanical systems may be accessed. Let us consider two such quantities, the pair correlation function $g(r)$ and the velocity autocorrelation function $C(t)$.PROJECT MD/MC (LENNARD-JONES): (See also here) In your Lennard-Jones MD and MC programs, include a procedure to calculate averages of the total potential energy and the virial as defined by
$
W\equiv\sum \limits_{i}\vec{K}_{i}\cdot \vec{r}_{i} = -\frac{\textstyle 1}{\textstyle 2}
\sum \limits_{i} \sum \limits_{j} \vec{K}_{ij}\cdot \vec{r}_{ij}
$
From these compute the internal energy and the pressure. Compare with results from literature, e.g. [ MCDONALD 74, VERLET 67]. Allow for deviations in the $5-10\%$ range, as we have omitted a correction for the finite sample size (`cutoff correction'). Subsections 6.4.1 Pair Correlation FunctionLet
$
a(r;\Gamma_{c}) = \sum \limits_{i}\delta(r_{i}- r)
$
An average of this quantity represents the relative frequency, or probability densitiy of some particle being situated near $r$. In other words, $\langle a(r)\rangle=\rho(r)$ is simply the mean fluid density at position $r$:
$
\rho(r)=\langle \sum \limits_{i}\delta(r_{i}-r)\rangle
$
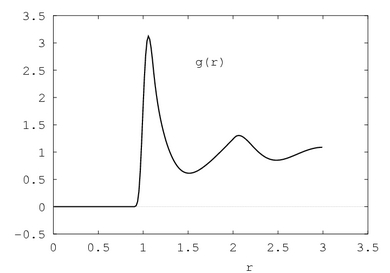
In a fluid we usually have $\rho(r)=const$; only in the presence of external fields or near surfaces $\rho(r)$ varies in a non-trivial manner. Let us proceed to the "pair correlation function" (PCF)
$
g(r)=\frac{\textstyle V}{\textstyle 4\pi r^{2}N^{2}}
\langle\sum \limits_{i} \sum \limits_{j\neq i} \delta (r-r_{ij}) \rangle
$
This is the
conditional probability density of finding a particle at
$r$, given that there is a particle at the coordinate origin.
Thus $g(r)$ provides a measure of local spatial ordering in a fluid.
To determine $g(r)$, proceed like this:
Significance of $g(r)$ in fluid physics:
PROJECT MD/MC (LENNARD-JONES): (See also here) Augment your Lennard-Jones MD (or MC) program by a routine that computes the pair correlation function $g(r)$ according to the procedure given above; remember to apply the nearest image convention when computing the pair distances. As the subroutine ENERGY already contains a loop over all particle pairs $(i,j)$, it is best to increment the $g(r)$ histogram within that loop.
Plot the PCF and see whether it resembles the one given in
Figure 6.6.
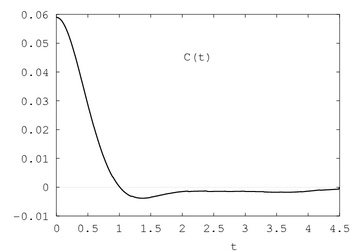
6.4.2 Autocorrelation FunctionsAn elementary example of temporal correlations of the form
$
C_{a}(t) \equiv \langle a(0) a(t) \rangle
$
is the velocity autocorrelation in fluids
$
C(t)\equiv \langle v_{i}(0) \cdot v_{i}(t) \rangle
$
Simple kinetic theory, which takes into account only binary
collisions, predicts $C(t) \propto e^{-\lambda t}$. At fluid densities
a different behavior is to be expected. Nevertheless the first results on
$C(t)$ obtained by Alder [
ALDER 67] provided some surprises.
It turned out that at intermediate fluid densities and long times
$C(t) \propto t^{-3/2}$ instead of showing an exponential decay.
This has profound consequences. The diffusion constant $D$ of a liquid is given by
$
D = \frac{\textstyle 1}{\textstyle 3} \int \limits_{0}^{\infty}C(t) dt
$
Due to the long time tail of $C(t)$ the simulation result for $D$ is about $30$ percent larger than its kinetic estimate.
The reason for the long time tail in $C(t)$ was later explained as a
collective dynamical effect: part of the momentum of a particle
is stored in a microscopic vortex that dies off very slowly.
[DORFMAN 72]
Procedure for calculating autocorrelation functions $ \langle a(0) a(t) \rangle $:
|