| Franz J. Vesely > CompPhys Tutorial > Selected Applications > Molecular Simulation |
6. Simulation and Statistical Mechanics
At time $t$, combine the position vectors of the $N$ atoms into a vector $\Gamma_{c}\equiv$ $\{ r_{1} \dots r_{N}\}$. The set of all possible such vectors spans the $3N$ -dimensional "configuration space" $\Gamma_{c}$. Let $a(\Gamma_{c})$ be a property of the $N$ -body system, depending on the positions of all particles (i.e. of the microstate $\Gamma_{c}$). The thermodynamic average of $a$ is given by
$
\langle a \rangle = \int \limits_{\textstyle \Gamma_{\textstyle c}} a(\Gamma_{c})
p(\Gamma_{c}) d\Gamma_{c}$
where $p(\Gamma_{c})$ is the probability density at the configuration space point $\Gamma_{c}$. Examples:
Problem: the probability density $p(\Gamma_{c})$ is known only up to an indetermined normalizing factor. Thus, $p_{can}(\Gamma_{c})$ $\propto exp[-E(\Gamma_{c})/kT]$ but the normalizing denominator $Q$ (the Configurational Partition Function) in
$
1 = \int p(\Gamma_{c}) d\Gamma_{c} \equiv \frac{\textstyle 1}{\textstyle Q}
\int e^{\textstyle -E(\Gamma_{c})/kT} d\Gamma_{c}
$
is not known. Spin systems: Basic model of ferromagnetic solids: atoms are fixed on the vertices of a lattice. Their dipole vectors (spins) may have varying directions: either up/down (Ising model) or any direction (Heisenberg model). Microscopic configuration $\Gamma_{c}$: given by the $N$ spins on the lattice. Example: Two-dimensional square Ising lattice; only the four nearest spins contribute to the energy of spin $\sigma_{i}$ ($= \pm 1$). (Three dimensions: six nearest neighbors). The total energy is
$
E=-\frac{A}{2}\sum \limits_{i}^{N} \sum \limits_{j(i)}^{4\; or \;6} \sigma_{i}
\sigma_{j(i)}
$
($A$ ... coupling constant). $\Longrightarrow$ Magnetic polarization
$M \equiv \sum \limits_{i}^{N} \sigma_{i}$
may be determined as a function of temperature. If a magnetic field $H$ is applied, the additional potential energy is $E_{H}=-H \sum \limits_{i} \sigma_{i}$. 6.1.2 Technical Matters
Units: To avoid the handling of small numbers, choose units appropriate to the model. Lennard-Jones: Energy unit $E_{0}=\epsilon$; length $l_{0}=\sigma$. The pair energy is then
$u_{LJ}^{*} = 4 \, \left[ r^{*-12}-r^{*-6} \right]$
where $u^{*} \equiv u/\epsilon$ and $r^{*} \equiv r/\sigma$. As the third mechanical unit, choose the atomic mass $m_{0}=1AMU= 1.6606 \cdot 10^{-27}kg$. The time unit is now the combination $t_{0}=\sqrt{m_{0} \sigma^{2}/\epsilon}$. Electrical charge: best measured in multiples of the electron charge, $q_{0}= 1.602 \cdot 10^{-19} As$. Number density: $\rho=N/V$ is a large number; therefore we reduce it by a suitable standard density, $\rho_{0}/\sigma^{3}$: $\rho^{*} \equiv N \sigma^{3}/V$. Temperature: $T_{0}=\epsilon/k$ Hard spheres: no "natural" unit of energy; therefore choose self-consistent time unit $t_{0}=\sqrt{m_{0}d^{2}/kT}$. For hard spheres of diameter $d_{0} =2 r_{0}$ the customary standard density is $\rho_{0}=\sqrt{2}/d_{0}^{3}$; thus: $\rho^{*}=N d_{0}^{3}/V\sqrt{2}$. Periodic boundary conditions (PBC) and nearest image convention (NIC): To avoid "wall effects" we surround the basic cell containing the $N$ particles by periodic images of itself. Spin lattices: In each coordinate direction the last ("rightmost") spin in a row interacts also with a right neighbor, which is taken to be identical to the first (leftmost) spin in that row, and vice versa (see Figure). 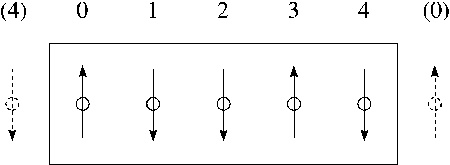 Figure:
Periodic boundary conditions on a spin lattice
Figure:
Periodic boundary conditions on a spin lattice
Fluid: Apply the following rule: For each particle $i$ store, instead of any coordinate $x_{i}$, the quantity
$(x_{i}+2L) \mbox{mod} L $
(with $L$ the side length of the cell). When a particle leaves the cell to the right, it is automatically replaced by a particle entering from the left, etc. Nearest Image Convention: In computing pair vectors between two particles $i$ and $j$ one needs only differences of coordinate values. If this coordinate difference $\Delta x_{ij} \equiv x_{j}-x_{i}$ is larger than $L/2$, then the particle $j$ will not be regarded as an interaction partner of $i$; instead, its left periodic image with coordinate $x_{j}-L$ interacts with $i$. The NIC rule may be implemented by a sequence of IF commands or by the more compact code line
$
\Delta x = \Delta x - L \cdot \mbox{nint}\left( \frac{\textstyle \Delta x}{\textstyle L}\right)
$
where nint($a$) denotes the rounded value of $a$, i.e. the integer nearest to $a$. This formulation of NIC is also better suited for vectorising compilers. Starting configuration: On an Ising lattice, draw $N$ spin values with equal probabilities for $+ 1$ and $-1$. Molecules in disordered media: Overlaps must be avoided. $\Longrightarrow$ Place the molecules on a lattice, then "melt" this crystal before the actual simulation run: Thermalization. Population number in a cubic cell with face-centered cubic arrangement: $4m^{3}$, with $m=1,,2,\dots$. Therefore typical particle numbers in simulations are $N = 32, 108, 256, 500$ etc. Adjusting density and temperature: Given $N$, the density is adjusted to a desired value by shrinking or expanding the volume: scale all coordinates by a suitable factor. The temperature is a constant parameter in an MC simulation. In molecular dynamics it must be adjusted in the following manner. Since
$
T=m \langle| v|^{2} \rangle/3k
$
(with $k=1.3804 \cdot 10^{-23} J/deg$) or, in reduced units,
$
T^{*}=m^{*} \langle | v^{*}|^{2} \rangle/3
$
we first take the average of $| v^{*}|^{2}$ over a number of MD steps to determine the actual temperature of the simulated system. Then we scale each velocity component according to
$
v_{i,x} \leftrightarrow v_{i,x} \sqrt{T^{*}_{desired}/T^{*}_{actual}}
$
Since $T^{*}$ is a fluctuating quantity it can be adjusted only approximately. EXERCISE: (See also here) Reduced units: Consider a pair of Lennard-Jones particles with $\epsilon=1.6537\cdot 10^{-21} J$ and $\sigma=3.405 \cdot 10^{-10} m$ (typical for Argon). Let the two molecules be situated at a distance of $3.2 \cdot10^{-10}m$ from each other. - Calculate the potential energy of this arrangement. - Do the same calculation using $\epsilon$ and $\sigma$ as units of energy and length, respectively. These parameters then vanish from the expression for the pair energy, and the calculation is done with quantities of order $1$. - With the above units for energy and length, together with the atomic mass unit, compute the metric value of the self-consistent unit of time? Let one of the particles have a metric speed $v=500 m/s$, typical of the thermal velocities of atoms or small molecules. What is the value of $v$ in self-consistent units? PROJECT MC/MD: (See also here) As a first reusable module for a simulation program, write a code to set up a cubic box of side length $L$ inhabited by up to $N =4 m^{3}$ particles in a face-centered cubic arrangement. Use your favourite programming language and make the code flexible enough to allow for easy change of volume (i.e. density). Make sure that the lengths are measured in units of $\sigma_{LJ}$. For later reference, let us call this subroutine STARTCONF. Advice: It is convenient to count the lower, left and front face of the cube as belonging to the basic cell, while the three other faces belong to the next periodic cells.
To test for correct arragement of the particles, compute the diagnostic
$S_{0} \equiv \frac{1}{3} \sum \limits_{i}^{N} \left[
\cos (4 m \pi x_{i}/L)+\cos (4 m \pi y_{i}/L)+
\cos (4 m \pi z_{i}/L) \right]
$
which is sometimes called "melting factor". For a fcc configuration it should be equal to $N$ (why?). By scaling all lengths, adjust the volume such that the reduced number density becomes $\rho^{*}=0.6$.
Augment the subroutine STARTCONF by a procedure that assigns random
velocities to the particles, making sure that the
sum total of each velocity component is zero.
$
E_{pot}=\frac{1}{2}\sum \limits_{i} \sum \limits_{j \neq i} u_{LJ}(r_{ij})
= \sum \limits_{i}^{N-1} \sum \limits_{j=i+1}^{N} u_{LJ}(r_{ij})
$
Write such a subroutine and call it ENERGY. Use it to compute the energy in the system created by STARTCONF. vesely 2006
|
