


Next: 1.4 Sample Applications
Up: 1.3 Difference Quotients
Previous: 1.3.3 First derivatives in
1.3.4 Second derivatives in 2 dimensions
By again fixing one of the independent variables
-  , say - and considering only
, say - and considering only  , we obtain, in terms of the
Stirling (centered) approximation,
, we obtain, in terms of the
Stirling (centered) approximation,
Analogous (and less accurate) formulae are valid within the
NGF- and NGB-approximations, respectively.
How about
mixed derivatives?
Mixed derivatives
Approximating  use the same
kind of approximation with respect to both the
use the same
kind of approximation with respect to both the  - and the
- and the  -direction.
(This may not hold if
-direction.
(This may not hold if  and
and  have a different character, e.g. one
space and one time variable.)
have a different character, e.g. one
space and one time variable.)
Stirling:
And now, fow for the
curvature of  :
:
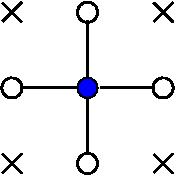
Curvature of a function f(x,y)
To find the local curvature at the grid point
 we have to apply the nabla operator
we have to apply the nabla operator  twice.(*)
There are two ways:
twice.(*)
There are two ways:
Either ``difference'' along the grid axes,
or apply ``diagonal differencing'', writing
| |

|
| | ||
Axial vs. diagonal differencing
|
(*) Note that the nabla operator  mentioned here is not
to be mixed up with the backward difference for which we
use the same symbol.
mentioned here is not
to be mixed up with the backward difference for which we
use the same symbol.



Next: 1.4 Sample Applications
Up: 1.3 Difference Quotients
Previous: 1.3.3 First derivatives in
Franz J. Vesely Oct 2005
See also: "Computational Physics - An Introduction," Kluwer-Plenum 2001
![$\displaystyle \frac{1}{(\Delta x)^{2}} [f_{i+1,j}-2f_{i,j}+f_{i-1,j}]
+O[(\Delta x)^{2}]$](img126.png)
![$\displaystyle \frac{\delta_{i}^{2}f_{i,j}}{(\Delta x)^{2}}
+ O[(\Delta x)^{2}]$](img127.png)
![$\displaystyle \frac{1}{(\Delta x)^{2}} [f_{i+1,j}-2f_{i,j}+f_{i-1,j}]
+O[(\Delta x)^{2}]$](img126.png)
![$\displaystyle \frac{\delta_{i}^{2}f_{i,j}}{(\Delta x)^{2}}
+ O[(\Delta x)^{2}]$](img127.png)
![]() use the same
kind of approximation with respect to both the
use the same
kind of approximation with respect to both the ![]() - and the
- and the ![]() -direction.
(This may not hold if
-direction.
(This may not hold if ![]() and
and ![]() have a different character, e.g. one
space and one time variable.)
have a different character, e.g. one
space and one time variable.)
![$\displaystyle \frac{1}{4\Delta x \Delta y} \left[ f_{i+1,j+1}-f_{i+1,j-1}-
f_{i-1,j+1}+f_{i-1,j-1} \right] +O[\Delta x \Delta y]$](img130.png)
![$\displaystyle \frac{\mu \delta_{i}}{\Delta x}
\left[\frac{\mu \delta_{j} f_{i,j}} {\Delta y} \right]
+O[\Delta x \Delta y]$](img131.png)
![]() :
: ![]() we have to apply the nabla operator
we have to apply the nabla operator ![]() twice.(*)
There are two ways:
twice.(*)
There are two ways:
![$\displaystyle \frac{1}{(\Delta l)^{2}}
\left[ f_{i+1,j}+f_{i,j+1}+f_{i-1,j}+f_{i,j-1}-4f_{i,j}\right]$](img135.png)
![$\displaystyle \frac{1}{2(\Delta l)^{2}}
\left[ f_{i+1,j+1}+f_{i-1,j+1}+f_{i-1,j-1}+f_{i+1,j-1}-4f_{i,j}\right]$](img137.png)

