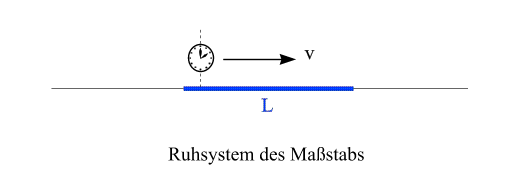
Betrachten wir folgende Situation: Gegeben sei ein Maßstab, der in einem Inertialsystem ruht und die Länge L hat. Entlang dieses Maßstabs bewege sich eine Uhr mit Geschwindigkeit v nach rechts. Das ist in der folgenden Abbildung dargestellt:

Wie lange braucht die Uhr, um sich am Maßstab vorbeizubewegen? Sie kommt zunächst von links, bewegt sich auf ihn zu, erreicht sein linkes Ende (diese Begegnung nennen wir das Ereignis G), bewegt sich entlang des Maßstabs, erreicht schließlich sein rechtes Ende (das nennen wir das Ereignis H) und verlässt die Szene, indem sie sich nach rechts entfernt. Die Frage lautet dann: Wieviel Zeit vergeht zwischen den Ereignissen G und H? Nun wollen wir ein bisschen vorsichtig sein und unterscheiden:

• Im Ruhsystem des Maßstabs vergeht zwischen den beiden Ereignissen G und H ein bestimmtes Zeitintervall.
• Die Uhr selbst misst zwischen den Ereignissen G und H ein bestimmtes Zeitintervalll.

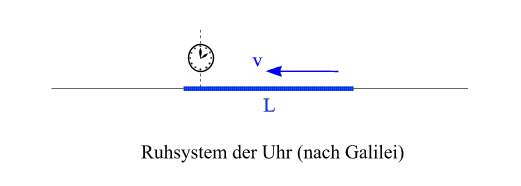
Wir wissen bereits, dass diese beiden Zeitintervalle nicht gleich groß sind: das ist der Effekt der Zeitdilatation. Im Ruhsystem des Maßstabs gemessen, geht die Uhr langsamer als in ihrem eigenen Ruhsystem. Das im Ruhsystem des Maßstabs gemessene Zeitintervall zwischen den Ereignissen G und H ist daher länger als die Zeit, die zwischen diesen beiden Ereignissen für die Uhr selbst vergangen ist. Das im Ruhsystem des Maßstabs gemessene Zeitintervall ist gerade jene Zeit, die man benötigt, um eine Strecke der Länge L mit Geschwindigkeit v zurückzulegen (also L/v). Wir halten fest: Die Zeitspanne, die für die Uhr selbst vergangen ist, ist kleiner als L/v.

Nun betrachten wir dieselbe Situation, wie sie sich im Ruhsystem der Uhr darstellt: Nach der galileischen Physik wäre folgendes zu erwarten:

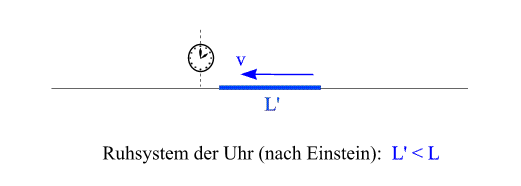
Im Ruhsystem der Uhr bewegt sich der Maßstab mit Geschwindigkeit v nach links. Die Länge des Stabes ist nach wie vor L (denn in der galileischen Physik ist die Länge eines Körpers unabhängig vom Inertialsystem, in dem sie gemessen wird). Jetzt kann aber etwas nicht stimmen: Da die Uhr an einem Maßstab der Länge L mit Geschwindigkeit v vorbeifliegt, sollte für sie (in ihrem Ruhsystem) der Prozess des Vorbewegens gerade so lange dauern, wie man benötigt, um eine Strecke der Länge L mit Geschwindigkeit v zurückzulegen (d.h. L/v). Andererseits haben wir aber soeben aufgrund des Effekts der Zeitdilatation festgestellt, dass die für die Uhr in ihrem Ruhsystem vergangene Zeit kleiner als L/v ist. Wenn die Uhr zum Vorbeibewegen also weniger Zeit zur Verfügung hat, stellt die obige Abbildung die Situation nicht korrekt dar und muss durch folgende ersetzt werden:

Die Länge des Maßstabs ist - wenn sie im Ruhsystem der Uhr gemessen wird - kleiner als L, damit der Maßstab es schafft, sich an der Uhr in der zur Verfügung stehenden (kürzeren) Zeit an ihr vorbeizubewegen! Konkret ist er um denselben Faktor "geschrumpft", um den die Uhr im Ruhsystem des Maßstabs langsamer geht als in ihrem eigenen Ruhsystem.

Das Postulat von der Konstanz der Lichtgeschwindigkeit zieht also neben dem Effekt der Zeitdilatation eine weitere Konsequenz nach sich. Kurz ausgedrückt lautet sie

"Bewegte Maßstäbe sind in Bewegungsrichtung verkürzt."

Dieser Effekt heisst Lorentzkontraktion (oder Längenkontraktion).

Wir wollen hinzufügen, dass es keinen derartigen Effekt quer zur Bewegungsrichtung gibt. (Die im Abschnitt über die Zeitdilatation behandelte Lichtuhr ist ein Beispiel dafür: der Abstand zwischen den Spiegeln ist in beiden Inertialsystemen der gleiche). Wenn man also einen Körper, der in seinem Ruhsystem eine Kugel ist, in einem dagegen bewegten Inertialsystem vermisst, so müsste man feststellen, dass es sich nun um ein Ellipsoid handelt, dessen in Bewegungsrichtung liegende Achse verkürzt ist, während die beiden anderen Achsen mit dem im Ruhsystem gemessenen Kugelradius übereinstimmen.
 

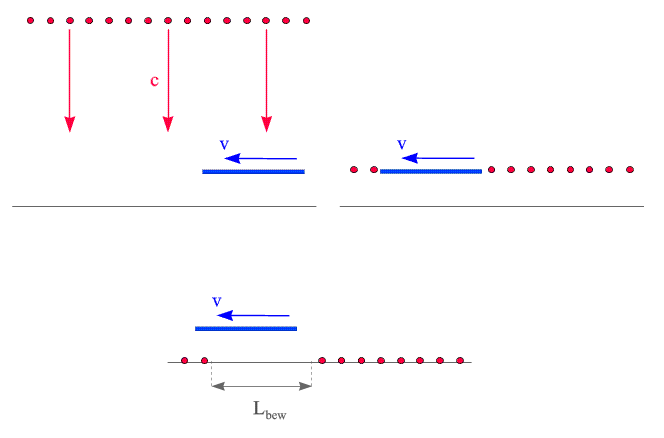
Um die oben dargestellte Argumentation quantitativ zu analysieren, ist fast kein Aufwand mehr nötig. Wir bezeichnen die Länge des Maßstabs im Ruhsystem der Uhr (d.h. in dem System, in dem er sich bewegt), mit L_bew . Weiters geben wir den Zeiten, die das Vorbeifliegen in beiden Systemen dauert, Namen:

• Im Ruhsystem des Maßstabs vergeht zwischen den Ereignissen G und H das Zeitintervall Dt = L/v.
• Die Uhr selbst misst zwischen den Ereignissen G und H das (kleinere) Zeitintervall Dt (1 - v²/c² )^1/2.

Im Ruhsystem der Uhr hat der Maßstab also die Länge L_bew und benötigt fürs Vorbeifliegen die Zeit Dt (1 - v²/c² )^1/2. Folglich gilt

wobei wir v Dt = L verwendet haben. Unser Resultat lautet also

wobei wir nun die Größe L (die Länge des Maßstabs in seinem Ruhsystem) in L_Ruh umbenannt haben. Das ist die Formel für die Lorentzkontraktion, die wir kompakter auch als  L_bew  =  L_Ruh (1 - v²/c² )^1/2  schreiben können. In Worten kann dieser Effekt so formuliert werden:

Ebenso wie bei der Zeitdilatation handelt es sich dabei nicht um eine Art "scheinbaren Effekt" oder eine "Täuschung" - es ist hier die tatsächliche Länge, wie sie in einem relativ zum Objekt bewegten Inertialsystem gemessen wird, gemeint. Räumliche Abstände sind - ebenso wie Zeitintervalle - keine universellen Größen, sondern hängen vom Bewegungszustand des Beobachters ab. In diesem Sinn hat auch der "Raum" den absoluten Charakter - den er in der galileischen Physik hatte - verloren.
 

Die Logik dieses Effekts enthält einige Fallstricke, die sein Verständnis erschweren. Eine dieser Schwierigkeiten betrifft den Begriff der Länge eines bewegten Objekts. Wie können wir sie messen? Um es anhand eines Gedankenexperiments ganz konkret zu machen: Wie messen wir die Länge einer Schildkröte (in Bewegungsrichtung), die gerade "geradlinig gleichförmig" durchs Zimmer kriecht, und zwar im Bezugssystem des Zimmers (das wir auf eine einzige räumliche Dimension beschränken und als Inertialsystem ansehen wollen)?

Die sich aufdrängende Antwort "Indem wir einen Maßstab mit ihr mitbewegen und ablesen" ist falsch: Wenn sich der Maßstab mit der Schildkröte mitbewegt, messen wir auf diese Weise ihre Länge in ihrem eigenen Ruhsystem (die Größe L_Ruh ), nicht aber ihre Länge im System des Zimmers, d.h. die Größe, die wir vorhin mit L_bew bezeichnet haben! In der galileischen Physik - und auch in unserem Alltagsleben - stellt sich diese Unterscheidung gar nicht, da angenommen wird, dass beide Größen übereinstimmen.

Wir besprechen zwei Möglichkeiten, die Länge der Schildkröte im Bezugssystem des Zimmers zu messen. Die erste besteht darin,

Die Länge der Schildkröte im Inertialsystem des Zimmers ist dann das Produkt aus der in Punkt 1 gemessenen Zeit und der in Punkt 2 gemessenen Schildkrötengeschwindigkeit. Die Größe "Länge" wird hier also auf das Produkt "Zeit mal Geschwindigkeit" zurückgeführt. Das ist zulässig, da die Geschwindigkeit ja als Quotient aus Weg ( = zurückgelegte "Länge") und benötigter Zeit definiert ist. In der oben vorgeführten Argumentation zur Herleitung der Lorentzkontraktion ist genau eine solche "Längenmessung" vorgenommen worden.

Für eine zweite, direktere Methode, die Länge der Schildkröte im Inertialsystem des Zimmers zu messen, ist es notwendig, zwei Ereignisse zu bestimmen, eines am Hinterende (wir nennen es C) und eines am Vorderende der Schildkröte (dieses nennen wir D), die im System des Zimmers gleichzeitig stattfinden. Die Länge der Schildkröte im System des Zimmers ist dann der räumliche Abstand zwischen diesen beiden Ereignissen. Um zwei derartige Ereignisse zu erzeugen, stehen wiederum mehrere Verfahren zur Verfügung:

Es lässt sich zeigen (obwohl wir das hier nicht im Einzelnen vorführen), dass all diese Verfahren zur Längenbestimmung eines bewegten Körpers dasselbe Resultat liefern. Die auf der zweiten Methode beruhenden Verfahren (in denen zwei im Zimmer gleichzeitige Ereignisse C und D die Schlüsselrolle spielen) sind ein bisschen allgemeiner, da die erste Methode nur im Fall von Objekten funktioniert, die sich geradlinig gleichförmig bewegen, und deren Länge sich im Laufe der Bewegung nicht ändert. Die zweite hingegen ist eine ganz allgemeine Definition dessen, was wir unter der "momentanen" Länge eines Objekts in einem gegebenen Inertialsystem verstehen.
 

Als letzte Anstrengung, um den Effekt der Lorentzkontraktion besser zu verstehen, werden wir ihn nun mit der Zeitdilatation vergleichen. Hier liegt ein weiterer Fallstrick auf der Lauer. Bisweilen begegnet man folgender - allzu salopper - Argumentation:

1. In der Speziellen Relativitätstheorie spielen Raum und Zeit in vieler Hinsicht eine ganz ähnliche Rolle (wer zur Lorentztransformation vorblättert, kann diese Ähnlichkeit anhand der dortigen Formeln (9) bestaunen - sie wird noch eindrucksvoller, wenn c = 1 gesetzt wird).
2. Zeitintervalle und Längen hängen vom Bewegungszustand des Beobachters ab. Dabei handelt es sich um ganz analoge Effekte: Bewegte Uhren gehen langsamer, und bewegte Maßstäbe sind verkürzt.
3. Dass bewegte Uhren langsamer gehen, wird durch die Formel  Dt_bew  =  Dt_Ruh (1 - v²/c² )^-1/2  ausgedrückt.
4. Durch Analogie schließen wir, dass für Längen die Formel  L_bew  =  L_Ruh (1 - v²/c² )^-1/2  gilt.

Leider ist die letzte Formel falsch (sie sagt ja aus "bewegte Maßstäbe sind verlängert"), wie der Vergleich mit (2) zeigt. (Wir wollen in Klammer anmerken, dass manchmal auch eine auf die Form der Lorentztransformation gegründete Argumentationsweise zu sehen ist, die zu dem gleichen - falschen - Schluss kommt).

Der Fehler liegt nicht darin, dass Raum und Zeit nicht ähnliche Rollen spielen würden (das tun sie tatsächlich weitgehend!), sondern darin, dass die beiden physikalischen Situationen "Bewegung einer Uhr" und "Bewegung eines Maßstabs" gänzlich voneinander verschieden sind:

• Eine Uhr ist ein lokalisiertes Objekt. Ihre räumliche Ausdehnung ist für den Effekt der Zeitdilatation unbedeutend. Ihre Bewegung wird durch eine einzige Weltlinie charakterisiert.
• Ein Maßstab ist ein ausgedehntes Objekt. Der Effekt der Lorentzkontraktion hat seine räumliche Ausdehnung (Länge) zum Gegenstand. Da der Maßstab aus (unendlich) vielen Punkten besteht, beinhaltet er genau genommen (unendlich) viele Weltlinien. Zum Glück benötigen wir nur zwei Weltlinien, um seine Bewegung zu charakterisieren: die seines linken und die seines rechten Endes. Jedes Ereignis zwischen diesen beiden Weltlinien findet irgendwann irgendwo auf dem Maßstab statt. (Wir sprechen auch von der "Weltfläche" des Maßstabs).

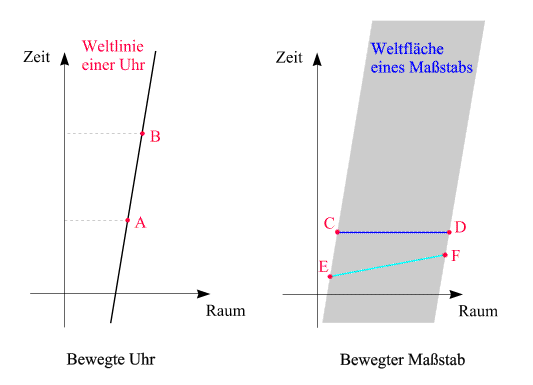
Dieser Unterschied kommt in den folgenden Raumzeit-Diagrammen zum Ausdruck:

Während

• der Effekt der Zeitdilatation Auskunft über die zwischen zwei Ereignissen (A ..."tick" und B ..."tack") stattfindende Zeit gibt (wie sie im gegebenen Inertialsystem gemessen wird),
• sagt der Effekt der Lorentzkontraktion etwas über die Länge der dunkelblau eingezeichneten Strecke aus. Sie ist dadurch charakterisiert, dass alle Ereignisse auf ihr im gegebenen Inertialsystem gleichzeitig sind. Das gilt insbesondere für die Ereignisse C und D (das sind genau jene, die im obigen Schildkrötenbeispiel unter denselben Namen aufgetreten sind). Im Fall der Zeitdilatation existiert eine derartige Gleichzeitigkeitsbedingung nicht, da die Uhr als lokalisiertes Objekt angesehen wird.

Dieser Unterschied bewirkt, dass die Formeln für die beiden Effekte nicht zueinander symmetrisch sind. Für jene, die sich jetzt fragen, wo die Länge des Maßstabs, wie sie in seinem Ruhsystem gemessen wird, hier vorkommt, wiederholen wir das vorige Diagramm, allerdings mit einer zusätzlich eingezeichneten Linie:

Alle Ereignisse, die auf der hellblauen Strecke liegen (insbesondere E und F), finden im Ruhsystem des Maßstabs gleichzeitig statt! Sie repräsentiert die Lage des Maßstabs zu einer bestimmten Zeit in seinem Ruhsystem. Sie stellt ein "jetzt" im Ruhsystem des Maßstabs dar, und daher ist sie (und nicht die dunkelblaue Strecke) für die Längenmessung in diesem System relevant. (Wir werden wir im Abschnitt über die Lorentztransformation genauer besprechen, wie Ereignisse, die in einem Inertialsystem gleichzeitig sind, in einem anderen Inertialsystem beobachtet werden. Am Ende des betreffenden Abschnitts wird auch die Aufklärung, warum die hellblaue Strecke unter einem solch eigenartigen Winkel zu sehen ist, nachgetragen. Wer jetzt nicht vorblättern will, wird gebeten, die Lage dieser Strecke und der Ereignisse E und F einfach zu glauben).
Achtung: Die Länge des Maßstabs im Ruhsystem ist nicht mit der Länge dieser Strecke im Diagramm identisch! (Dieses "Einheiten-Problem" existiert auch im Fall der Zeitdilatation: Die Zeit, die zwischen den Ereignissen A und B im Ruhsystem der Uhr vergeht, kann nicht als Länge der Strecke AB im linken Diagramm abgelesen werden. Diese Feinheit der Raumzeit-Diagramme wird sich in den abschließenden Bemerkungen des Abschnitts über die Geometrie der Raumzeit ganz zwanglos aufklären).
Die Gegenüberstellung der beiden Diagramme illustriert jedenfalls sehr schön, um wieviel einfacher die Logik der Zeitdilatation ist als jene der Lorentzkontraktion.

Aufgabe hierzu:

• Zeichnen Sie ein Raumzeit-Diagramm dieser Art, in dem die in der obigen Herleitung der Lorentzkontraktion auftretenden Ereignisse G und H dargestellt sind!