Wir haben in den vorangegangenen Abschnitten erfahren, dass Zeitintervalle und räumliche Distanzen beobachterabhängig sind. Die Effekte der Zeitdilatation und der Lorentzkontraktion ziehen eine Reihe von Konsequenzen nach sind. Unter anderem ist der Begriff der Geschwindigkeit davon betroffen. In einem gegebenen Inertialsystem ist die Geschwindigkeit - wie üblich - als Quotient aus zurückgelegtem Weg und dafür benötigte Zeit definiert. Wie verhalten sich aber die Werte der Geschwindigkeit eines Objekts, die in verschiedenen Inertialsystemen gemessen werden, zueinander?

Stellen etwa wir uns vor,

• ein Zug fährt (relativ zu den Schienen) mit einer Geschwindigkeit von 60 km/h, und
• innerhalb des Zuges rollt eine Bowlingkugel mit 5 km/h (relativ zum Zug) in Fahrtrichtung.

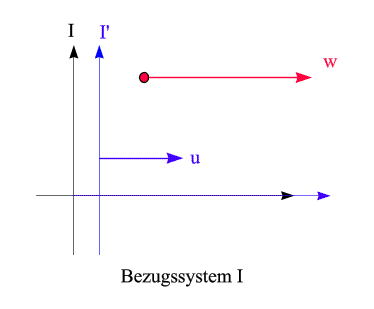
Wie groß ist die Geschwindigkeit der Bowlingkugel im Inertialsystem der Schienen? Nach der galileischen Physik wäre das gerade die Summe der beiden Einzelgeschwindigkeiten, also 65 km/h. Gilt diese Methode, Geschwindigkeiten zu addieren, auch in der Relativitätstheorie?

Eigentlich müssen wir von vornherein erwarten, dass das nicht der Fall ist: Wenn sich etwa der Zug (relativ zu den Schienen) mit 3/4 der Lichtgeschwindigkeit bewegt und die Bowlingkugel (relativ zum Zug) ebenfalls mit 3/4 der Lichtgeschwindigkeit, so würde diese Methode auf die eineinhalbfache Lichtgeschwindigkeit für die Kugel im System der Schienen führen! Das wäre ein hübscher Widerspruch zur Aussage, dass sich kein materieller Körper schneller als das Licht bewegen kann (die im Abschnitt über die Zeitdilatation begründet worden ist).

Tatsächlich gilt die Regel von der simplen Addition der Zahlenwerte der Geschwindigkeiten in der Speziellen Relativitätstheorie nicht.

Um die Lage abzuklären, betrachten wir folgende Situation: Wir benötigen zwei Inertialsysteme - wir nennen sie I (Schienen) und I' (Zug) - und ein gleichförmig bewegtes Objekt (Bowlingkugel). Dabei sollen alle auftretenden Bewegungen nur in einer Raumdimension stattfinden. Das System I' (genauer: sein Ursprung) bewegt sich im System I mit Geschwindigkeit u. Die Kugel bewegt sich in I' mit Geschwindigkeit v und in I mit Geschwindigkeit w. Die folgende Abbildung (sie zeigt die räumlichen Koordinatensysteme, die Bewegung findet in horizontaler Richtung statt) illustriert, wie sich die Situation im System I darstellt:

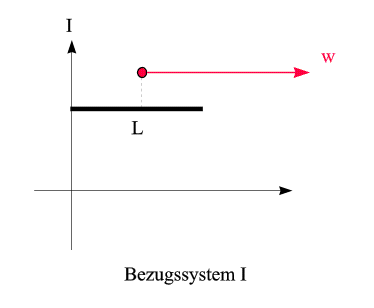
Nach der galileischen Physik wäre zu erwarten, dass w = u + v gilt. Wir werden die Situation nun quantitativ analysieren und eine relativistisch korrekte Formel herleiten, die diese Aussage (die, wie wir gerade gesehen haben, so nicht stimmen kann) ersetzt. Wir stellen uns vor, dass u und v gegeben sind, und wir wollen w berechnen.

Dazu betrachten wir einen Maßstab, der im System I in Ruhe ist und dort die Länge L hat:

Die Kugel bewegt sich in Längsrichtung am Maßstab vorbei. Dabei wollen wir zwei Ereignissen einen Namen geben: A (die Kugel passiert das linke Ende des Maßstabs) und B (die Kugel passiert das rechte Ende des Maßstabs). Die Zeit, die - im System I - zwischen diesen beiden Ereignissen vergeht, d.h. die Zeit, die das Vorbeibewegen dauert, sei mit Dt bezeichnet. Daher gilt die Beziehung

Aufgrund des Effekts der Zeitdilatation (dortige Formel (2)) vergeht im Ruhsystem der Kugel zwischen den Ereignissen A und B die (kürzere) Zeit

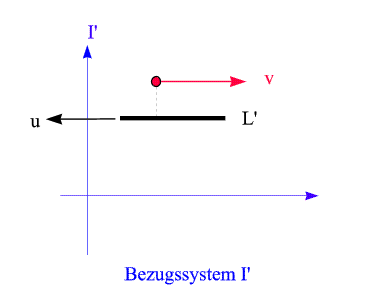
Nun sehen wir uns an, wie derselbe Prozess im Inertialsystem I' aussieht:

Die Kugel bewegt sich mit der Geschwindigkeit v nach rechts, der Maßstab mit der Geschwindigkeit u nach links. Letzterer ist nun aufgrund des Effekts der Lorentzkontraktion (dortige Formel (2)) kürzer als in seinem Ruhsystem I, seine Länge in I' ist

Wir benötigen nun die Zeit Dt', die während des Vorbeibewegens der Kugel am Maßstab (d.h. zwischen den beiden Ereignissen A und B) im System I' vergeht. Das führt auf eine einfache Fahrplanaufgabe: Wenn die Kugel und das linke Ende des Maßstabs beide ihre Bewegung am Ort x' = 0 beginnen, ist die Kugel nach der Zeit Dt' am Ort v Dt' und das rechte Ende des Maßstabs am Ort L' - u Dt'. Die Zeit, zu der die Kugel auf das rechten Ende des Maßstabs trifft, erfüllt daher die Gleichung v Dt' = L' - u Dt'. Wir lösen auf und erhalten

Aufgrund der Zeitdilatation (dortige Formel (2)) ist der Zusammenhang zwischen dieser Größe und der im Ruhsystem der Kugel für denselben Prozess vergangenen Zeit Dt_o durch

gegeben. In den Beziehungen (1) bis (5) steckt nun genügend Information, um w durch u und v auszudrücken: Aufgrund von (1) ist w = L/Dt. Wir benützen (2), um Dt durch Dt_o und w auszudrücken, ersetzen dann mit Hilfe von (3) L durch L' und u und mit Hilfe von (5) Dt_o durch Dt' und v. Schließlich ersetzen wir Dt' mittels (4), wodurch sich ein L' im Zähler gegen ein L' im Nenner wegkürzt. Alle Größen ausser den drei Geschwindigkeiten sind verschwunden, und wir erhalten

Diese Beziehung wird quadriert und ein bisschen umgeformt, sodass die Beziehung

entsteht. Nun ziehen wir die Wurzel und sind am Ziel: Die gesuchte Geschwindigkeit w ist durch

gegeben. Das ist die Formel für die relativistische Geschwindigkeitsaddition. Entgegen ihrer etwas unglücklichen Bezeichnung handelt es sich nicht um eine simple Addtition von Zahlen, und wir sollten das Wort "Addition" hier nur unter Anführungszeichen verstehen.

Das Resultat (8) gilt unabhängig von den Vorzeichen der beteiligten Geschwindigkeiten: u und/oder v dürfen durchaus auch negativ sein (was Bewegungen nach links entspricht). Die einzige Bedingung für ihre Gültigkeit ist, dass die auftretenden Relativbewegungen (Inertialsysteme und Kugel) nur in einer einzigen Raumdimension stattfinden, und dass die Beträge der Geschwindigkeiten kleiner c sind. (Die Geschwindigkeit der Kugel darf im Grenzfall gleich c sein). Kommen zwei Richtungen vor, und sind u und v (nicht parallele) Vektoren, dann muss (8) durch eine allgemeinere Form ersetzt werden, auf die wir hier aber nicht weiter eingehen. (Literaturtipp hierzu: R. Sexl und H. K. Urbantke: Relativität, Gruppen, Teilchen, Springer-Verlag).
 

Falls die Geschwindigkeiten u und v klein gegenüber der Lichtgeschwindigkeit c sind (wie etwa im Fall des eingangs erwähnten Beispiels mit dem Zug und der Bowlingkugel), ist der Nenner in (8) sehr nahe bei 1, und die Geschwindigkeit w ist näherungsweise durch die Summe u + v gegeben, wie es dem Resultat der galileischen Physik entspricht. Setzen wir beispielsweise die Werte des zu Beginn dieses Abschnitts gegebenen Beispiels u = 60 km/h und v = 5 km/h ein, so berechnen wir w = 64.99999999999999 km/h.

Sind große Geschwindigkeiten im Spiel, so verhindert die Formel (8) auf wunderbare Weise das Auftreten von Überlichtgeschwindigkeiten: Es lässt sich ganz allgemein zeigen, dass -c < w < c, solange -c < u < c und -c < v < c ist. Versuchen wir es mit u = v = 3c/4, so erhalten wir w = 0.96 c, was kleiner als c ist (wohingegen die galileische Rechnung auf 1.5 c, also eineinhalbfache Lichtgeschwindigkeit führen würde)!

Im Grenzfall v = c (wenn es sich nicht um eine materielle Kugel, sondern um ein Photon handelt) erhalten wir w = c, d.h. ein Teilchen (Photon), das sich im System I' mit Geschwindigkeit c bewegt, hat dann auch im Inertialsystem I die Geschwindigkeit c. Hier haben wir den mathematischen Grund, der die - in der galileischen Physik unmögliche - Konstanz der Lichtgeschwindigkeit (siehe den Abschnitt Postulate) ermöglicht.
 

So einfach und ansprechend unser zentrales Resultat, Formel (8), auch sein mag - die oben vorgeführte Herleitung ist umständlich. Die Argumentationslogik ist eine sture Anwendung der zuvor diskutierten Effekte und nicht mit tieferen Einblicken in das neue Konzept von Raum und Zeit verbunden. Demgegenüber gibt es elegantere Herleitungen - sie erfordern zwar mehr Vorbereitungsaufwand, führen aber dann schneller zum Ziel und sind theoretisch befriedigender. Wir wollen zwei dieser Argumentationen - beide benötigen Vorgriffe auf spätere Abschnitte - kurz vorstellen.

• Formel (8) kann direkt - ohne viel physikalischen Nachdenkens - aus der Form der Lorentztransformation abgeleitet werden. Dabei wird die Bewegung unseres Objekts (Kugel), wie sie sich im System I' ausnimmt, in der Form  x' = v t'  angesetzt. Dann werden die Raumzeit-Koordinaten x' und t' einer Lorentztransformation mit Geschwindigkeitsparameter u, (welches ja die Relativgeschwindigkeit zwischen I und I' darstellt) unterzogen, d.h. es wird t' durch g (t - u x/c²) und x' durch g (x - u t) ersetzt, wobei g = (1 - u²/c² )^-1/2  ist. Die entstehende Gleichung kann zu  x (1 + u v/c² ) = (u + v) t  umgeformt werden, woraus sich

  x  =  w t       mit       w  =  (u + v) (1 + u v/c2 )-1

  (9)

  für die Bewegung der Kugel im System I ergibt. Daraus folgt unmittelbar das frühere Resultat (8).
   
• Eine besonders elegante Herleitung ergibt sich aus dem Bondischen k-Kalkül, indem das folgende Raumzeit-Diagramm betrachtet wird:

  

  Dabei ist w₁ die Weltlinie eines in I ruhenden Beobachters, w₂ die Weltlinie eines in I' ruhenden Beobachters und w₃ die Weltlinie der Kugel. Die in roter Farbe eingezeichneten Eigenzeit-Intervalle stehen nach der elementaren Regel des k-Kalküls - siehe die dortige Formel (1) - in folgenden Verhältnissen:
   
  • T₂  =  k_u T₁, wobei k_u der k-Faktor mit Geschwindigkeitsparameter u ist.
  • T₃  =  k_v T₂  =  k_u k_v T₁, wobei k_v der k-Faktor mit Geschwindigkeitsparameter v ist.
  • Da sich die Kugel in I mit Geschwindigkeit w bewegt, gilt andererseits T₃  =  k_w T₁.
  
  Daher muss gelten:

  kw  =  ku kv .

  (10)

  Werden die Geschwindigkeiten w, u und v in diese Gleichung eingesetzt, entsteht (nachdem die Wurzelzeichen der k-Faktoren weggelassen werden) die Beziehung

  1 + w/c 1 - w/c  =  1 + u/c 1 - v/c 1 + v/c 1 - u/c  ,

  (11)

  und nach einigen Umformungen resultiert genau die Formel (8). In diesem Sinne kommt die relativistische Geschwindigkeitsaddition einfach durch die Multiplikation der k-Faktoren zustande.
  
  Diese Herleitung kann auch unter Zuhilfenahme des relativistischen Dopplereffekts, die mit der elementaren Regel des k-Kalküls identisch ist, physikalisch motiviert werden. (Drei Beobachter tauschen Lichtsignale aus, wobei drei Rot- bzw. Blauverschiebungsfaktoren k_u, k_v und k_w auftreten).
   

Die relativistische Geschwindigkeitsaddition hat eine interessante geometrische Deutung, die einen Blick in die tieferen Strukturen der Speziellen Relativitätstheorie ermöglicht: Die Formel (8) ist eng verwandt mit dem Satz der euklidischen Geometrie, dass die Winkelsumme in jedem Dreieck 180° beträgt! Näheres darüber kann auf der Seite

Geometrische Deutung
der relativistischen Geschwindigkeitsaddition
- eine Überraschung
(http://www.ap.univie.ac.at/users/fe/Rel/Geschwindigkeitsaddition/)

nachgelesen werden. (Zur Frage, was das Wort "geometrisch" hier bedeutet, siehe den Abschnitt über die Geometrie der Raumzeit).