Spezielle Relativitätstheorie

Dieser Abschnitt behandelt eine reizvolle Konsequenz des relativistischen Konzepts von Raum und Zeit und illustriert, wie die Lorentztransformation auf eine nicht ganz einfache Situation angewandt wird. Da er eine Überraschung bereithält, wollen wir es spannend machen und ohne Umschweife mit einer konkreten Problemstellung beginnen.

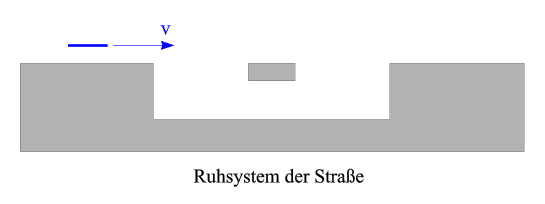
Gegeben sei eine Straße, die eine Vertiefung mit einer Verstrebung aufweist, wie die folgende Abbildung (die als Längsschnitt zu verstehen ist) illustriert:

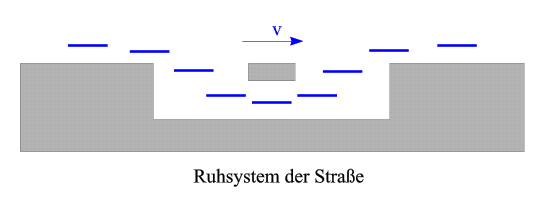
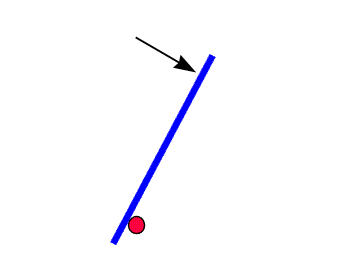
Nun findet ein Prozess statt, der im Ruhsystem der Straße folgendermaßen aussieht: Von links nähert sich ein Flugkörper, den wir einfach als blauen Strich kennzeichnen, mit Geschwindigkeit v und taucht unter der Verstrebung durch. In der nächsten Abbildung ist die Lage des Flugkörpers zu einigen Zeitpunkten gezeigt:

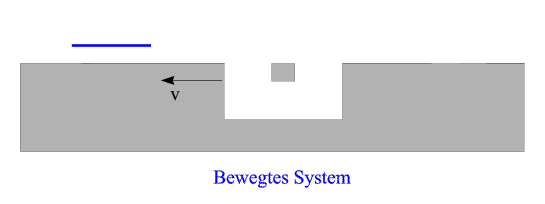
Wenn er sich der Vertiefung nähert, senkt er sich nach unten ab, taucht hindurch, steigt wieder auf und setzt seinen Weg fort. Während des gesamten Prozesses sei die horizontale Komponente seiner Geschwindigkeit nach wie vor durch v gegeben.

Nun betrachten wir ein anderes Inertialsystem - nämlich jenes, in dem der Flugkörper vor dem Abtauchen in Ruhe ist. (Da seine horizontale Geschwindigkeitskomponente immer v ist, bewegt er sich in diesem neuen System dann lediglich in vertikaler Richtung). Wir wollen es einfach das "bewegte System" nennen. Wie sieht der soeben beschriebene Prozess in diesem neuen Inertialsystem aus? Aufgrund der Lorentzkontraktion ist der Flugkörper nun länger als im System der Straße, während die Straße - insbesondere die Vertiefung - kürzer ist als in ihrem Ruhsystem. Insgesamt entsteht eine Situation wie in der nächsten Abbildung gezeigt:

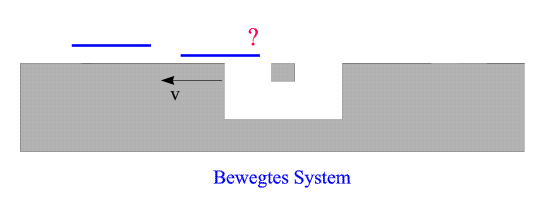
Der Flugkörper ruht, die Straße bewegt sich mit Geschwindigkeit v von rechts an ihm vorbei, und die Vertiefung kommt näher. Allerdings scheint sie nun zu klein zu sein: der Flugkörper kann nicht durchtauchen, da er zu lang ist - er passt nicht hinein!

Das ist eine unangenehme Situation: Ob der Flugkörper unter der Verstrebung durchtauchen kann, sollte eigentlich nicht vom Bezugssystem abhängen, in dem dieser Prozess beschrieben wird! Wurde in der obigen Argumentation etwa ein Fehler gemacht? Wie sieht der Prozess des Durchtauchens - der im Ruhsystem der Straße ja ohne jedes Problem vor sich geht - im bewegten System tatsächlich aus? Denken Sie zunächst ein bisschen über dieses Problem nach, bevor Sie weitergehen...

...und die Aufösung aufrufen.
 

Was ist passiert? Nun, eigentlich hat ja niemand versprochen, dass ein Objekt, das in einem Inertialsystem ein geradliniges Objekt ist, diesen Charakter auch in jedem anderen Inertialsystem beibehält. Wenn das Objekt nicht beschleunigt ist, sich also alle seiner Punkte - in einem Inertialsystem - mit derselben (konstanten) Geschwindigkeit bewegen, dann ist es in jedem Inertialsystem eine gerade Linie. Treten aber Beschleunigungen auf (wie im obigen Paradoxon), so kann das Objekt in einem anderen Inertialsystem seine Geradlinigkeit einbüßen. Es ist eine schöne Anwendung der Formeln der Lorentztransformation, diesen Sachverhalt anhand eines Beispiels durchzurechnen:

Stellen wir uns ein Objekt vor, das (in einem Inertialsystem I) eine zur x-Achse parallele Linie in der (x y)-Ebene darstellt. (Die z-Koordinate wollen wir ganz ignorieren. Wer will, kann sie 0 setzen). Nun werden alle seine Punkte gleichzeitig in y-Richtung beschleunigt. (Das entspricht der Abwärts- und der Aufwärtsbewegung des Flugkörpers im obigen Paradoxon, wobei wir uns hier allerdings nicht damit aufhalten wollen, seine Länge zu begrenzen). Der Einfachheit halber wollen wir dabei die (nichtrelativistische) gleichmäßige Beschleunigung annehmen und dabei das Problem ausser acht lassen, dass nach genügend langer Zeit die Lichtgeschwindigkeit überschritten wird.

Die Gleichung, die diese Bewegung beschreibt, lautet:

Jedes Ereignis mit Raumzeit-Koordinaten (t, x, y), das diese Gleichung erfüllt, ist ein Ereignis auf unserem Objekt! Zu einer gegebenen Zeit t ist das Objekt eine Gerade, weil seine Gleichung einfach  y = const  lautet (t kann zu einer fixierten Zeit ja als Konstante behandelt werden).

Nun betrachten wir denselben Prozess in einem Inertialsystem I', das sich gegenüber I mit Geschwindigkeit v in x-Richtung bewegt. Dazu unterwerfen wir die Raumzeit-Koordinaten der Lorentztransformation

wobei

ist. Indem wir einfach (2a) und (2c) in (1) einsetzen, erhalten wir

Das ist die Gleichung, die den Prozess im System I' beschreibt. Jedes Ereignis mit Raumzeit-Koordinaten (t', x', y') - bezüglich I' -, das diese Gleichung erfüllt, ist ein Ereignis auf unserem Objekt!

Sehen wir uns Gleichung (4) näher an. Fixieren wir eine Zeit t' und behandeln t' und v als Konstante. Dann hat (4) die Struktur

wobei c₁ und c₂ Konstante sind. Solange die Beschleunigung a und die Geschwindigkeit v von Null verschieden sind, sind auch die beiden Konstanten von Null verschieden, und in diesem Fall ist (5) die Gleichung einer Parabel! Unser "geradliniges Objekt" ist im Inertialsystem I' also eine Parabel.

Mathematisch gesehen ist das eine unmittelbare Konsequenz der Lorentztransformation: Die Parabelform rührt daher, dass in der Bewegungsgleichung (1) ein Quadrat der Zeit auftritt. Die Lorentztransformation "mischt" Raum- und Zeitkoordinaten in linearer Weise, sodass im System I' das Quadrat einer räumlichen Koordinate (nämlich von x') auftritt. In diesem Sinn übersetzt sich der zeitliche Verlauf einer Koordinate in Formel (1) in die räumliche Form einer Kurve in Formel (5).
 

Diese Betrachtungen sind nicht nur von akademischem Interesse - sie zeigen, in welchem Ausmaß Begriffe und Verfahren der galileischen Physik aufgegeben oder verändert werden müssen. Wir wollen zum Abschluss noch auf zwei verwandte Probleme eingehen.

Zunächst ist die Form eines Körpers abhängig vom Inertialsystem, in dem sie vermessen wird. Ist der Körper beschleunigt, so treten zur Verkürzung durch die Lorentzkontraktion noch Effekte der eben besprochenen Art hinzu. So lässt sich etwa von einem beschleunigten Objekt gar nicht eindeutig sagen, ob es ein Würfel ist, denn die Geradlinigkeit seiner Kanten mag nur in manchen Inertialsystemen (oder in gar keinem) gegeben sein.

Und dann kommt ein weiteres wichtiges Konzept ins Wanken: Die Geradlinigkeit eines materiellen Objekts ist verwandt mit der Idee des starren Körpers, d.h. eines Körpers, der allen Versuchen, ihn zu verbiegen, trotzt, und der seine Form immer beibehält. In der Aufklärung des obigen Paradoxons wird klar, dass auf das Flugobjekt im bewegten System Kräfte wirken, die es verbiegen. (Im Ruhsystem der Straße sind diese nicht so offensichtlich). Mit der Beschleunigung ausgedehnter materieller Objekte treten also durchaus Kräfte auf, die man nicht erwartet hätte. Kann es sich bei dem Flugobjekt etwa um einen starren Körper handeln, der allen Verbiegungsversuchen widersteht? Das ist schwer vorstellbar, da es bedeuten würde, dass das Objekt nicht einmal im Ruhsystem der Straße zu seiner Bewegung (die ja lediglich in einer gleichzeitigen und identischen Beschleunigung aller seiner Punkte besteht) gezwungen werden kann, da sie vom bewegten System aus betrachtet mit einer Verbiegung einhergehen müßte.

Tatsächlich kann es einen starren Körper im Rahmen der Speziellen Relativitätstheorie nicht geben. Ein solcher würde sogar in einem einzigen Inertialsystem Probleme machen. Hier zwei Beispiele, die das belegen:

• Dieses Beispiel zeigt auf sehr einfache Weise, dass die Geradlinigkeit eines materiellen Objekts ein heikles Konzept ist:

  

  Ein Stab liege, wie in der Abbildung gezeigt, an einer Rolle (in rot dargestellt) auf, ist aber ansonsten nicht an ihr fixiert. Zunächst sei er in Ruhe. Wird er dann am anderen Ende in Pfeilrichtung bewegt, so kann er sich nicht auf seiner gesamten Länge starr verdrehen, da ansonsten die Information, dass an ihm manipuliert wird, sogleich (mit "unendlicher Geschwindigkeit", wenn man so will) am gegenüberliegenden Ende ankommt. Andererseits gibt es keinen Grund, warum er einer solchen Krafteinwirkung nicht nachgeben sollte. Während ein Ende des Stabes bereits verdreht ist, ist das andere (zumindest für kurze Zeit) noch in der ursprünglichen Richtung orientiert. Mit anderen Worten: Der Stab muss sich verbiegen, ganz gleich, welche inneren Kräfte in ihm wirken und versuchen, ihn starr zu halten!
   
• Ein ähnlich gelagertes Beispiel, dass die Starrheit ausschliesst, selbst wenn nur eine einzige Raumdimension beteiligt ist: Wenn auf ein Ende eines (zunächst ruhenden) Stabes eine Kraft einwirkt, um ihn in Längsrichtung zu bewegen (z.B. ein Hammerschlag), so kann er sich nicht starr vorwärtsbewegen, da ansonsten die Information, dass an ihm manipuliert wird, sogleich (wieder mit "unendlicher Geschwindigkeit") am gegenüberliegenden Ende ankommt. Da es andererseits keinen Grund gibt, warum er als Ganzes der Krafteinwirkung nicht nachgeben sollte, muss sich das eine Ende in Bewegung setzen, während das andere noch ruht! Der Stab wird unausweichlich zusammengedrückt.

Um das Verhalten ausgedehnter beschleunigter Körper in der Speziellen Relativitätstheorie genauer zu studieren, sind konkrete Modelle der Kräfte, die in ihnen wirken, notwendig. Wir wollen es aber bei diesen Anregungen belassen.