|
|
|
||||||||
|
|
||||||||
|
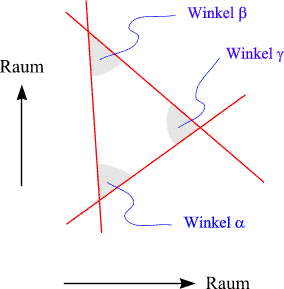
Jede Gerade repräsentiert eine Richtung. Die relativen Richtungen zweier Geraden zueinander werden durch den Winkel, den sie miteinander einschließen, ausgedrückt. |
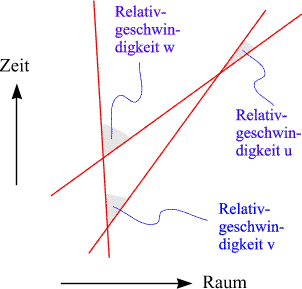
Jede Weltlinie repräsentiert den Bewegungszustand eines kräftefreien Beobachters (Inertialsystems). Die relativen Bewegungszustände zweier solcher Beobachter werden durch die Geschwindigkeit ausgedrückt, mit der sich der eine, vom Inertialsystem des anderen aus gemessen, bewegt. |
||||||||
|
Wir betrachten ein Dreieck wie in der obigen Skizze abgebildet.
Zwei der Winkel können vorgegeben werden,
der dritte ist dann bereits eindeutig festgelegt.
Sind a und b
vorgegeben, so bestimmt sich g
aus der Gleichung
a + b + g = p oder, verbal ausgedrückt: Die Winkelsumme im Dreieck beträgt 180°. Dabei bilden die drei Winkel, wie oben eingezeichnet, die Innenwinkel des Dreiecks. |
Wir betrachten drei Weltlinien, die zueinander liegen wie in der obigen Skizze.
Zwei der Relativgeschwindigkeiten können vorgegeben werden,
die dritte ist dann bereits eindeutig festgelegt.
Sind v und
w
vorgegeben, so bestimmt sich
u
aus der Gleichung
|
||||||||
| Die Situation hat eine einfache operative Bedeutung: Zieht man von einer Geraden zwei zweitere Geraden unter den Winkeln a und b (wie in der obigen Skizze), so schneiden diese beiden Geraden einander unter dem Winkel g. | Die Situation hat eine einfache physikalische Bedeutung: Stellen Sie sich vor, sie sind der Beobachter mit der steilsten Weltlinie und schiessen ein Raumschiff mit der Geschwindigkeit v von Ihnen weg. Einige Zeit später schießen Sie ein weiteres Raumschiff mit der - größeren - Geschwindigkeit w dem ersten nach. Dann ist u die im Inertialsystem des langsameren Raumschiffs gemessene Geschwindigkeit, mit der es vom schnelleren überholt wird. Die drei vorkommenden Geschwindigkeiten können jeweils in unmittelbarer Nähe der drei Ereignisse gemessen werden, die den Schnittpunkten der drei Weltlinien entsprechen. | ||||||||
Die relative Lage zweier Geraden kann anstelle des (Innen-)Winkels
durch dessen Tangens ausgedrückt werden. Um ihn zu messen,
wird das Dreieck so gedreht, dass eine Gerade parallel zur
x-Achse ist.
Der Tangens des Winkels ist dann gerade der Anstieg der anderen
Geraden:
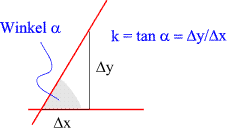 Wird k' = tan b k'' = tan g
Wird im obigen Dreieck anstelle des Innenwinkels b der Supplementärwinkel b' = p - b verwendet, so lautet der Satz über die Winkelsumme im Dreieck nun g = b' - a, und das rätselhafte p ist verschwunden. |
Zeichnet ein Beobachter ein zu seinem Inertialsystem gehörendes
Raumzeit-Diagramm
(d.h. seine Weltlinie fällt mit der t-Achse
zusammen), so stellt sich die Geschwindigkeit, mit der
sich ein anderer Beobachter bewegt, als Kehrwert des Anstiegs
dessen Weltlinie dar:
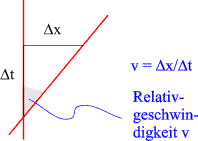 Die Relativgeschwindigkeit v ist also in formal ähnlicher Weise definiert wie die in der linken Spalte verwendete Größe k, der Tangens des Winkels a zwischen zwei Geraden. Anstelle der Geschwindigkeit kann aber auch eine dem Winkel entsprechende Größe verwendet werden: Wird w = tanh c u = tanh y y = c - f an, hat also formal eine ganz ähnliche Struktur wie der Satz über die Winkelsumme im Dreieck. (Der verbleibende Unterschied rührt daher, dass die Definition der Relativgeschwindigkeit u im obigen Diagramm eher dem Außenwinkel als dem Innenwinkel eines Dreiecks entspricht. Verwendet man - wie im letzten Absatz der linken Spalte vorgeführt - im euklidischen Dreieck anstelle des Innenwinkels b seinen Supplementärwinkel b', so verschwindet das rätselhafte p, und die Analogie zwischen der relativistischen Geschwindigkeitsaddition und dem Satz über die Winkelsumme im Dreieck ist perfekt! Dass in der obigen Rechnung nicht der Tangens, sondern der Tangens hyperbolicus verwendet wird, widerspiegelt den Unterschied zwischen der euklidischen und der Lorentz-Geometrie). Dieses Resultat zeigt eine (auf den ersten Blick "verborgene") lineare Struktur hinter der Geschwindigkeitsaddition auf. |
||||||||
Mathematische Nachbemerkung:
Der obigen Berechnung liegt folgende Eigenschaft der Tangensfunktion
zugrunde:
|
Mathematische Nachbemerkung:
Der obigen Berechnung liegt folgende Eigenschaft der Funktion
Tangens hyperbolicus zugrunde:
|