|
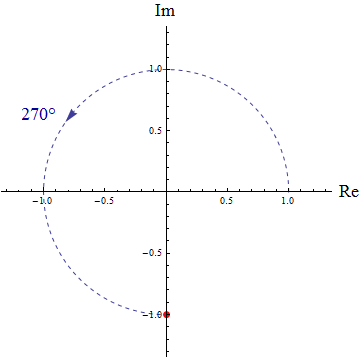
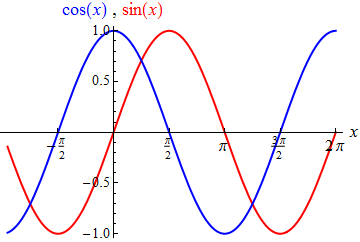
Aufgabe: Berechnen Sie Real- und Imaginärteil der komplexen Zahl $z=e^{3\pi i/2}$ ! Berechnung: Wir verwenden die Eulersche Formel $$e^{i\,x}=\cos x+i\,\sin x$$ und finden $z=\cos\left(3\pi\over2\right)+i\,\sin\left(3\pi\over2\right)$, also $$\begin{eqnarray} {\rm Re}(z) &=& \cos\left(3\pi\over2\right)\\ {\rm Im}(z) &=& \sin\left(3\pi\over2\right) \end{eqnarray}$$ Fertig! Fertig? Nein – nicht fertig! Die angegebene Form von $z$ ist zwar nicht falsch, aber sie als Ergebnis stehen zu lassen wäre so, als würden Sie die Berechnung von ${2\over 5}+{3\over 3}$ mit dem "Ergebnis" $2+3\over 5$ gut sein lassen! $\cos\left(3\pi\over2\right)$ und $\sin\left(3\pi\over2\right)$ haben konkrete und "schöne" Zahlenwerte, nämlich $\cos\left(3\pi\over2\right)=0$ und $\sin\left(3\pi\over2\right)=-1$. Wie auch immer Sie es anstellen, sie zu bestimmen – ohne ihre Angabe ist die Aufgabe nicht wirklich gelöst. Die Lösung lautet daher $$\begin{eqnarray} {\rm Re}(z) &=& 0\\ {\rm Im}(z) &=& -1 \end{eqnarray}$$ Nachbemerkung: Zwei Möglichkeiten, die Werte von $\cos\left(3\pi\over2\right)$ und $\sin\left(3\pi\over2\right)$ zu bestimmen:
|