Faßt man die mikroskopischen Variablen als Koordinaten in einem
hochdimensionalen
Raum auf, dann ist der mikroskopische Zustand des Systems durch einen
Punkt oder Vektor in diesem Raum repräsentiert. Der Raum wird als
Gibbsscher Phasenraum oder Zustandsraum bezeichnet; für den
Zustandsvektor verwendet man meist das Symbol ![]() .
.
Der Zustandsvektor eines klassischen Vielteilchensystems aus isotropen
Teilchen - also eines idealen Gases, eines Fluids aus harten Kugeln
oder LJ-Molekülen usw. - ist durch die Angabe aller Örter und
Geschwindigkeiten vollständig bestimmt:
| (3.1) |
Diese Darstellung des Mikrozustandes eines ganzen Systems durch einen
einzigen Punkt im ![]() -dimensionalen Gibbsschen Phasenraum ist zu
unterscheiden von der in Kapitel 2 eingeführten Behandlung, die auf
Boltzmann zurückgeht. Der dort definierte
-dimensionalen Gibbsschen Phasenraum ist zu
unterscheiden von der in Kapitel 2 eingeführten Behandlung, die auf
Boltzmann zurückgeht. Der dort definierte ![]() -Raum weist nur
-Raum weist nur ![]() Dimensionen
Dimensionen
![]() auf; jedem Teilchen eines Systems entsprach in
dieser Darstellung ein Punkt, und der Mikrozustand eines Systems
aus
auf; jedem Teilchen eines Systems entsprach in
dieser Darstellung ein Punkt, und der Mikrozustand eines Systems
aus ![]() Teilchen
wurde durch eine Schar von
Teilchen
wurde durch eine Schar von ![]() Punkten
Punkten
![]() repräsentiert.
repräsentiert.
Im Fall des quantenmechanischen idealen Gases genügt die Angabe aller
Quantenzahlen zur Festlegung des Zustandes:
| (3.2) |
| (3.3) |
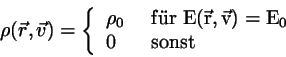 |
(3.4) |
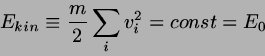 |
(3.5) |
Eine typische Frage, die durch Anwendung statistischer Methoden auf eine
solche Gesamtheit zu beantworten ist, lautet: wie groß der Mittelwert
des Quadrats der Teilchengeschwindigkeit
![]() über alle - a priori gleich wahrscheinlichen - Zustände
auf dieser Energiefläche?
über alle - a priori gleich wahrscheinlichen - Zustände
auf dieser Energiefläche?
ERGODENHYPOTHESE
Anstelle einer Gesamtheit von Systemen betrachten wir nun ein einziges
System; dieses soll sich aber nach den Gesetzen der Mechanik in
der Zeit entwickeln. In einem abgeschlossenen System bleibt die
Gesamtenergie ![]() erhalten; die Mikrozustände, die das System
im Lauf der Zeit durchläuft, liegen also durchwegs auf der
erhalten; die Mikrozustände, die das System
im Lauf der Zeit durchläuft, liegen also durchwegs auf der
![]() -dimensionalen Energieschale, die auch das mikrokanonische
Ensemble definiert.
-dimensionalen Energieschale, die auch das mikrokanonische
Ensemble definiert.
Die Ergodenhypothese besagt, daß bei dieser ,,natürlichen Entwicklung`` des Systems jeder erlaubte Mikrozustand im Lauf der Zeit erreicht (bzw. beliebig nahe approximiert) wird, und zwar mit gleicher relativer Häufigkeit.
Diese Hypothese kann nicht allgemein bewiesen werden; sie gilt auch
nicht in jedem Fall. Für viele relevante Systeme, wie z.B. Gase oder
Flüssigkeiten unter normalen Bedingungen, ist sie aber gut erfüllt.
Die Zeitspanne ![]() , die zum ausreichenden Durchstreifen der
Energiefläche nötig ist, liegt dann im Bereich von
, die zum ausreichenden Durchstreifen der
Energiefläche nötig ist, liegt dann im Bereich von
![]() Sekunden, also weit unter einer typischen experimentellen
Beobachtungsdauer. Zu jenen Systemen, die ,,schlecht ergodisch`` oder nicht-ergodisch sind, gehören unterkühlte Flüssigkeiten
sowie Gläser. Bei solchen Systemen bleibt der Zustandsvektor
Sekunden, also weit unter einer typischen experimentellen
Beobachtungsdauer. Zu jenen Systemen, die ,,schlecht ergodisch`` oder nicht-ergodisch sind, gehören unterkühlte Flüssigkeiten
sowie Gläser. Bei solchen Systemen bleibt der Zustandsvektor
![]() lange in einem Teilbereich der Energiefläche gefangen und findet
erst nach Sekunden, Tagen oder gar Jahrhunderten den Weg zu anderen
Teilen der mikrokanonischen Zustandsfläche.
lange in einem Teilbereich der Energiefläche gefangen und findet
erst nach Sekunden, Tagen oder gar Jahrhunderten den Weg zu anderen
Teilen der mikrokanonischen Zustandsfläche.
Die Ergodenhypothese hat eine wichtige praktische Konsequenz: Bei der
Ermittlung von Mittelwerten über die auf der Energiefläche liegenden
Mikrozustände ist es gleichgültig, ob man über die ![]() Systeme
des mikrokanonischen Ensembles mittelt oder den zeitlichen Mittelwert
über die nacheinander auftretenden Mikrozustände eines einzigen isolierten
Systems bildet. Dieses Korollar der Ergodenhypothese wird oft auf
die Kurzformel
Systeme
des mikrokanonischen Ensembles mittelt oder den zeitlichen Mittelwert
über die nacheinander auftretenden Mikrozustände eines einzigen isolierten
Systems bildet. Dieses Korollar der Ergodenhypothese wird oft auf
die Kurzformel
Die Ergodenhypothese erlaubt uns, im folgenden zur Unterstützung der
theoretischen Argumente auch Computersimulationen heranzuziehen.
Dabei handelt es sich bis auf weiteres um
deterministische Simulationen, also um die möglichst genaue
Berechnung der zeitlichen Entwicklung eines einzigen isolierten Systems;
man spricht in diesem Zusammenhang auch von
Molekulardynamik-Simulation.
(Eine andere Art von Simulationen, die sogenannte Monte Carlo-Rechnung,
durchstreift stattdessen den Zustandsraum in stochastischer Weise; die
verschiedenen Mikrozustände werden dabei von vornherein mit der ihnen
zukommenden relativen Häufigkeit aufgesucht.)
ENERGIESCHALE
Anstelle der strikten Bedingung ![]() werden wir im
allgemeinen die schwächere Bedingung
werden wir im
allgemeinen die schwächere Bedingung
![]()
![]()
![]() betrachten. Die Zustände des Systems sollen also auf
eine dünne ,,Schale`` bei
betrachten. Die Zustände des Systems sollen also auf
eine dünne ,,Schale`` bei
![]() beschränkt sein.
Diese Bedingung
entspricht der realistischen Annahme, daß der Energieaustausch
zwischen einem System und seiner Umgebung zwar nicht völlig
unterdrückt, aber doch klein gehalten werden kann.
beschränkt sein.
Diese Bedingung
entspricht der realistischen Annahme, daß der Energieaustausch
zwischen einem System und seiner Umgebung zwar nicht völlig
unterdrückt, aber doch klein gehalten werden kann.
Für die Dichte im Phasenraum soll also nun gelten
![\begin{displaymath}
\rho(\vec{r},\vec{v}) = \left\{ \begin{array}{ll} \rho_{0} \...
...}, \Delta E \right] \\
0 \; & {\rm sonst}
\end{array} \right.
\end{displaymath}](img541.png) |
(3.6) |
Eine Übersicht über die Zustandsräume und Energien
der verschiedenen Modellsysteme ist aus Tabelle 3.1
zu ersehen.
Daraus folgt aber, daß ein Makrozustand, der mehr Mikrozustände zuläßt als ein anderer, auch häufiger auftritt - und somit wahrscheinlicher ist.
Um ein konkretes Beispiel anzuführen, fragen wir nach der
Wahrscheinlichkeit, mit der alle Moleküle eines idealen Gases in der
linken Hälfte eines Gefässes aufzufinden sein werden, wobei sie im übrigen
alle möglichen Positionen und Geschwindigkeiten annehmen mögen.
Alle so definierten Mikrozustände liegen in einem Teil der
gesamten ,,zugelassenen`` Phasenraum-Kugelschale ![]() ; sie
bilden ein Subensemble der vollständigen mikrokanonischen Gesamtheit.
Die Wahrscheinlichkeit der Situation ,,alle Teilchen in der linken
Hälfte des Behälters`` ist offenbar gleich dem Größenverhältnis
zwischen dem Subensemble und dem vollständigen Ensemble. Es wird daher
notwendig sein, das Teilvolumen der Phasenraum-Kugelschale, das zum
Subensemble gehört, mit dem Volumen der gesamten Kugelschale zu vergleichen.
(Später wird sich herausstellen, daß das Verhältnis der beiden PR-Volumina
gleich
; sie
bilden ein Subensemble der vollständigen mikrokanonischen Gesamtheit.
Die Wahrscheinlichkeit der Situation ,,alle Teilchen in der linken
Hälfte des Behälters`` ist offenbar gleich dem Größenverhältnis
zwischen dem Subensemble und dem vollständigen Ensemble. Es wird daher
notwendig sein, das Teilvolumen der Phasenraum-Kugelschale, das zum
Subensemble gehört, mit dem Volumen der gesamten Kugelschale zu vergleichen.
(Später wird sich herausstellen, daß das Verhältnis der beiden PR-Volumina
gleich ![]() , also verschwindend klein ist - im Einklang mit
Erfahrung und Intuition.)
, also verschwindend klein ist - im Einklang mit
Erfahrung und Intuition.)