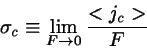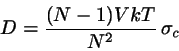

To determine the diffusion constant  Ciccotti et al.
[J. Stat. Phys. 21(1979)1] suggest the following Hamiltonian
non-equilibrium method:
Ciccotti et al.
[J. Stat. Phys. 21(1979)1] suggest the following Hamiltonian
non-equilibrium method:
Let
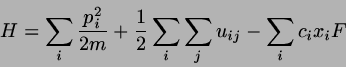 |
(8.43) |
where 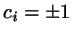 for even/odd numbered particles is a
``color charge'' coupling to the applied ``color field''
for even/odd numbered particles is a
``color charge'' coupling to the applied ``color field'' 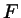 .
.
In other words, particles are drawn in opposite directions depending
on their number; otherwise, they are completely identical.
Keeping 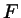 constant we have
constant we have
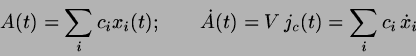 |
(8.44) |
where 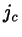 is the ``color current''.
is the ``color current''.
Again, the external field does work on the system, heating it:
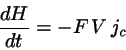 |
(8.45) |
The heating may once more be avoided by Gaussian terms in the eqs. of
motion which now read, in 2 dimensions,
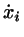 |
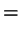 |
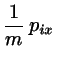 |
(8.46) |
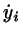 |
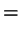 |
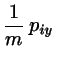 |
(8.47) |
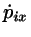 |
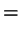 |
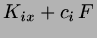 |
(8.48) |
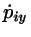 |
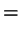 |
![$\displaystyle K_{iy} \;\;\;\;\;\;\;\;\;\;[- \frac{\lambda}{m}p_{iy}]$](img608.png) |
(8.49) |
In this way a ``color conductivity''
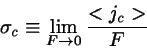 |
(8.50) |
may be evaluated. Applying Linear Response Theory one may show that
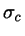 is closely related to the diffusion constant:
is closely related to the diffusion constant:
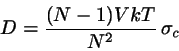 |
(8.51) |

 F. J. Vesely / University of Vienna
F. J. Vesely / University of Vienna
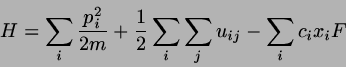
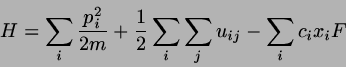
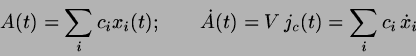
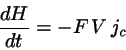
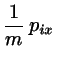
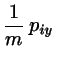
![$\displaystyle K_{iy} \;\;\;\;\;\;\;\;\;\;[- \frac{\lambda}{m}p_{iy}]$](img608.png)