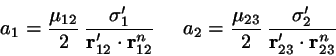Lagrange constraint forces: keep the bond lengths constant.
The constraint force on atom ![]() is parallel to
is parallel to
![]() .
Atom
.
Atom ![]() is subject to two constraint forces along
is subject to two constraint forces along
![]() and
and
![]() . Atom
. Atom ![]() is kept in line by
a force along
is kept in line by
a force along
![]() :
:
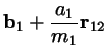 |
|||
![$\displaystyle \mbox{$\bf b$}_{2}+\frac{1}{m_{2}}
\left[-a_{1}\mbox{$\bf r$}_{12}+a_{2}\mbox{$\bf r$}_{23}\right]$](img244.png) |
|||
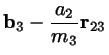 |
Instead of solving these two quadratic equations for the unknowns ![]() we ignore, for the time being, the small quadratic terms.
The remaining linear equations are solved iteratively,
meaning that this system
of linear equation is solved to arrive at an improved estimate
for
we ignore, for the time being, the small quadratic terms.
The remaining linear equations are solved iteratively,
meaning that this system
of linear equation is solved to arrive at an improved estimate
for ![]() which is again inserted in 4.1-4.3
leading to a new set of linearized equations etc., until the absolute
values of
which is again inserted in 4.1-4.3
leading to a new set of linearized equations etc., until the absolute
values of ![]() are negligible; generally, this will occur after a very
few iterations.
are negligible; generally, this will occur after a very
few iterations.
Solving the linearized equations involves a matrix inversion.
To avoid this we introduce one more simplification:
In passing through the chain from one end to the other
we consider only one constraint per atom: