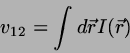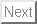
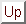

0.1 DFT for HSC/HS mixtures
My suggestion is to take a somewhat simplified version
of Velasco/Mederos/Sullivan (VMS) and generalize it to
mixtures.
The central equation in VMS is (their equ. 23)
![\begin{displaymath}
\phi^{ex}[\rho_{1}]= \frac{1}{v_{11}} \frac{1}{d}
\int_{0}^{...
...{1}(z')
\tilde{v}_{11} \left(z-z';(\eta(z)+\eta(z'))/2 \right)
\end{displaymath}](img1.png) |
(1) |
where I use the notation
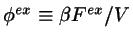 for
the reduced excess free energy density. The meaning of the various terms is
as follows:
for
the reduced excess free energy density. The meaning of the various terms is
as follows:
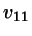 ... excluded volume between two representative hard ellipsoids; these
are defined as ellipsoids with the same volume and aspect ratio (total)
as the given HSC; the ellipsoids may be transformed into representative
spheres with the same volume (to be used in Carnahan-Starling)
... excluded volume between two representative hard ellipsoids; these
are defined as ellipsoids with the same volume and aspect ratio (total)
as the given HSC; the ellipsoids may be transformed into representative
spheres with the same volume (to be used in Carnahan-Starling)
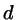 is the period of an eventual smectic density wave; since the system is
either homogeneous or periodic along
is the period of an eventual smectic density wave; since the system is
either homogeneous or periodic along 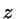 we may use
we may use 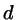 as the total system
length
as the total system
length
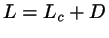 ... total length of the HSC, with
... total length of the HSC, with  the cylinder length,
and
the cylinder length,
and 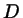 the cap diameter
the cap diameter
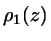 ... number density of the HSC fluid as a function of
... number density of the HSC fluid as a function of 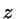
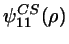 ... reduced excess free energy per particle
for a fluid of representative spheres, at some density
... reduced excess free energy per particle
for a fluid of representative spheres, at some density 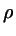 , as given
by Carnahan and Starling
, as given
by Carnahan and Starling
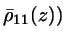 ... weighted density of the HSC fluid; here
we will simplify matters by assuming only a basic weighting function
... weighted density of the HSC fluid; here
we will simplify matters by assuming only a basic weighting function
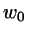 (see below)
(see below)
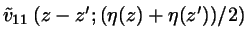 ... effective
potential acting on the HSC fluid at
... effective
potential acting on the HSC fluid at 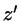 if a HSC is situated at
if a HSC is situated at
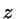 ;
;
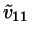 has the dimension of an area
has the dimension of an area
A natural extension to mixtures of HSC (number fraction X) and HS is
![\begin{displaymath}
\phi^{ex}[\rho_{1},\rho_{2}]= X^{2} \phi_{11}^{ex}[\rho_{...
...2}^{ex}[\rho_{1},\rho_{2}] +
(1-X)^{2}\phi_{22}^{ex}[\rho_{2}]
\end{displaymath}](img17.png) |
(2) |
where the first and third terms refer to the HSC and HS components,
respectively and the cross term pertains to the interaction between
HSC and HS.
I have implicitely supposed that 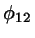 and
and 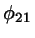 are
equal. I am not sure about that yet, but if not, it may be possible to
symmetrize the various terms (see below).
are
equal. I am not sure about that yet, but if not, it may be possible to
symmetrize the various terms (see below).
For the cross-term I assume
![\begin{displaymath}
\phi_{12}^{ex}[\rho_{1},\rho_{2}] =
\frac{1}{v_{12}} \frac{1...
...L/2}dz' \rho_{2}(z')
\tilde{v}_{12} \left(z-z';\eta(z) \right)
\end{displaymath}](img20.png) |
(3) |
where
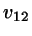 ... excluded volume between an ellipsoid representing the HSC
and a HS;
... excluded volume between an ellipsoid representing the HSC
and a HS; 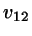 is symmetric in
is symmetric in 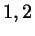
 ... number densities of HSC and HS
... number densities of HSC and HS
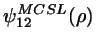 ... reduced excess free energy per particle
for a mixture of spheres, one species representing the HSC as above, the
other being the given HS. The formulae given by Mansoori, Carnahan,
Starling and Leland will be used
... reduced excess free energy per particle
for a mixture of spheres, one species representing the HSC as above, the
other being the given HS. The formulae given by Mansoori, Carnahan,
Starling and Leland will be used
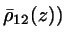 ... weighted density of the mixture
... weighted density of the mixture
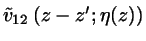 ... effective
potential acting on the SP component at
... effective
potential acting on the SP component at 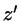 if a HSC is situated at
if a HSC is situated at
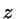 ; this must be symmetric, or symmetrized in some way, or else the terms
; this must be symmetric, or symmetrized in some way, or else the terms
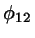 and
and 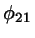 must be treated separately
must be treated separately
Now for the exact definitions:
Representative ellipsoid:
As in VMS, we choose the long and short axes
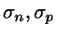 of
the ellipsoid such that the ellipsoidal volume equals
of
the ellipsoid such that the ellipsoidal volume equals
 , and the aspect ratio
, and the aspect ratio
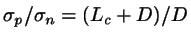 . This yields ...
. This yields ...
Excluded volume:
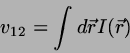 |
(4) |
(continued...)

 F. J. Vesely / University of Vienna
F. J. Vesely / University of Vienna
![\begin{displaymath}
\phi^{ex}[\rho_{1}]= \frac{1}{v_{11}} \frac{1}{d}
\int_{0}^{...
...{1}(z')
\tilde{v}_{11} \left(z-z';(\eta(z)+\eta(z'))/2 \right)
\end{displaymath}](img1.png)
![\begin{displaymath}
\phi^{ex}[\rho_{1}]= \frac{1}{v_{11}} \frac{1}{d}
\int_{0}^{...
...{1}(z')
\tilde{v}_{11} \left(z-z';(\eta(z)+\eta(z'))/2 \right)
\end{displaymath}](img1.png)
![\begin{displaymath}
\phi_{12}^{ex}[\rho_{1},\rho_{2}] =
\frac{1}{v_{12}} \frac{1...
...L/2}dz' \rho_{2}(z')
\tilde{v}_{12} \left(z-z';\eta(z) \right)
\end{displaymath}](img20.png)