| |
LENNARD-JONES LINES?
|
| |
-
Definition:
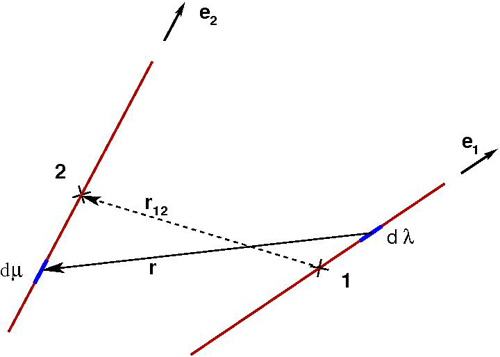
Consider two lines of finite length $L$ containing a
homogeneous density
of LJ centers. Let $\vec{e}_{1,2}$ be the direction vectors,
$\vec{r}_{12}$ the vector between the centers of the two line
segments, and $\lambda, \, \mu$ parameters giving the positions of
the interacting points along $1$ and $2$. The squared distance between
any two such points is given by
$r^{2}= \left| r_{12}+\mu \vec{e}_{2}-\lambda \vec{e}_{1} \right|^{2}$.
The total interaction energy between the two lines is then
$
u(\vec{r}_{12},\vec{e}_{1},\vec{e}_{2}) =
\frac{\textstyle 1}{\textstyle L^{2}}
\int \limits_{1} d\lambda \int \limits_{2} d\mu \, \,
u_{LJ} ( r )
$
with $u_{LJ}(r)=4 \,(r^{-12}-r^{-6})$.
|
|
| |
Let's try:
-
At fixed $\lambda$ the ($r^{-6}$) integral over $\mu$ is
$
I^{-}(\vec{r}_{12},\vec{e}_{1},\vec{e}_{2},\lambda) =
\int \limits_{-h}^{h}d\mu
\,
\left| r_{12}+\mu \vec{e}_{2}-\lambda \vec{e}_{1} \right|^{-6}
$
where $h$ is the half length of the stick.
-
Find the "proxy points" of shortest relative distance
$r_{0}$ on the two carrier lines.
-
Using new parameters $\gamma$, $\delta$ originating at the
proxy points we have
$
I^{-}(\gamma) =
\int \limits_{\delta_{a}}^{\delta_{b}}d\delta
\, \left[ \delta^{2}+p \delta + q^{2} \right]^{-3}
$
where $\delta_{b,a}=-\mu_{0} \pm h$, $p=-2 \gamma \rho$, and
$q^{2}=\gamma^{2}+r_{0}^{2}$; the correlation $\rho$ is
just the scalar product of the direction vectors,
$ \rho = e_{1} \cdot e_{2}$.
-
There is in fact an analytic solution to this:
$
\begin{eqnarray}
I^{-}(\gamma) &=&
\left[
3 \,
\frac{p+2\delta}{(4q^{2}-p^{2})^{2}[q^{2}+\delta(p+\delta)]}
+\frac{1}{2} \,
\frac{p+2\delta}{(4q^{2}-p^{2})[q^{2}+\delta(p+\delta)]^{2}}
\right.
\\
&&
\left.
+\frac{12}{(4q^{2}-p^{2})^{5/2}}
\arctan \frac{p+2\delta}{(4q^{2}-p^{2})^{1/2}}
\right]_{\delta=\delta_{a}}^{\delta=\delta_{b}}
\end{eqnarray}
$
-
However, the second integration in
$
I^{\pm} \equiv
\int \limits_{\gamma_{a}}^{\gamma_{b}} d\gamma \, I^{\pm}(\gamma)
$
with $\gamma_{b,a}=-\lambda_{0} \pm h$
can in general
not
be performed in closed form.
|
This is what happens when we try ...
|
|
|
| |
|
But then again...
|
|

(Thanks to J. Auersperg)
|
|
|
vesely nov-2006
|
|