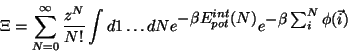

Next: 1.2 Functional Differentiation
Up: 1. Basics
Previous: 1. Basics
1.1 Functionals in Statistical Thermodynamics

Hamiltonian
of an inhomogeneous system of  particles:
particles:
where
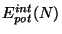 denotes the interaction energy (e. g.
denotes the interaction energy (e. g.
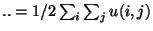 ) and
) and
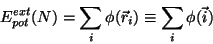 |
(1.1) |
is the energy due to an external potential.
Symmetry breaking: either by
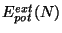 in the Hamiltonian,
or - even for
in the Hamiltonian,
or - even for
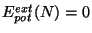 - by a spontaneous phase transition.
- by a spontaneous phase transition.
Example: 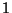 : high vessel (may have permeable wall) containing gas,
in a gravitational field.
: high vessel (may have permeable wall) containing gas,
in a gravitational field.
Example 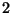 : Coffee subject to the potential of the mug, in
equilibrium with its smell.
: Coffee subject to the potential of the mug, in
equilibrium with its smell.
Example 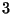 : Mixture (demixed) of two molecular species.
: Mixture (demixed) of two molecular species.
Examples
 :
:
- Fluids between walls
- Fluids in capillaries
- Fluid-solid phase transition
- Liquid crystals
- ...
Grand partition function, configurational:
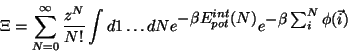 |
(1.2) |
where
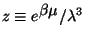 (
( de Broglie wave l.,
de Broglie wave l., 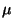
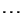 chemical potential
of the environment).
chemical potential
of the environment).
Grand potential:
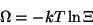 |
(1.3) |
 and
and 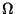 are functionals of
are functionals of 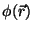 or
of the combination
or
of the combination
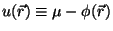 :
:
![\begin{displaymath}
\Xi = \Xi[u], \;\;\;\; \Omega = \Omega[u]
\end{displaymath}](img26.gif) |
(1.4) |


Next: 1.2 Functional Differentiation
Up: 1. Basics
Previous: 1. Basics
Franz J. Vesely Oct 2001
See also: "Computational Physics - An Introduction," Kluwer-Plenum 2001