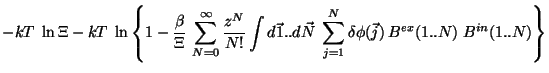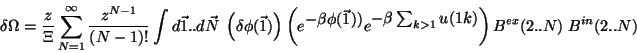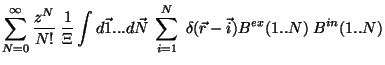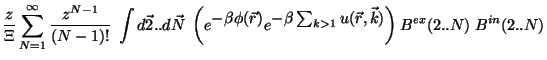

Next: Bibliography
Up: Density Functional Theory for
Previous: 4.3 Outlook
5. Appendix 1: Proof of
![$\rho_{eq}(\vec{r})=- \delta \Omega [u]/\delta u(\vec{r})$](img211.gif)
Grand Partition Function:
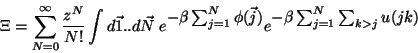 |
(5.1) |
Let us write the external and internal Boltzmann factors as
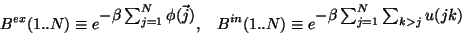 |
(5.2) |
Then
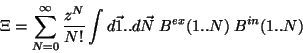 |
(5.3) |
Grand Potential:
![\begin{displaymath}
\Omega [\phi] \equiv -kT \; \ln \Xi
\end{displaymath}](img215.gif) |
(5.4) |
Varying the external potential according to 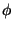
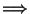
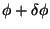 we find
we find
| |
|
![$\displaystyle \Omega [\phi+\delta \phi] =$](img219.gif) |
(5.5) |
| |
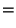 |
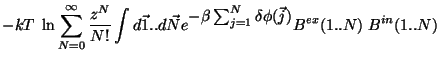 |
(5.6) |
| |
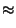 |
![$\displaystyle -kT \;\ln
\sum_{N=0}^{\infty} \frac{z^{N}}{N!}
\int d\vec{1}..d\v...
...[1-\beta \sum_{j=1}^{N}\delta \phi(\vec{j})\right]
B^{ex}(1..N) \; B^{in}(1..N)$](img222.gif) |
(5.7) |
| |
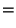 |
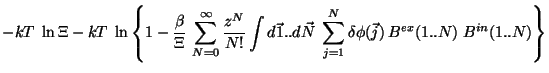 |
(5.8) |
| |
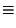 |
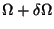 |
(5.9) |
It follows that
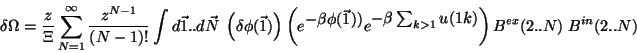 |
(5.10) |
On the other hand,
Therefore
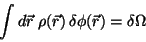 |
(5.12) |
Since
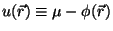 we have
we have
![\begin{displaymath}
\rho_{eq}(\vec{r})= - \frac{\delta \Omega [u]}{\delta u(\vec{r})}
\end{displaymath}](img28.gif) |
(5.13) |
q.e.d.
Back to text
 1.2
1.2


Next: Bibliography
Up: Density Functional Theory for
Previous: 4.3 Outlook
Franz J. Vesely Oct 2001
See also: "Computational Physics - An Introduction," Kluwer-Plenum 2001
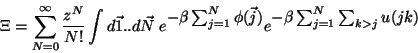
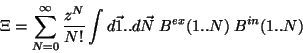
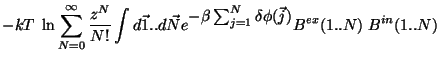
![$\displaystyle -kT \;\ln
\sum_{N=0}^{\infty} \frac{z^{N}}{N!}
\int d\vec{1}..d\v...
...[1-\beta \sum_{j=1}^{N}\delta \phi(\vec{j})\right]
B^{ex}(1..N) \; B^{in}(1..N)$](img222.gif)