


Next: 4. Application to Liquid
Up: 3. Approximations to
Previous: 3.2 Square Gradient Approximation
3.3 Weighted density Approximations (WDA)
LDA and SGA must fail if the local density can achieve high values.
For example, near a wall one may find density amplitudes in excess of
homogeneous dense packing.
In such cases it is best to smear out the density over a small spatial
region, using a suitable weighting function:
![\begin{displaymath}
{\rm\cal{F}}_{ex} [\rho ] =
\int d\vec{r} \rho(\vec{r}) \Psi_{ex}(\bar{\rho}(\vec{r}))
\end{displaymath}](img105.gif) |
(3.6) |
where
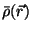 denotes the coarse-grained, or
smoothed, or weighted density.
denotes the coarse-grained, or
smoothed, or weighted density.
Various authors have contributed their specific recipes.
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_1.ps}
}$](img107.gif) Nordholm and Tarazona I:
Nordholm and Tarazona I:
For the excess free energy density NORDHOLM uses the
excluded volume approximation
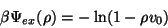 |
(3.10) |
where
 for hard spheres with diameter
for hard spheres with diameter  .
An improvement introduced by TARAZONA is the use of
the Carnahan-Starling approximation
.
An improvement introduced by TARAZONA is the use of
the Carnahan-Starling approximation
 |
(3.11) |
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_2.ps}
}$](img117.gif) Tarazona II:
Tarazona II:
where 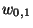 is taken from a virial expansion of
is taken from a virial expansion of
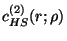 , and
, and 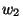 from a fit to the PY solution.
from a fit to the PY solution.
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_3.ps}
}$](img124.gif) Curtin-Ashcroft:
Curtin-Ashcroft:
Similar to Tarazona II but with more effort regarding 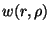 :
:
and 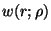 such that with
such that with
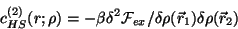 |
(3.17) |
it will produce the known pcf at all (homogeneous) densities.
Differenciating
![${\rm\cal {F}}_{ex}[\rho ]$](img1.gif) twice by the argument
twice by the argument
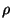 one obtains
one obtains
Various solution methods are possible. The standard procedure starts from
a Fourier transform of this equation:
![\begin{displaymath}
-\frac{1}{\beta} c_{k}^{(2)}(\rho)=
2 \Psi_{ex}'(\rho)w_{k}(\rho)
\left[ \Psi'_{ex}(\rho) w_{k}^{2}(\rho) \right]
\end{displaymath}](img131.gif) |
(3.19) |
For given
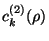 (e. g. from Percus-Yevick)
this equation may be solved numerically for
(e. g. from Percus-Yevick)
this equation may be solved numerically for 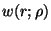 .
.
DENTON and ASHCROFT generalized this procedure
to mixtures.
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_4.ps}
}$](img133.gif) Meister-Kroll; Groot-v.d. Eerden:
Meister-Kroll; Groot-v.d. Eerden:
Let
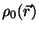 be a ``coarse-grained'', slowly
varying reference density. Expanding
be a ``coarse-grained'', slowly
varying reference density. Expanding
![${\rm\cal {F}}_{ex}[\rho ]$](img1.gif) around this reference density one finds
around this reference density one finds
with
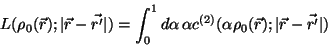 |
(3.22) |
and
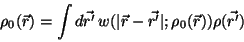 |
(3.23) |
 |
(3.24) |
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_5.ps}
}$](img141.gif) Percus; Robledo-Varea:
Percus; Robledo-Varea:
Starting from equ. 2.15 we write
![\begin{displaymath}
{\rm\cal{F}}_{ex} [\rho ] =
\int d\vec{r} \rho_{\sigma}(\vec{r}) \Psi_{ex}(\rho_{\tau}(\vec{r}))
\end{displaymath}](img142.gif) |
(3.25) |
where now 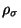 and
and 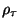 are suitably averaged
densities:
are suitably averaged
densities:
For the weighting functions 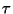 und
und  Robledo and
Varea suggest:
Robledo and
Varea suggest:
(Note that for the Tonks gas we have exactly
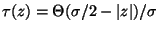 and
and
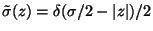 .)
.)
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_6.ps}
}$](img154.gif) Rosenfeld; Kierling-Rosinberg:
Rosenfeld; Kierling-Rosinberg:
Rosenfeld studied mixtures of hard spheres with radii  . We restrict
the discussion to one HS species, using the subsequently
introduced formulation of Kierling und Rosinberg.
. We restrict
the discussion to one HS species, using the subsequently
introduced formulation of Kierling und Rosinberg.
On the basis of geometric (overlap volume) consideration the following
representation may be derived:
![\begin{displaymath}
\beta {\rm\cal{F}}_{ex} [\{\rho(\vec{r})\} ]=
\int d\vec{r}\; \Phi(\{n_{\alpha}(\vec{r})\})
\end{displaymath}](img156.gif) |
(3.30) |
where 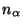 are several averaged densities:
are several averaged densities:
 |
(3.31) |
For the weighting functions
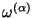 ,
,
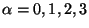 Kierlik-Rosinberg find
Kierlik-Rosinberg find
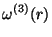 |
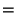 |
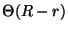 |
(3.32) |
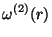 |
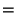 |
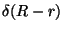 |
(3.33) |
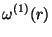 |
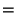 |
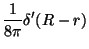 |
(3.34) |
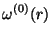 |
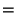 |
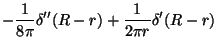 |
(3.35) |
The choice of the quantities 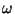 and the form of the function
and the form of the function
 follows from the requirement that in the homogeneous limit the
PY equation is fulfilled:
follows from the requirement that in the homogeneous limit the
PY equation is fulfilled:
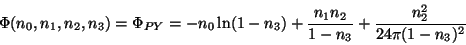 |
(3.36) |
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knots_jf.ps}
}$](img172.gif) WDA in Perspective:
WDA in Perspective:
The WDAs given above are mostly based on heuristic arguments.
For the ansatz of Meister-Kroll and Groot-v.d. Eerden
it was shown by Fischer et al. that it is equivalent to
the systematically derived Yvon-Born-Green approximation.
![$\textstyle \parbox{210pt}{
\includegraphics[width=180pt]{images/fischer_sok.ps}
}$](img173.gif)
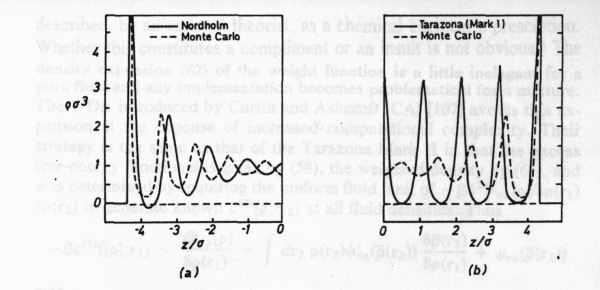
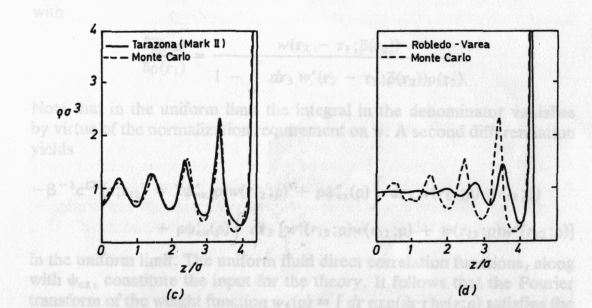
The application of various WDAs to the sample problem of hard spheres
between two walls the following picrure emerges (from Evans 92):
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_7.ps}
}$](img174.gif) Modified WDA:
Modified WDA:
Denton and Ashcroft suggested to apply a second averaging process
to the ``weighted density''
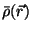 , this time averaging
over the entire system. The resulting density
, this time averaging
over the entire system. The resulting density
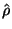 is then inserted in an expression for
is then inserted in an expression for
![${\rm\cal {F}}_{ex}[\rho ]$](img1.gif) :
:
![\begin{displaymath}
\frac{{\rm\cal{F}}_{ex} [\rho ]}{N} = \Psi_{ex}(\hat{\rho})
\end{displaymath}](img176.gif) |
(3.37) |
with
 |
(3.38) |
The function  is chosen such that the above equations
reproduce the correct direct pcf
is chosen such that the above equations
reproduce the correct direct pcf
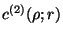 :
:
![\begin{displaymath}
\hat{w}(r;\rho)=-\frac{1}{2\Psi_{ex}'(\rho)}
\left[ kT \;c^{(2)}(\rho;r)+\frac{1}{V}\rho \Psi_{ex}''(\rho)\right]
\end{displaymath}](img180.gif) |
(3.39) |
If one uses the direct pcf and the free energy density 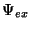 according to Percus-Yevick the fluid-solid phase transition of
hard spheres is well reproduced. Also, the enhomogeneous fluid density
near a wall is well represented.
according to Percus-Yevick the fluid-solid phase transition of
hard spheres is well reproduced. Also, the enhomogeneous fluid density
near a wall is well represented.
A similar ansatz is due to Lutsko and Baus. Their
``Generalized Effective Liquid Approximation'' (GELA)
produces useful results at the freezing transition.



Next: 4. Application to Liquid
Up: 3. Approximations to
Previous: 3.2 Square Gradient Approximation
Franz J. Vesely Oct 2001
See also: "Computational Physics - An Introduction," Kluwer-Plenum 2001
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_1.ps}
}$](img107.gif) Nordholm and Tarazona I:
Nordholm and Tarazona I:
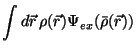
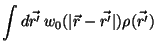
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_2.ps}
}$](img117.gif) Tarazona II:
Tarazona II:
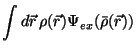
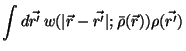
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_3.ps}
}$](img124.gif) Curtin-Ashcroft:
Curtin-Ashcroft:
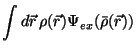
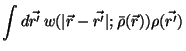
![]() twice by the argument
twice by the argument
![]() one obtains
one obtains

![$\displaystyle \rho \Psi_{ex}'(\rho) \int d\vec{3}
\left[ w'(13;\rho)w(32;\rho)+w(13;\rho)w'(32;\rho) \right]$](img130.gif)
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_4.ps}
}$](img133.gif) Meister-Kroll; Groot-v.d. Eerden:
Meister-Kroll; Groot-v.d. Eerden:
![]() be a ``coarse-grained'', slowly
varying reference density. Expanding
be a ``coarse-grained'', slowly
varying reference density. Expanding
![]() around this reference density one finds
around this reference density one finds
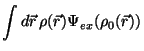
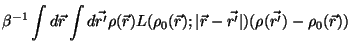
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_5.ps}
}$](img141.gif) Percus; Robledo-Varea:
Percus; Robledo-Varea:

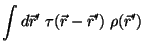
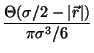
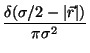
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_6.ps}
}$](img154.gif) Rosenfeld; Kierling-Rosinberg:
Rosenfeld; Kierling-Rosinberg:
![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knots_jf.ps}
}$](img172.gif) WDA in Perspective:
WDA in Perspective:
![$\textstyle \parbox{210pt}{
\includegraphics[width=180pt]{images/fischer_sok.ps}
}$](img173.gif)

![$\textstyle \parbox{60pt}{
\includegraphics[width=54pt]{images/knot_7.ps}
}$](img174.gif) Modified WDA:
Modified WDA: