1.3.2 Second Derivatives

The same procedure as before yields

DDNGF:

$${F_{k}}'' \approx \frac{1}{(\Delta x)^{2}} \left[ \Delta^{2} \mbox{$f_{k}$} - \Delta^{3} \mbox{$f_{k}$}+ \frac{11}{12} \Delta^{4} \mbox{$f_{k}$}- \dots \right]$$

Example:

$${F_{k}}'' = \frac{1}{(\Delta x)^{2}} \Delta^{2} \mbox{$f_{k}$}+ O(\Delta x)$$

$$= \frac{1}{(\Delta x)^{2}} \left[ f_{k+2}-2f_{k+1}+f_{k}\right] + O(\Delta x)$$

$$\;\;{\rm\hspace{12em}(pretty \hspace{0.6 ex} bad!)}$$

Let's try again....

DDNGB:

$${F_{k}}'' \approx \frac{1}{(\Delta x)^{2}} \left[ \nabla^{2} \mbox{$f_{k}$} + \nabla^{3} \mbox{$f_{k}$}+ \frac{11}{12} \nabla^{4} \mbox{$f_{k}$}+ \dots \right]$$

Example:

$${F_{k}}'' = \frac{1}{(\Delta x)^{2}} \nabla^{2} \mbox{$f_{k}$}+ O(\Delta x)$$

$$= \frac{1}{(\Delta x)^{2}} \left[ f_{k}-2f_{k-1}+f_{k-2}\right] + O(\Delta x)$$

$$\;\;{\rm\hspace{10em}(pretty \hspace{0.6 ex} bad,\hspace{0.6 ex} too!)}$$

And the winner is...

DDST:

$${F_{k}}'' \approx \frac{1}{(\Delta x)^{2}} \left[ \delta^{2} \mbox{$f_{k}$}- \frac{... ...elta^{4} \mbox{$f_{k}$} + \frac{1}{90} \delta^{6} \mbox{$f_{k}$}- \dots \right]$$

Example:

$${F_{k}}'' = \frac{1}{(\Delta x)^{2}} \delta^{2} \mbox{$f_{k}$} + O\left[(\Delta x)^{2}\right]$$

$$= \frac{1}{(\Delta x)^{2}} \left[ f_{k+1}-2f_{k}+f_{k-1}\right] + O\left[(\Delta x)^{2}\right]$$

$$\;\;{\rm\hspace{12em}(much \hspace{0.6 ex} better!)}$$

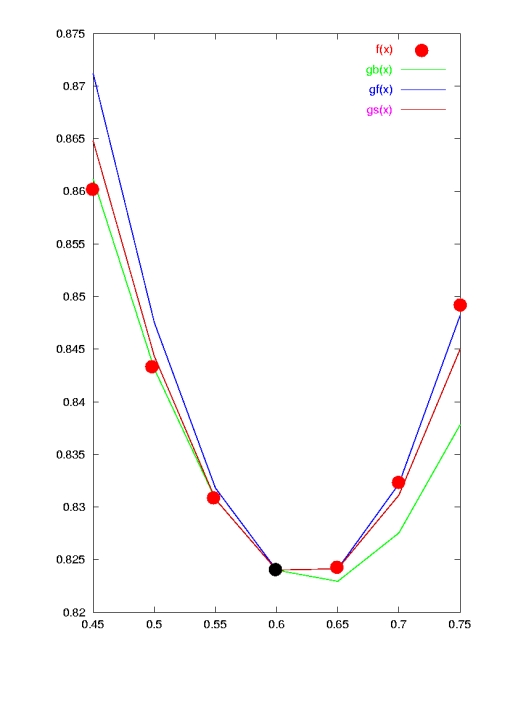
Figure: Interpolation, including first and second derivatives as approximated by backward (blue), forward (green) and Stirling (red) differencing. In the neighborhood of $x_{k}$ (black dot) the tabulated function is best represented by Stirling. The interpolation curves are actually parabolas, but as only their values at $x_{k \pm l}$ are of interest they are drawn as broken lines.