
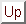

Truncated ellipsoid capped by sphere segments with continuous
tangents
Advantages:
- (a) convex everywhere
- (b) smectic phase in pure fluid
- (c) shape may be tuned between spherocylinder and ellipsoid
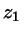 ... truncation half length (given)
... truncation half length (given)
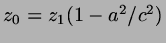 ... center of cap
... center of cap
![$r_{c}^{2}=a^{2}[1-(z_{1}^{2}/c^{2})(1-a^{2}/c^{2})]$](img72.png) ... radius of cap
... radius of cap
Excluded volume SE-SP:
Truncation half length
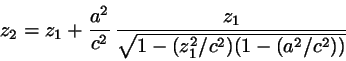 |
(8) |
 Chebysheff polynomials for body:
Chebysheff polynomials for body:
with 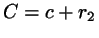 ,
, 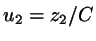 , and
, and
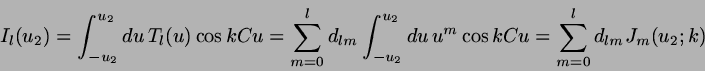 |
(10) |
The integrals 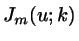 obey the recursion
obey the recursion
To this we add the caps according to
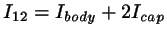 . The cap parameters are
. The cap parameters are
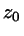 (center),
(center), 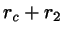 (radius), and
(radius), and
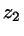 (rim).
(rim).
(No MC results yet)

 F. J. Vesely / University of Vienna
F. J. Vesely / University of Vienna
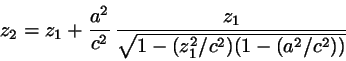
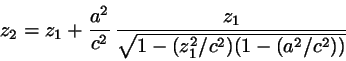
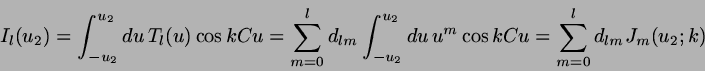
 Applet Koda_se:
Start
Applet Koda_se:
Start