Again, let ![]() denote the short and long (
denote the short and long (![]() -) semiaxes of an ellipse.
Truncate the ellipse at some distance
-) semiaxes of an ellipse.
Truncate the ellipse at some distance ![]() from its center and complete
the figure by circle segments having the same tangent as the ellipse at the
point of fusion. Rotate the figure around the long axis to produce a
spheroellipsoid. The pertinent equations are:
from its center and complete
the figure by circle segments having the same tangent as the ellipse at the
point of fusion. Rotate the figure around the long axis to produce a
spheroellipsoid. The pertinent equations are:
![]() (center of circle segment);
(center of circle segment);
![]() (radius of circle segment). The volume of a spheroellipsoid is
(radius of circle segment). The volume of a spheroellipsoid is
![]() , where
, where
![]() and
and
![]()
Applying Koda's theory to a mixture of hard spheroellipsoids (SE) and spheres
(SP) with the same diameter we make use of the relations derived earlier.
For the encounter SE-SE between two parallel spheroellipsoids we find
that the excluded volume is again a spheroellipsoid with the following
parameters: axes ![]() ,
, ![]() ; truncation half-length
; truncation half-length ![]() ,
center
,
center ![]() and radius
and radius ![]() of cap are all double the values
pertaining to the individual particles.
The cosine integral
of cap are all double the values
pertaining to the individual particles.
The cosine integral ![]() is then made up of a part referring to the
truncated ellipsoidal body and to the spherical caps:
is then made up of a part referring to the
truncated ellipsoidal body and to the spherical caps:
![]() , where
, where
![$\displaystyle 12 \frac{C}{A} \frac{1}{kC}
\left[
\left( 1+\frac{2}{(kC)^{2}}-\f...
...2}}{(kC)^{2}} \right) \sin kz_{1}
-\frac{2kz_{1}}{(kC)^{2}} \cos kz_{1}
\right]$](img154.png) |
(34) |
In the case of the SE-SP contact the truncated body of the excluded
volume is again the high-order oval which we encountered before.
The truncation half-length is now given by
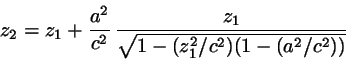 |
(35) |
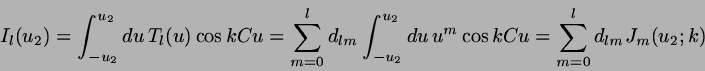 |
(37) |