Quantentheorie
Unterrichtskonzept - ein ungewöhnlicher Einstieg
Neuere Experimente auf dem Gebiet der Grundlagen der Quantentheorie, die zum Teil erhebliche Medienpräsenz erlangen, lassen eine Revision des "klassischen" Quantentheorie-Unterrichts, die Hinzunahme neuer Gesichtspunkte und die Verschiebung von Prioritäten wünschenswert erscheinen. Dies umso mehr, als österreichische Forscher an führender Front an den jüngsten Entwicklungen beteiligt sind.
Im Folgenden wird ein Konzept vorgestellt, wie eine zeitgemäße Einführung in die Quantentheorie aussehen könnte. Die ersten 7 Kapitel sind in Form eines Textes, der die Darstellung der relevanten Inhalte zusammenfaßt und sich sprachlich an SchülerInnen richtet, ausformuliert worden. Der Einstieg erfolgt im Wesentlichen über das Licht und das Verhalten einzelner Photonen. Eine einfache Versuchsanordnung (Mach-Zehnder-Interferometer) erlaubt erstaunlich tiefgehende Einsichten. Ohne weitere Vorbereitung kann dann anhand des Elitzur-Vaidmann-Bombentest-Experiments darauf eingegangen werden, daß die Begriffe Information, Kausalität und Lokalität in Quantensystemen in unerwarteter Weise problematisch werden. Dieser Zugang erlaubt es, viel tiefer - und bis zum Begriff der Quanteninformation praktisch ohne Rechnung! - in die eigentliche Natur von Quantenphänomenen einzudringen und auf die in der modernen Forschung geführten Debatten einzugehen, als dies im traditionellen Quantentheorie-Unterricht der Fall ist.
Die weiteren Kapitel 8 - 18, aus denen im konkreten Unterricht in Anbetracht der Vielfalt eine Auswahl getroffen werden muß, liegen - mit Ausnahmen von Kapitel 17 - nur skizzenhaft vor. Insbesondere Kapitel 14 steht mit der für den Einstieg gewählten Interferometer-Anordnung in engem Zusammenhang, sodaß eine geeignete didaktische Aufbereitung der modernen Themen Quantencomputer und Quanten-Teleportation auf der Basis des hier dargestellten Zugangs nicht (mehr) außer Reichweite liegt. In Kapitel 18 wird noch auf die Frage, ob die Begriffe des Beobachters und der Messung nicht einer einheitlichen quantentheoretischen Naturauffassung entgegenstehen, eingegangen. Auch hier wird auf das am Anfang stehende Interferometer-Experiment zurückgrgriffen.
"Licht ist eine Welle". Das ist im Wesentlichen der Standpunkt des 19.
Jahrhunderts. Er ist voll ausformuliert in den "Maxwellschen Gleichungen",
die zu den wichtigsten Meilensteinen der klassischen Physik gehören.
Was "schwingt" bei einer elektromagnetischen Welle? Die beiden fundamentalen
Felder dieser Theorie (das elektrische und das magnetische), die ihre physikalische
Natur direkt durch ihre Wirkungen auf Ladungen offenbaren. In einer ebenen
Welle stehen diese beiden Felder normal zur Ausbreitungsrichtung (und das
elektrische normal zum magnetischen). Das führt zum Begriff der Polarisation
(die bei der prinzipiellen Diskussion von Wellenvorgängen oft vernachlässigt
werden kann).
Zwei auf einen Schirm fallende Lichtwellen können interferieren
(d.h einander überlagern), weil ihre Felder einfach addiert
werden. Zeigt etwa in einem Punkt des Raums das elektrische Feld der einen
Teilwelle nach oben, das der anderen nach unten, und haben beide denselben
Betrag, so ist das resultierende elektrische Feld in diesem Raumpunkt Null.
Trifft dasselbe auch für die magnetischen Felder zu (etwa: eines zeigt
nach rechts, eines nach links), so findet in diesem Punkt vollständige
Auslöschung ("destruktive Interferenz") statt. Analog
können zwei Teilwellen einander maximal verstärken ("konstruktive
Interferenz"). Wird die Polarisation außer acht gelassen, so
herrschen ähnliche Verhältnisse wie für Oberflächenwellen
einer Flüssigkeit (Wellenwanne).
2. Licht besteht aus Teilchen, den Photonen
"Licht besteht auf Photonen". Das ist der Standpunkt, der zu Beginnn des 20. Jahrhunderts (vor allem von Max Planck und Albert Einstein) entwickelt wurde. Belichtet man einen Film bei sehr geringer Intensität, so besteht das Bild aus einzelnen belichteten Punkten, nicht aus einer kontinuierlichen Helligkeitsverteilung. Das Licht besteht also offenbar aus Teilchen. Man nennt sie Photonen oder Lichtquanten. Heute ist es technisch möglich, einzelne Photonen zu erzeugen.
Die Bezeichnung Teilchen ist wörtlich zu nehmen: Wann immer
versucht wird, den Ort eines Photons zu messen - also, indem man ihm einen
photographischen Film oder Ähnliches in den Weg stellt - , so trifft
es irgendwo auf dieser Fläche auf. Diese Eigenschaft von Licht ist
in Beschleunigeranlagen untermauert worden. Bis heute gibt es keinen experimentellen
Hinweise daraus, daß ein Photon eine innere Struktur hat, daß
es also nicht als "Punkt" beschrieben werden könnte. In diesem Zusammenhang
tritt eine neue Naturkonstante auf - das Plancksche Wirkungsquantum
h : Licht der Frequenz f besteht aus Photonen der
Energie E = h f . (Wir benötigen diese Beziehung fürs erste
nicht und werden später darauf zu sprechen kommen).
Dabei ist aber die Vorstellung, bei einem Photon handle es sich um eine
ausgedehnte Welle dieser Freuqenz (und der entsprechenden Wellenlänge
l = c/f ) innerhalb eines kleinen Raumgebiets
(ein "Wellenpaket"), definitiv falsch. (Denn dann müßte ein
auf einen Schirm fallendes Photon einen ausgedehnten Fleck bewirken, was
nach dem gegenwärtigen Stand unseres experimentellen Könnens
nicht beobachtet wird).
Um Mißverständnissen vorzubeugen:
Das Photon ist ein Teilchen, und es tritt nie anders auf. Noch niemand
hat ein "wellenförmiges Photon" gesehen. Eines der unglückseligsten
Mißverständnisse über die Quantentheorie ist der "Dualismus
von Welle und Teilchen". Dieses Schlagwort verdeckt, was es eigentlich
ursprünglich erhellen sollte, und wird am besten gar nicht verwendet.
3. Was interferiert?
Damit besteht aber ein Dilemma: wie kommen die für Licht in zahllosen Situationen beobachteten Interferenzerscheinungen zustande? Eine dunkle Stelle in einem Interferenzbild bedeutet, daß nur wenige Photonen dort aufgetroffen sind, eine helle Stelle bedeutet, daß viele Photonen dort aufgetroffen sind. Eine einfache Versuchsanordnung verdeutlicht das Problem:

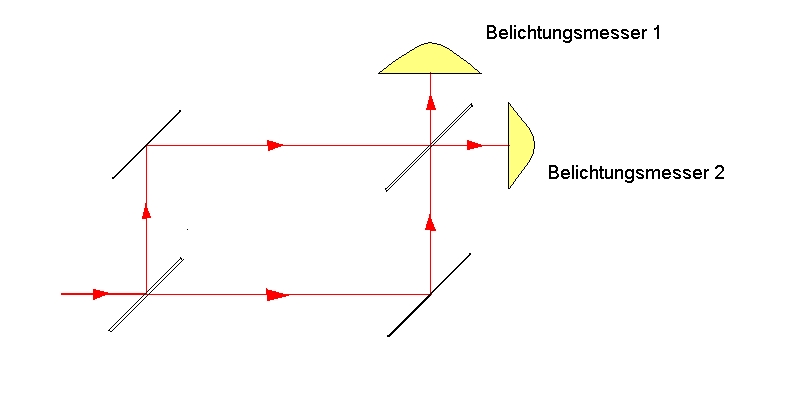
Ein Lichtstrahl wird (durch einen halbdurchlässigen Spiegel) in zwei Teilstrahlen aufgespalten und wieder (mit Hilfe zweier normaler und eines weiteren halbdurchlässigen Spieles) zusammengeführt. Die in die Belichtungsmesser fallenden Strahlen bestehen jeweils aus zwei zusammengeführten Teilstrahlen. Soweit, so gut.
Nun ist das Diagramm 1 nicht ganz richtig gezeichnet. Es suggeriert,
die beiden Belichtungsmesser würden jeweils Licht gleicher Intensität
empfangen. Eine einfache Überlegung zeigt, daß das nicht
der Fall ist: Für die beiden in den Belichtungsmesser 2 fallenden
Teistrahlen herrschen jeweils identische Bedingungen. Beide (jener, der
den oberen Weg und jener, der den unteren Weg genommen hat) sind einmal
"nach links" und danach "nach rechts" reflektiert worden. Nach Durchtritt
des zweiten halbdurchlässigen Spiegels sind sie in Phase. Sie interferieren
konstruktiv, d.h. sie addieren einander, so als ob sie nie getrennt worden
wären. Belichtungsmesser 2 empfängt also Licht derselben Intensität
wie sie der in die Apparatur einfallende Strahl hatte. Daher bleibt für
Belichtungsmesser 1 nichts mehr übrig, denn die gesamte Intensität
kann sich nicht vergrößert haben. Die beiden in Belichtungsmesser
1 fallenden Strahlen müssen einander also auslöschen! Diese
auf den ersten Blick seltsame Erscheinung kann durch eine detaillierte
Betrachtung der beiden in Belichtungsmesser 1 fallenden Teilstrahlen überprüft
werden: für sie herrschen nicht die gleichen Verhältnisse,
denn sie haben jeweils eine vom anderen verschiedene "Geschichte". Jener
Teilstrahl, der den unteren Weg genommen hat, ist nur einmal reflektiert
worden, während jener, der den oberen Weg genommen hat, insgesamt
dreimal reflektiert worden ist.
Jede Reflexion an einem der halbdurchlässigen
Spiegeln bewirkt nun einen Phasensprung
von l/4 (als Netto-Effekt der Überlagerung
mehrerer durch innere Reflexion zustandegekommender Teilstrahlen).
Der Phasensprung an einem "echten" Spiegel ist l/2.
Der untere Teilstrahl hat also entlang
seines Wegs einen Phasensprung von l/2 erhalten,
während sich die drei Reflexionen des oberen Teilstrahls als Netto-Phasensprung
von l/4 + l/2 + l/4
= l auswirken. Insgesamt haben die beiden
Teilstrahlen damit eine Phasendifferenz von l/2 zueinander,
was Auslöschung bewirkt!
[An dieser Stelle mein Dank an Jörg Schulenburg,
der durch eine kritische Frage half, einen Fehler in meiner Argumentation auszubügeln
- Jan 2001].
Quellen hierzu:
- Das Buch Shadows of the Mind von Roger Penrose (Vintage 1995), Fußnote Nr. 7 auf Seite 305.
- Diskussion des Mach-Zehnder-Interferometers
(Projekt qubit - Quanteninformation in der Schule)
Mit einem Wort: In den Belichtungsmesser 1 fällt überhaupt kein Licht, während Belichtungsmesser 2 die Intensität des einfallenden Strahls mißt. (Eine derartige Anordnung wird als Mach-Zehnder-Interferometer bezeichnet. Sie wird in der Praxis etwa dazu benützt, um kleinste Dichteunterschiede in Medien zu messen. Dazu bringt man das zu untersuchende Medium in einen der beiden Strahlengänge, wodurch die Symmetrie, die für die beiden in den Belichtungsmesser 2 fallenden Teilstrahlen zerstört wird. Die daraus folgende Veränderung der gemessenen Licht-Intensitäten gibt Aufschluß über die Eigenschaften des Mediums).
Das Diagramm, das unsere Versuchsanordnung schematisch darstellt, müßte also eigentlich so gezeichnet werden:

Die Situation ist stark idealisiert, und mehrere Dinge wurden der Einfachheit halber vernachlässigt:
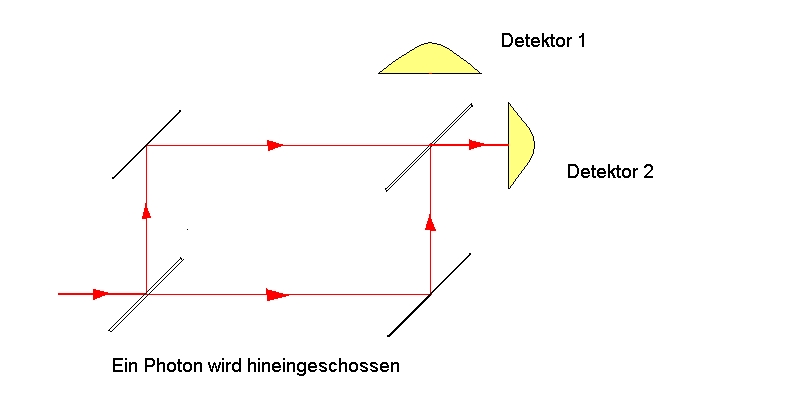
Das experimentelle Ergebnis ist eindeutig: auch ein einzelnes Photon
trifft immer auf den Detektor 2. Die zahlreichen Photonen, aus denen
ein heller Lichtstrahl besteht, tun also offensichtlich unabhängig
voneinander alle dasselbe. Umso rätselhafter ist also das Ausbleiben
von Photonen, die der Detektor 1 registrieren würde. Woher "weiß"
ein einzelnes Teilchen, daß es den Weg in den Detektor 1 nicht nehmen
kann? Um noch mehr über das Verhalten der Photonen herauszufinden,
kann die Anordnung ein bißchen aus dem Lot gebracht werden, etwa
so:
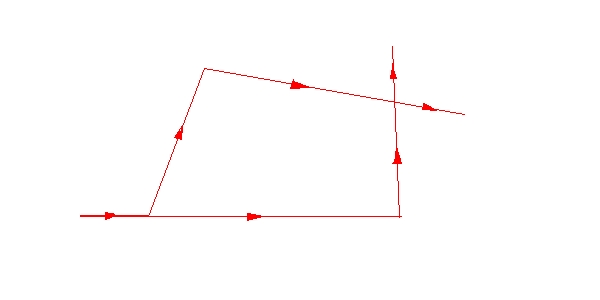
Die Spiegeln können nachträglich immer richtig positioniert werden. Die Auslöschung im Belichtungsmesser 1 wird dadurch gestört. Man könnte die Strahlengänge etwa so einstellen, daß die von beiden Belichtungsmessern erfahrenen Lichtintensitäten im Verhältnis 70 : 30 stehen. Schießt man wieder einzelne Photonen in die Apparatur, so wird jedes Photon immer nur von einem der beiden Detektoren registriert werden. Wird das Experiment oft wiederholt, so wird die Zahl der Detektorklicks im Verhältnis 70 : 30 stehen. Wenn nun aber die einzelnen Photonen voneinander unabhängig sind, so läßt dies Vermutung zu, beim Verhältnis 70 : 30 handelt es sich um Wahrscheinlichkeiten für ein einzelnes Photon, auf einen der beiden Detektoren zu treffen. Ist die "Lichtwelle" eine bloße Wahrscheinlichkeit für das Tun und Lassen einzelner Photonen? Und heißt das, daß sich einzelne Photonen nicht streng deterministisch verhalten, d.h. daß das zukünftige Verhalten eines gegebenen Photons nicht exakt vorausgesagt werden kann?
Die hier behandelte einfache experimentelle Interferometer-Anordnung ist nur ein Spezialfall einer allgemeineren Eigenschaft von Teilchen. In modernen Experimenten der Atom- und Teilchenphysik stößt man immer wieder auf ähnliche Situationen, so daß es sich um eine Frage von fundamentaler Bedeutung für unser Wissen über die Natur handelt.
4. Das Zusammenspiel von Welle und Teilchen
Fragen wir nicht nach dem "Warum", sondern nach dem "Wie", so läßt sich das Verhalten der Photonen in folgender Weise beschreiben:
Postulat (Quantentheorie des Lichts):
Diese Möglichkeitswelle hat also nicht den Status einer physikalischen Meßgröße, sondern eher den einer mathematischen Hilfsgröße. Sie kommt durch den konkreten Aufbau eines Experiments zustande, kann also vor der Beobachtung ermittelt werden. Im Fall des Zusammentreffens von Teilwellen tritt Interferenz (Überlagerung) auf. Die Ermittlung der Möglichkeitswelle ist also ein theoretische Angelegenheit. Ist die Welle bekannt, so kann sie für statistische Vorhersagen verwendet werden. Erst wenn eine sehr große Anzahl von Photonen im Spiel ist, entsteht der Eindruck eines Wellenverhaltens, wie es aus der Physik der elektromagnetischen Erscheinungen bekannt ist. Insofern behält der Begriff der Lichtwelle seine Bedeutung als Näherung für den Fall großer Photonenzahlen.
Ein einzelnes Photon verhält sich hingegen so, als ob es den Verlauf der Welle kennen würde und sich dadurch über die Wahrscheinlichkeiten seiner vorhandenen Möglichkeiten orientiert. Wenn das tatsächlich zutrifft, dann läßt sich keine definitive Vorhersage über das Verhalten einzelner Photonen treffen, sondern nur eine Wahrscheinlichkeitsaussage (außer im Fall, daß die Welle nur einer einzigen Möglichkeit die Wahrscheinlichkeit 1 ergibt und allen anderen die Wahrscheinlichkeit 0, wie es z.B. im Diagramm 2 der Fall ist).
Von einem System, in dem (Möglichkeits-)Welle und (beobachtetes) Teilchen auf eine solche Weise zusammenspielen, sagen wir, daß es sich in einem bestimmten Quantenzustand befindet. Ein Quantenzustand ist also in erster Linie durch seine Möglichkeitswelle bestimmt.
Es wurde viel Anstrengung darauf verwendet, Auswege zu suchen, die Vorgänge wie den oben besprochenen Interferometerversuch in streng deterministischen Modellen zu beschreiben.
Diskussion: Wie kann man das Verhalten der Photonen sonst noch erklären?
Sie sind im Großen und Ganzen fehlgeschlagen. Die Quantentheorie
hat die größte Umwälzung der Physik in ihrer Geschichte
gebracht, und sie ist wohl auch (vielleicht zusammen mit der Relativitätstheorie)
die erfolgreichste aller physikalischen Theorien. Wir werden im Folgenden
einige ihrer Züge - in vereinfachten Situationen wie der obigen Interferometer-Versuchsanordnung
- besprechen.
5. Unbestimmtheit
Die bisher gewonnene Theorie hat weitreichende Konsequenzen. Kehren wir zurück zu dem in Diagramm 2 dargestellten Experiment. In der klassischen Physik findet zwischen den beiden auf den Belichtungsmesser 1 zulaufenden Teilwellen Auslöschung statt. An die Stelle des klassischen Feldes tritt nun die Möglichkeitswelle, und wir konstruieren sie genauso, wie zuvor die Lichtwelle ermittelt wurde. Insbesondere besitzt sie dieselbe Wellenlänge, sodaß die auf den Detektor 1 zulaufenden Teilwellen einander auslöschen (und die auf den Detektor 2 zulaufenden Teilwellen einander maximal verstärken). Die roten Linien in den Diagrammen symbolisieren also in der klassischen Physik die Lichtwelle, in der Quantentheorie die Möglichkeitswelle. Da nun in Summe keine Welle im Detektor 1 ankommt, ist auch die Wahrscheinlichkeit für ein einzelnes Photon, dort registriert zu werden, Null. Die Voraussage lautet daher: "Alle Photonen werden von Detektor 2 registriert" - in Übereinstimmung mit dem experimentellen Beobachtungsresultat.
"Quantensysteme" verhalten sich seltsam. Woher "kennt" das Photon das Verhalten der Wahrscheinlichkeitswelle? Woher "weiß" es, daß beim Detektor 1 die Auslöschung zweier Teilwellen statffindet? Wenn es nur einen der beiden möglichen Wege (den oberen oder den unteren) genommen hat, woher "weiß" es, daß der andere auch möglich gewesen wäre (daß also dort kein Hindernis im Weg steht)? Nur dieses Möglich-Sein des anderen Weges erlaubt es den Möglichkeits-Teilwellen, einander auszulöschen. Ist etwa im oberen Strahlengang ein Hindernis, so hat auch der Strahlengang einen anderen Verlauf:
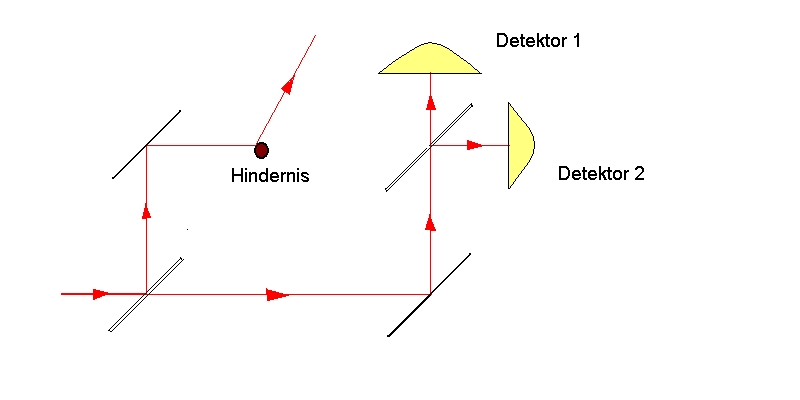
Ein Hindernis zerstört also die Auslöschung, sodaß nun beide Detektoren (mit gleicher Wahrscheinlichkeit) das Photon registrieren können. Daher kann es nicht sein, daß ein Photon einfach den unteren Weg nimmt und sich um sonst nichts kümmert! Und genauso ist es mit dem oberen Weg, denn es könnte ja der untere versperrt sein. Es ist so, also ob das Photon beide Wege genommen hätte! Kann man die Frage experimentell entscheiden?
Diskussion über diese Frage.
Die Antwort lautet "nein", denn jeder weitere Detektor in einem Strahlengang,
der versucht, den eingeschlagenen Weg herauszufinden, stört die Auslöschung
der Teilwellen beim Detektor 1 und entspricht eher einem Hindernis wie
im Diagramm 4. Auf eine unseren Anschauungen schwer begreifliche Weise
hängen die Detektorklicks von den Verhältnissen auf beiden
Wegstrecken ab. Ist ein Weg versperrt, so können beide Detektoren
das Photon (mit gleicher Wahrscheinlichkeit) registrieren, sind beide Wege
offen, so wird es immer im Detektor 2 ankommen! In diesem letzten Fall
scheint dem von einem einzelnen Photon eingeschlagenen Weg also gar keine
"objektive Realität" zuzukommen. Nicht nur ist er uns prinzipiell
verborgen - d.h. der Messung unzugänglich -, es scheint ihn gar
nicht "zu geben"! Man spricht dabei von einer quantentheoretischen Unbestimmtheit.
Neuere Experimente haben die Vermutung untermauert, daß derartigen
Alternativen (oberer Weg - unterer Weg) tatsächlich keine "objektive
Realität" zukommt, d.h. daß es sich dabei nicht bloß um
Unkenntnis handelt, sondern um ein echtes Nicht-Festgelegt-Sein! Dafür
gibt es sogar ein eigenes Wort: ein Photon nimmt virtuell beide
Wege. Ein virtueller Prozeß ist einer, in den man nicht durch Messung
eingreifen kann, ohne ihn zu zerstören, über den man also durch
Beobachtung nichts erfahren kann. Man sagt auch manchmal, der Zustand des
Systems ist eine Superposition (was soviel heißt wie "Überlagerung")
der beiden Möglichkeiten "das Photon nimmt den oberen Weg" und "das
Photon nimmt den unteren Weg".
Mathematisch gesehen ist die Wellenfunktion des
Photons vor dem Auftreffen auf den zweiten halbdurchlässigen Spiegel
y(gesamt) = y(oberer
Weg) + y(unterer Weg). Das Wort Superposition
bezieht sich auf die Möglichkeit, Wellenfunktionen zu addieren.
Wir müssen die Frage, welchen Weg ein bereits registriertes Photon genommen hat, auf diese seltsame Weise offenlassen!
Man kann übrigens an dieser Stelle bereits erkennen, warum die
Quantentheorie vor allem im Mikrokosmos bedeutsam ist und sich in
unserer makroskopischen Alltagswelt nicht auf Anhieb zeigt: Um eine experimentelle
Interferometer-Anordnung wie die oben besprochene tatsächlich zu realisieren,
müssen die beiden Lichtwege extrem gut gegenüber äußeren
Einflüssen abgeschirmt werden. Selbst ein einziges zusätzliches
Photon, das einen Strahlengang kreuzt, kann als Hindernis auftreten eine
der beiden Teilwellen unterbrechen. Nun ist unsere Welt aber von Photonen
übersät: jeder Körper einer bestimmten Temperatur emittiert
elektromagnetische Wärmestrahlung - also Photonen! Diese würden
auf die Versuchsanordnung wie das Hindernis im Diagramm 4 wirken und die
Interferenz der Teilwellen unterdrücken. Die unvermeidliche Wechselwirkung
mit der Umgebung, und seien es nur die Photonen der Wärmestrahlung,
wird heute von den meisten Quantentheoretikern als der Grund dafür
angesehen, daß sich Quantenphänomene nicht (oder nur selten)
an makroskopischen Objekten zeigen, warum unsere Alltagswelt also "klassisch"
erscheint, obwohl die Natur insgesamt mit Hilfe einer Quantentheorie
beschrieben wird. Interferenzerscheinungen können hingegen in sehr
kleinen Raumgebieten, etwa innerhalb von Atomen, ungestört stattfinden.
Im Allgemeinen ist es nur unter erheblichem Aufwand und versierter Experimentierkunst
möglich, Quantenzustände, wie jenen in unserer Versuchsanordnung,
über makroskopische Distanzen aufrechtzuerhalten. (Ausnahmen sind
die sogenannten "makroskopischen Quantenzustände", von denen die bekanntesten
die Supraleitung, die Superfluidität und der Laser sind).
6. Denken und Sprechen über die Quantentheorie
Die hier besprochene Situation stellt auch PhysikerInnen immer wieder vor das Problem, wie am besten über die Quantenwelt nachgedacht und gesprochen werden soll. Unsere althergebrachte Art des Schließens und Argumentierens wird auf eine harte Probe gestellt. Wie wir an der Unbestimmtheit des von den einzelnen Photonen eingeschlagenen Weges sehen können, erhalten die Begriffe "und " und "oder" eine neue Bedeutung. Einander (nach klassischem Verständnis) ausschließende Alternativen können auf "virtuelle" Weise beide zu einer Beobachtung "beitragen". Dennoch bedeutet die Quantentheorie nicht das Ende jeglicher Logik. Sie will ja schließlich Bestandteil der Physik sein, und gewisse Grundzüge aller physikalischer Theorien (vor allem das Erstellen überprüfbarer Vorhersagen) bleibt auch hier gültig.
Die Quantentheorie steht im Ruf, einen hochgezüchteten mathematischen Apparat zu benützen, der Nicht-Eingeweihten kaum zugänglich ist. Das stimmt zwar, aber dieser Apparat dient vor allem dazu, Wahrscheinlichkeiten für mögliche Beobachtungsresultate zu berechnen. In der einfachen Situation, die wir bisher diskutiert haben (ein Photon im Interferometer) sind die auftretenden Wahrscheinlichkeiten aber bereits im voraus eingestellt worden - durch die Auslöschung der Teilwellen bei Detekor 2. Es gibt also hier nichts weiter zu rechnen, und so können alle, die das Problem ernstnehmen, darüber nachdenken und diskutieren.
Spezialisten haben verschiedene Auswege aus dieser Situation entwickelt. Die beiden Extrempositionen sind:
7. Quanteninformation
Wir haben die Skala an seltsamem Verhalten von Quantensystemen noch nicht ganz ausgelotet. Man könnte sich damit zufriedengeben, daß gewisse Dinge, die vor einer Messung passiert sind (z.B. der von einem Photon genommene Weg) prinzipiell unbestimmt sind, und daß die darauf gerichteten Fragen nicht gestellt werden. Damit verzichtet man aber auf den Genuß weiterer faszinierender, exotisch anmutender Eigenschaften der Mikrowelt. So werden grundlegende Begriffe der klassischen Physik wie Kausalität und Lokalität durch sie erschüttert. Es ist nicht schwer, das einzusehen. Wir können dazu die oben besprochene Apparatur verwenden.
Die wahrscheinlich einfachste Art, die erstaunlichen Auswirkungen von Quantenphänomenen einzusehen, wurde erst im Jahr 1993 - zunächst als Gedankenexperiment - von A. C. Elitzur und L. Vaidmann angegeben. (Das zeigt übrigens, daß auch die professionellen Physiker viele Jahrzehnte lang den alten Anschauungen verhaftet waren). Sie ist in eine etwas plakative Geschichte eingebaut: Stellen wir uns vor, wir hätten einen Vorrat an Bomben einer extrem sensiblen Bauart. Jede Bombe hat einen Zünder, der die Explosion auslöst, sobald ihn auch nur ein einziges Photon trifft. Über diesem Zünder ist eine Schutzkappe angebracht, die verhindert, daß die Bomben beim ersten zufälligen Eintreffen eines Photons explodieren. Nun ist aber bei der Produktion der Bomben ein Malheur passiert: einige haben überhaupt keinen Zünder, sondern nur die Schutzkappe - sie sind also nicht zu gebrauchen . Alle Bomben sehen von außen gleich aus, nur manche haben unter der Schutzkappe einen Zünder, andere nicht.
Haben wir prinzipiell die Möglichkeit, von zuminderst einigen Bomben festzustellen, daß Sie einen Zünder haben? Wir wollen das natürlich tun, ohne sie zu durch eine Expolsion zu verlieren! Im Bereich der klassischen Physik ist das nicht möglich: Um nachzu-sehen, ob eine Bombe einen Zünder besitzt, müssen wir sie an-schauen, und dazu müssen wir zumindest ein Photon verwenden, das zuerst den Zünder trifft und dann in ein Auge (oder einen Detektor) fällt.
Die Quantentheorie gibt uns erstaunlicherweise eine Möglichkeit
Bomben mit Zünder zu finden, und diese ist recht einfach: wir plazieren
eine zu testende Bombe in den oberen Strahlengang unseres Interferometers
(und nehmen an, daß der Test ansonsten im absolut Dunkeln stattfindet,
so daß keine weiteren Photonen ihn stören können):

Insgesamt kann also beim Bombentest folgendes passieren:
So gut, so schön.
Wer hartnäckig ist, betrachtet eine der entdeckten Bomben mit Zünder nachdenklich und fragt: Woher wissen wir eigentlich wirklich, daß der Zünder unter der Schutzkappe exitiert? Wir wissen es sicher nicht von einem Ereignis am Ort des Zünders, denn dort ist nichts passiert! Wäre ein Photon dort gewesen, wäre die Bombe ja explodiert. Quantenmechanische Phänomene können nicht-lokal sein: sie können uns etwas über Raumgebiete sagen, von denen gar eine "Ursache" (im üblichen Sinn) ausgegangen ist. Wir wissen von der Existenz des Zünders, weil die Möglichkeitswelle unterbrochen war, d.h. weil das Photon die Bombe hätte treffen können (was es aber nicht getan hat). Eine pure Möglichkeit hatte also physikalische Konsequenzen! Damit ist die übliche Beziehung zwischen "Ursache" und "Wirkung" (also der Begriff der Kausalität) durcheinander geraten. Man kann es vielleicht so sehen, daß das System als Ganzes über die Existenz des Zünders "weiß". Information dieser Art bezteichnet man als Quanteninformation. (Experimente vom Bombentest-Typ heißen übrigens "wechselwirkingsfreie Messung". Entgegen einer weitverbreiteter Auffassung, die auf Werner Heisenberg zurückgeht, ist es möglich, Informationen aus einem System zu erhalten, ohne es zu beeinflussen).
Denkaufgabe: Wird eine große Zahl von Bomben auf diese Wiese untersucht, so wird etwa ein Viertel aller Bomben mit Zünder entdeckt, ohne zu explodieren. Wenn die Bomben, über die keine Aussage möglich ist (Klick in Detektor 2) "recycelt", d.h. dem Test erneut zugeführt werden, und die verbleibenden unentschiedenen wieder getestet werden ect. ect. - wie groß ist schlußendlich die Ausbeute? (Antwort: ein Drittel. Die Problemstellung führt auf eine einfache geometrische Reihe).
Wenn übrigens nach erfolgter Aufdeckung der Existenz eines Zünders
einfach die Schutzkappe entfernt wird, können die Bomben zu guter
Letzt noch zu einem friedlichen Zweck verwendet werden: sie testen die
Quantentheorie. Denn wenn unter der Schutzkappe einer solchen Bombe
kein Zünder wäre, so wären unsere Annahmen über die
Rolle der Welle als Maß für die Wahrscheinlichkeit von Ereignissen
falsch gewesen. Realistische Experimente werden nicht mit Bomben, sondern
mit den (vergleichsweise unspektakulären) Photonen durchgeführt.
Die Polarisation des Lichts, die wir bisher völlig außer acht
gelassen haben, spielt in ihnen eine wichtige Rolle. (Photonen besitzen
einen Eigendrehimpuls, den Spin, der in der Quantentheorie an die Stelle
der Polarisation tritt). Derartige Experimente sind unter anderem von einer
Forschungsgruppe um Anton Zeilinger an der Universität Innsbruck durchgeführt
worden. In allen, auch reichlich ausgeklügelten Experimenten
haben wir bisher immer eine Bestätigung der quantentheoretischen
Grundannahmen erhalten.
Weitere mögliche Kapitel, skizziert:
8. Materiewellen
Hier kann aufgrund der Einfachheit der klassischen
nichtrelativistischen Mechanik besser auf quantitative Zusammenhänge
eingegangen werden (de Broglie-Beziehung) als im Zusammenhang mit
Photonen. Auch wird das Plancksche Wirkungsquantum
eine prominentere Rolle einnehmen als bisher.
Bestimmung des Impulses aus einem gegebenen Wellenmuster
(wichtig für eine begrifflich korrektere Fassung der Unschärferelation
als dies allgemein üblich ist).
Vereinfachte Konzeption der Schrödingergleichung
(als Energie-Impuls-Beziehung = Frequenz-Wellenlängen-Beziehung
für Materiewellen).
9. Heisenbergsche Unschärferelation
Ort-Impuls-Unschärferelation als Eigenschaft
von Wellen (nicht von Messungen!)
Zeit-Energie-Unschärferelation (als
"Energie-Ausborgen" in "klassisch verbotenen Prozessen").
Tunneleffekt (mit Hilfe der Zeit-Energie-Unschärferelation
als "Energie-Ausborgen"), Anwendung: Transistor.
10. Das Atom
Stehende Wellen(funktion), Energieniveaus, Spin,
Bosonen und Fermionen, Pauli-Verbot, Ursprung der Atomspektren, Ionisierung,
physikalische Basis für das Periodensystem der Elemente.
Photoelektrischer Effekt.
11. Die Stabilität der Materie
Aufenthaltswahrscheinlichkeit des Elektronen im
Atom, Orbitale, chemische Bindungen.
Kristalle: Energieniveaus und Bändermodell.
12. Quantentheorie großer Systeme
Das Plancksche Strahlungsgesetz.
Die verschiedenen Eigenschaften von Fermionen
und Bosonen.
Bose-Einstein-Kondensation.
Fermigas (Bezug zu Neutronensternen und Gravitationskollaps).
13. Makroskopische Quantenzustände
Supraleitung, Superfluidität, Laser.
14. Verschränkte Zustände, EPR-Experimente, Quantencomputer, Quanten-Teleportation
Hier wäre die Entwicklung zeitgemäßer
didaktischer Konzepte besonders wünschenswert, da diese Themen allerneueste
Entwicklungen widerspiegeln. Sie sind in den Medien präsent und ziehen
(zurecht) die Aufmerksamkeit vieler junger Menschen auf sich.Über
weite Strecken wird man diese Themen (entsprechend vereinfacht) anhand
Interferometer-ähnlicher Anordnungen wie der oben besprochenen - und
des Quanten Zenon-Effekts - diskutieren können. Eine etwas tiefere
Behandlung des Begriffs der Polarisation (d.h. des Spins) scheint dafür
aber notwendig zu sein. Besondere Schwierigkeit: Die Nicht-Vertauschbarkeit
der Spin-Komponenten, die ja der eigentliche Grund für das "EPR-Paradoxon"
sind.
Es steht bereits einiges an halbwegs verständlicher
Literatur zur Verfügung. Allerdings zeigen gerade diese Themen, daß
ein gewisses Umdenken, was eigentlich die Hauptinhalte die Quantentheorie
sind, notwendig ist.
15. Quantentheorie von Elementarteilchen
Elementarteilchenreaktionen, Betonung der Zeit-Energie-Unschärferelation
als "Energie-Ausborgen", virtuelle (insbesondere klassisch verbotene)
Prozesse, Relativitätstheorie und Quantentheorie, die Bedeutung der
Formel E = mc^2 in diesem Zusammenhang, Idee der Feynman-Graphen.
Idee der "Quantenfelder".
16. Quantengravitation - die Grenzen der Begriffe Raum und Zeit
Ist die Vorstellung der Gravitation als Geometrie
der Raum-Zeit grob bekannt und steht der Ausdruck für den Schwarzschildradius
eines Schwarzen Lochs zur Verfügung, so kann (begrifflich schwer,
aber rechnerisch leicht) die Größe der Unbestimmtheit von Raum-
und Zeitangaben abgeschätzt werden. (Resultat: Plancklänge und
Planckzeit). Sogar das Problem der kosmologischen Konstante kann ohne fast
ohne mathematischen Aufwand dargestellt und diskutiert werden. Auch ist
es - wenn die Vorstellung von virtuellen Prozessen verwendet werden kann
- nicht schwierig, durch Plausibiliätsüberlegungen die Temperatur
eines Schwarzen Loches (Hawking-Effekt) zu abzuschätzen. Für
all diese Anwendungen ist an quantentheoretischen Beziehungen nur die Zeit-Energie-Unschärferelation
notwendig.
Raum-Zeit-Schaum, Wurmlöcher.
17. Die totale Quantenwelt und das Problem der Messung
Die Diagramme 2 - 5 zeigen die eigentümliche Rolle der Messung in der Quantentheorie: Von Messung (oder Beobachtung) wird immer dann gesprochen, wenn ein Strahlengang einfach unterbrochen wird. Diese Unterbrechungen finden innerhalb der Detektoren (oder durch die Bombe) statt. Sie stellen in gewisser Weise Vorrichtungen dar, die Photonen (oder auch andere Teilchen) zwingen, "laute", also makroskopische und klassische Antworten zu geben. ("Ich bin hier" übersetzt sich in einen Detektorklick oder in die Explosion der Bombe). Dieser Vorgang heißt in der Kopenhagender Interpretation der Quantentheorie (Niels Bohr) der Kollaps des Wellenfunktion. Dabei wird aber auf eine etwas künstlich Art eine Trennung zwischen Quantenobjekten einerseits und klassischen Objekten (Meßgeräten, Bomben) andererseits eingeführt. Wodurch letztere in der Lage sein sollen, aus Quantensystemen klassische Antworten herauszupressen, bleibt unklar. Damit werden die Begriffe Beobachter und Messung äußerst problematisch.
In einer wirklich einheitlichen Sichtweise müssen alle Teilsysteme, also auch Beobachter und Meßgeräte, als Quantenobjekte begriffen werden. Das entspricht der simplen Aussage, daß Strahlengänge eigentlich gar nicht unterbrochen werden können! Denn auch innerhalb eines Detektors geschehen Dinge, die der Quantentheorie unterliegen (daß ein Photon in einer Reaktion zugunsten anderer Teilchen verloren gehen kann, ändert nichts an diesem Argument, wenn der Begriff der Wellenfunktion allgemein genug gehalten wird). Insbesondere in einer Theorie des ganzen Universums ("Quantenkosmologie") hat ein vom eigentlichen Geschehen abgetrennter klassischer Beobachter keinen Platz mehr. Man tendiert heute dazu, den Begriff der Messung als näherungsweises Konzept zu betrachten: Durch die Wechselwirkung mit der Umgebung verhält sich ein System als Ganzes mit sehr guter Genauigkeit (aber eben doch nur näherungsweise) so, als ob es aus einem klassischen Teil (den Beobachter, Meßgeräten und makroskopischen Objekten) und einem Quantenteil (z.B. den Photonen, die im Bombentest verwendet werden) bestünde. Was eine Messung ist, muß also nicht eigens postuliert werden. Es ist eigentlich schon im Konzept der Wellenfunktion enthalten, wurde aber erst in den letzten zwei Jahrzehnten gebührend beachtet. Leider sind zur Demonstration dieses Zugangs,der den Namen "Dekohärenz" trägt, (zumindest bis zur Entwicklung geeigneter didaktischer Konzepte) aufwendige Rechnungen notwendig. Diese Entwicklungen sind insofern bedeutend, als sich damit unsere Vorstellungen von der Einheit und Geschlossenheit der physikalischen Welt abrunden, die Theorien in gewissen Weise "ästhetischer" werden.
Diskussion: Was kann (oder soll) unter dem Schlagwort "Einheit
der Naturgesetze" verstanden werden?
18. An der Grenze zur Biologie - Quantentheorie als Basis für Leben?
Die Fortschritte der Molekularbiologie und das
stetig wachsende Verlangen nach einer einheitlichen wissenschaftlichen
Sicht der Natur machen es unvermeidlich, daß die Grenzen ehemals
voneinander klar geschiedener Gebiete überschritten werden. In den
jüngsten Diskussionen um die Funktionsweise biologischer Systeme und
die Entstehung und Evolution des Lebens ist das bereits spürbar. Obwohl
(oder gerade weil) hier vor allem noch spekulative Ansätze vorliegen,
wird ein interessanter Unterricht nicht um diese Fragen herumkommen, will
er nicht von der pupulärwissenschaftlichen Literatur links liegen
gelassen werden.