Aufgabe: Berechnen Sie das Linienintegral des Vektorfeldes $\vec{F}(\vec{x})=\left(\begin{array}{c}1-y^2\\xy\end{array}\right)$ über
die durch
|
\begin{eqnarray}
x(t) &=& \sin t\\
y(t) &=& 2+ \cos t
\end{eqnarray}
|
|
mit $0\leq t\leq 2\pi$ definierte Kurve $\gamma$!
Berechnung:
- Das Vektorfeld $\vec{F}$ am Kurvenpunkt $\vec{x}(t)$ ist gegeben durch
$$\vec{F}(\vec{x}(t))=\left(\begin{array}{c}1-y(t)^2\\x(t)y(t)\end{array}\right)=
\left(\begin{array}{c}1-(2+\cos t)^2\\\sin t\,(2+\cos t)\end{array}\right)=
\left(\begin{array}{c}-3-4\cos t-\cos^2 t\\2\sin t+\sin t\cos t\end{array}\right)$$
- Mit $\vec{x}(t)=\left(\begin{array}{c}x(t)\\y(t)\end{array}\right)=\left(\begin{array}{c}\sin t\\2+\cos t\end{array}\right)$
ist der Tangentenvektor gegeben durch
$$\dot{\vec{x}}(t)=\left(\begin{array}{c}\cos t\\-\sin t\end{array}\right)$$
- Das gesuchte Linienintegral ist daher gegeben durch
$$\int_\gamma d\vec{x}\cdot\vec{F}=
\int_0^{2\pi} dt\,\,\dot{\vec{x}}(t)\cdot\vec{F}(\vec{x}(t))=
\int_0^{2\pi} dt\,\,\left(\begin{array}{c}\cos t\\-\sin t\end{array}\right)\cdot\left(\begin{array}{c}-3-4\cos t-\cos^2 t\\2\sin t+\sin t\cos t\end{array}\right)=$$
$$=\int_0^{2\pi} dt\,\,\left(-3\cos t-4\,\cos^2 t-\cos^3 t-2\,\sin^2 t-\sin^2 t\cos t\right)$$
- Der letzte Schrit besteht darin, das Integral auch auszurechnen. Eine Möglichkeit, dies zu tun, ist die folgende, ganz direkte:
$$\int_0^{2\pi} dt\,\,\left(-3\cos t-4\,\cos^2 t-\cos^3 t-2\,\sin^2 t-\sin^2 t\cos t\right)=$$
$$=-3
\underbrace{\int_0^{2\pi} dt\,\,\cos t}_{0}
-4
\underbrace{\int_0^{2\pi} dt\,\,\cos^2 t}_{\pi}
-
\underbrace{\int_0^{2\pi} dt\,\,\cos^3 t}_{0}
-2
\underbrace{\int_0^{2\pi} dt\,\,\sin^2 t}_{\pi}
-
\underbrace{\int_0^{2\pi} dt\,\,\sin^2 t\cos t}_{0}
=-6\pi$$
Man kann aber auch vor der Integration den Integranden vereinfachen, etwa indem die Identität
$\sin^2t+\cos^2t=1$ benutzt wird. Damit kann insbesondere $$\cos^3t=\cos^2t\,\cos t=(1-\sin^2t)\cos t=\cos t-\sin^2t\cos t$$
gesetzt werden. Wieso ist das eine Vereinfachung? Weil mit der Identität
$$\frac{d}{dt}\left(\sin^3 t\right)=3\,\sin^2 t\cos t$$
eine Stammfunktion von $\sin^2 t\cos t$ gefunden ist, mit deren Hilfe wir
$$\int_0^{2\pi} dt\,\,\sin^2 t\cos t = \left.\frac{1}{3}\sin^3 t\right|_0^{2\pi} = 0-0=0$$
finden. (Merken Sie sich diesen Trick!) Die Werte der anderen auftretenden Integrals sollte man auswendig wissen, insbesondere
$$\int_0^{2\pi} dt\,\,\sin^2 t=\int_0^{2\pi} dt\,\,\cos^2 t=\pi$$
(was ebenfalls mit Hilfe der Identität $\sin^2t+\cos^2t=1$ bewiesen werden kann).
Zusatzfrage: Um welche Kurve handelt es sich bei dieser Aufgabe?
Antwort: $\gamma$ ist ein Kreis mit Mittelpunkt $(0,2)$ und Radius $1$, der – ausgehend vom
Punkt $(0,3)$ – genau einmal im Uhrzeigersinn durchlaufen wird. Versuchen Sie selbst, das zu begründen!
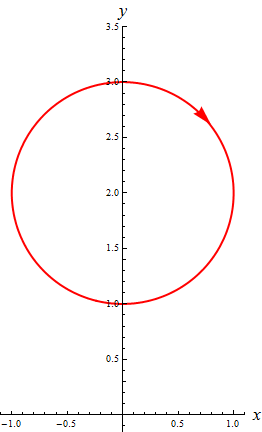 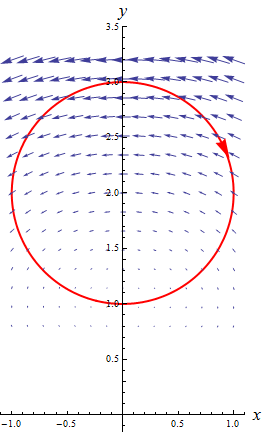
Nachbemerkung:
Die zweite Skizze zeigt zusätzlich das (überall um den gleichen Faktor verkürzte) Vektorfeld $\vec{F}$.
Erkennen Sie "mit freiem Auge" (und ohne jede Rechnung), dass das Linienintegral negativ ist?
Stellen Sie sich $\vec{F}$ als Kraftfeld vor! Dass das Linienintegral negativ ist, bedeutet, dass Sie netto Arbeit
leisten müssen, um ein Teilchen einmal im Uhrzeigersinn um diesen Kreis herumzuführen.
|

