Aufgabe: Interpretieren Sie die durch die Matrix
|
$$T=\left(\begin{array}{cc}
0 & -1\\
1 & 0
\end{array}\right)$$
|
$(1)$ |
definierte lineare Transformation geometrisch! Machen Sie eine Skizze!
Berechnung:
- Wie schauen uns an, wie $T$ auf einen beliebigen (einen "allgemeinen") Vektor wirkt:
$$\left(\begin{array}{cc}
0 & -1\\
1 & 0
\end{array}\right)\left(\begin{array}{c}
x_1\\
x_2
\end{array}\right) = \left(\begin{array}{c}
-x_2\\
x_1
\end{array}\right)$$
- Man könnte nun sogleich erkennen, dass der Vektor auf der rechten Seite auf $\left(\begin{array}{c}
x_1\\
x_2
\end{array}\right)$ normal steht und aus diesem durch eine Linkskippung, also durch eine Drehung um 90° im Gegenuhrzeigersinn,
hervorgeht. Damit wäre die Antwort gefunden, und Sie könnten Ihr Verständnis der Situation durch eine Skizze der Art
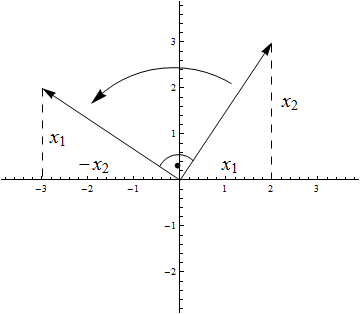
dokumentieren.
- Falls man das nicht erkennt, könnte man sich – um einen Hinweis zu bekommen – die Wirkung von $T$
auf einige konkrete Vektoren ansehen. Am einfachsten ist das für die Vektoren $e_1=\left(\begin{array}{c}1\\0\end{array}\right)$ und
$e_2=\left(\begin{array}{c}0\\1\end{array}\right)$ der Standardbasis, denn deren Bilder unter $T$ sind genau die beiden Spalten von $T$.
Das bedeutet, dass $e_1$ in $e_2$ übergeführt wird und $e_2$ in $-e_1$. Skizze dazu:
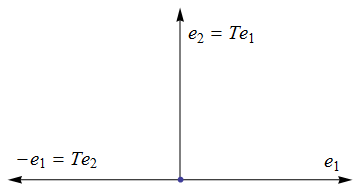
Auf welche Weise geht also $e_2$ aus $e_1$ und $-e_1$ and $e_2$ in geometrischer Hinsicht hervor? Das ist leicht zu erkennen:
Durch eine Drehung um 90° ($\pi\over 2$) im Gegenuhrzeigersinn! $T$ wirkt daher auf die beiden Vektoren der Standardbasis
wie eine Drehung. Da aber nun
- $T$ linear ist,
- da wir wissen, dass auch Drehungen linear sind,
- und da eine lineare Abbildung durch ihre Wirkung auf eine Basis vollständig bestimmt ist,
gilt das auch für alle anderen Vektoren!
- Wenn Sie sich nicht sicher sind, aber immerhin zur Vermutung gelangen, dass $T$ wie eine Drehung um 90° im Gegenuhrzeigersinn
wirkt, können Sie das auch leicht auf eine andere Weise überprüfen, denn Sie sollten
die allgemeine Matrix, die eine Drehung um den Winkel $\alpha$ im Gegenuhrzeigersinn beschreibt, kennen! Sie sieht so aus:
$$\left(\begin{array}{cc}
\cos\alpha & -\sin\alpha\\
\sin\alpha & \cos\alpha
\end{array}\right)$$
Für $\alpha={\pi\over 2}$ geht sie (mit $\sin({\pi\over 2})=1$ und $\cos({\pi\over 2})=0$) genau in $T$ über.
- Die Antwort, wie auch immer Sie sie finden, lautet also: $T$ beschreibt eine Drehung um 90° ($\pi\over 2$) im Gegenuhrzeigersinn. Eine abschließende
Skizze könnte (je nach Lösungsmethode) beispielsweise wie die erste Abbildung auf dieser Seite oder wie
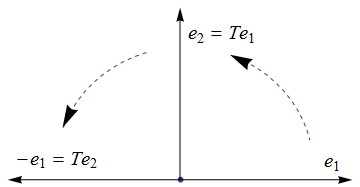
aussehen. Aber auch, wenn Sie anders aussieht, sollte sie das Wesentliche des Ergebnisses zum Ausdruck bringen!
Nachbemerkung: Bei der geometrischen Interpretation einer linearen Transformation, die durch
eine Matrix $T$ definiert ist, ist immer auch ein bisschen Hintergrundwissen nötig! Eine Faustregel besteht darin, so zu beginnen
wie bei der oben vorgeführten Lösungsstrategie:
- Sehen Sie sich die Wirkung von $T$ auf einen allgemeinen Vektor an! Vielleicht erkennen Sie bereits, wie $T$ wirkt. Falls möglich,
machen Sie eine Skizze!
Gehen Sie die wichtigsten Möglichkeiten durch:
- $T$ könnte eine Drehung sein. Beispiel: die obige Aufgabe!
- $T$ könnte eine Spiegelung sein. Beispiel: $T=\left(\begin{array}{cc}
1 & 0\\
0 & -1
\end{array}\right)$.
- $T$ könnte eine Projektion sein. Beispiele: $T=\left(\begin{array}{cc}
1 & 0\\
0 & 0
\end{array}\right)$ und $T={1\over 2}\left(\begin{array}{cc}
1 & 1\\
1 & 1
\end{array}\right)$.
- $T$ könnte Vektoren in leicht erkennbare Richtungen (z.B. entlang der Achsen) strecken bzw. stauchen. Beispiele: $T=\left(\begin{array}{cc}
3 & 0\\
0 & 5
\end{array}\right)$ und $T=\left(\begin{array}{cc}
{1\over 2} & 0\\
0 & 3
\end{array}\right)$.
- Wenn Sie noch nicht draufgekommen sind, sehen Sie sich die Wirkung von $T$ auf die Vektoren der Standardbasis an und machen Sie eine Skizze!
Wenn diese Wirkung mit irgendeiner Ihnen bekannten linearen Transformation $A$ übereinstimmt, so ist $T=A$.
- Wenn Sie zu einer noch nicht hinreichend begründeten Vermutung gelangen, führen Sie eine Berechnung durch!
- Falls Sie vermuten, dass es sich um eine Drehung handelt, vergleichen Sie mit der allgemeinen Drehmatrix!
- Falls Sie vermuten, dass es sich um eine Spiegelung handelt, so versuchen Sie, zu erkennen, an welcher Gerade
gespiegelt wird! (Welche Vektoren gehen in sich selbst über? Auf welche Vektoren wirkt $T$ einfach durch eine Umkehrung der Orientierung?)
- Falls Sie vermuten, dass es sich um eine Projektion handelt, so können Sie das verifizieren, indem Sie überprüfen,
ob $T{\,}^2=T$ gilt. Um die Richtung, in die projiziert wird, und den Teilraum, auf den projiziert wird, zu finden, können Sie die Eigenwerte und
die zugehörigen Eigenvektoren berechnen! Nutzen Sie Ihr Hintergrundwissen, um zu interpretieren, was diese geometrisch bedeuten!
- Auch falls Sie vermuten, dass $T$ in verschiedenen Richtungen streckt/staucht, können Sie die Eigenwerte und Eigenvektoren
berechnen, um nähere Hinweise zu erhalten!
Sie können auch erst einmal die Eigenwerte berechnen und die Möglichkeiten eingrenzen:
- Die Eigenwerte einer Drehung (sie können komplex sein) haben alle den Betrag $1$. Ihr Produkt (inklusive Vielfachheit) ist immer gleich $1$.
- Eine Spiegelung hat Eigenwerte $-1$ und $1$. Das Produkt aller Eigenwerte (inklusive Vielfachheit) ist gleich $-1$.
- Eine Projektion hat nur die Eigenwerte $0$ und $1$.
- Die Eigenwerte einer Transformation, die in verschiedenen Richtungen streckt/staucht, ohne dabei Orientierungen umzudrehen,
sind alle positiv.
Beachten Sie aber, dass die Umkehrungen nicht gelten! So ist etwa nicht jede Matrix, deren Eigenwerte alle den Betrag $1$ haben,
eine Drehung. Beispiel: $T=\left(\begin{array}{cc}
1 & 1\\
0 & 1
\end{array}\right)$ hat nur den Eigenwert $1$, ist aber keine Drehung.
Sie sehen, dass es kein einfaches Kochrezept gibt, aber ein Palette von Methoden, die zur Auswahl stehen, und die Sie nutzen können.
|