Aufgabe: Ermitteln Sie die allgemeine Lösung der Differentialgleichung
$u''(x)+u'(x)+u(x)=0$ in reeller Form ! Berechnen Sie jene spezielle Lösung, für die
$u(0)=1$ und $u'(0)=-{1\over 2}$ gilt!
Berechnung:
- Allgemeine Lösung: Der Exponentialansatz $u(x)=e^{rx}$ fürt auf die charakteristische Gleichung
$r^2+r+1=0$. Sie besitzt die Lösungen $$r_{1,2}=-{1\over 2}\pm i {\sqrt{3}\over 2}$$
Damit sind die zwei komplexen Basislösungen
|
$e^{\left(-{1\over 2}- i {\sqrt{3}\over 2}\right)x}$ und $e^{\left(-{1\over 2}+ i {\sqrt{3}\over 2}\right)x}$
|
$(1)$ |
gefunden. Mit Hilfe der Eulerschen Formel köbnnen sie zu den reellen Basislösungen
|
$e^{-x/2}\cos\left({\sqrt{3}\over 2}x\right)$ und $e^{-x/2}\sin\left({\sqrt{3}\over 2}x\right)$
|
$(2)$ |
kombiniert werden
Die allgemeine Lösung kann daher in der reellen Form
|
$u(x)=e^{-x/2}\left(c_1\cos\left({\sqrt{3}\over 2}x\right)+c_2\sin\left({\sqrt{3}\over 2}x\right)\right)$
|
$(3)$ |
angeschrieben werden.
- Spezielle Lösung: Wir suchen jene Lösung, für die $u(0)=1$ und $u'(0)=-{1\over 2}$ gilt.
Die erste Bedingung kann sofort ausgewertet werden. Mit $u(x)$ von (3) ergibt sich
$$u(0)=c_1$$
Damit ist $c_1=1$ bestimmt. Mit $c_1=1$ reduziert sich (3) auf
|
$u(x)=e^{-x/2}\left(\cos\left({\sqrt{3}\over 2}x\right)+c_2\sin\left({\sqrt{3}\over 2}x\right)\right)$
|
|
Damit müssen wir $u'(x)$ an der Stelle $x=0$ bilden.
Eine kurze Rechnung ergibt
$$u'(x)={1\over 2}\left(c_2\sqrt{3}-1\right)e^{-x/2}\cos\left({\sqrt{3}\over 2}x\right)+\dots$$
wobei die Punkte für einen Term mit $\sin\left({\sqrt{3}\over 2}x\right)$ stehen, der für $x=0$ sowieso
wegfällt. Daher gilt
$$u'(0)={1\over 2}\left(c_2\sqrt{3}-1\right)={c_2\sqrt{3}\over 2}-{1\over 2}$$
Das muss also gleich $-{1\over 2}$ sein, woraus sich sofort $c_2=0$ ergibt.
Die gesuchte spezielle Lösung ist daher gleich
|
$u(x)=e^{-x/2}\cos\left({\sqrt{3}\over 2}x\right)$
|
$(4)$ |
Nachbemerkung 1:
Ein beliebter Fehler besteht darin, in (1) das $x$ zu vergessen. Ein solcher Fehler setzt sich dann
in (2) und (3) fort und verunmöglicht die Berechnung der speziellen Lösung,
weil ja kein $x$ mehr da ist, das $0$ gesetzt werden könnte!
Nachbemerkung 2:
Die Differentialgleichung und die Suche nach der speziellen Lösung können physikalisch so formuliert werden:
Auf ein Teilchen der Masse $1$ wirkt eine harmonische Kraft mit Federkonstante $1$ (und Gleichgewichtslage $0$) sowie eine
zur Geschwindigkeit proportionale Reibungskraft mit
Reibungskoeffzient $1$. Das Teilchen wird zur Zeit $0$ vom Ort $1$ mit Geschwindigkeit $-{1\over 2}$ weggeschossen. Wie bewegt es sich?
Die grafische Darstellung der Lösung (4)
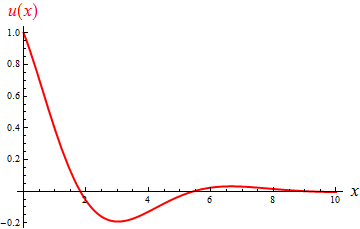
zeigt, dass es sich um eine gedämpfte Schwingung handelt. Beachten Sie, dass $x$ hier die Zeit und $u$ den Ort bezeichnen!
|
