Bisweilen, wenn es um den modernen Stand der Naturgesetze oder um die Möglichkeiten menschlicher Erkenntnis geht, kommt die Rede auf die Quantentheorie. Dann gehen die "Unschärfen" und "Unbestimmtheiten" um, es wird von Teilchen gesprochen, deren Ort man nicht genau kennt, und es ist nicht ganz klar, was man sich darunter am Besten vorstellen soll. Insbesondere stellt sich das Problem, was eine Messung eigentlich ist und zu welcher Art von Wissenszuwachs sie führt. Interessanterweise kann der im vorigen Anschnitt besprochene Satz von Bayes helfen, die Logik, die diesen Begriffen zugrunde liegt, zu verstehen. Wir werden im Folgenden weder die Gesetze der Quantentheorie im Detail wiedergeben, noch sie zu begründen oder zu motivieren versuchen. Statt dessen werden wir einen ihrer wesentlichen Grundzüge beschreiben.

Jedes physikalische System besitzt gewisse Messgrößen (Observablen). Wir ignorieren zwei Raumdimensionen und beschränken uns auf ein Teilchen, d.h. auf ein punktförmiges Objekt. Wir können dabei etwa an ein Elementarteilchen denken, das durch eine Kraft in einem bestimmten Raumgebiet festgehalten wird - daher nennen wir unser System ein eindimensionales Atom. Weiters nehmen wir an, dass es stationär ist, d.h. dass keine seiner physikalischen Eigenschaften von der Zeit abhängt. Und schließlich nehmen wir der Einfachheit halber an, dass der Ort die einzige Observable unseres Systems ist.

Weiters gibt es den Begriff des physikalischen Zustands eines Systems. In der klassischen Mechanik verstehen wir darunter eine vollständige Angabe der Werte aller Observablen - im Fall unseres eindimensionalen Teilchensystems wäre das die Angabe des Ortes, also einer reellen Zahl.

Dabei handelt es sich nicht wirklich um die allgemeinste Bedeutung des Zustandsbegriffs in der Physik, aber darauf kommt es hier nicht an.

In der Quantentheorie hingegen sind nur Wahrscheinlichkeitsaussagen möglich. Ein Quantenzustand (oder eine Wellenfunktion) ist eine Vorschrift, die jeder Observablen eine Wahrscheinlichkeitsverteilung zuordnet. (Im Fall des Ortes sprechen wir einfach von der Ortsverteilung). Wird eine Observable gemessen, so ist das Resultat ein Zufallswert, der aufgrund der entsprechenden Wahrscheinlichkeitsverteilung zustande kommt. (Vor der Messung ist der Wert der Observable nicht etwa unbekannt, sondern unbestimmt!)

Um Mißverständnissen vorzubeugen: Dabei handelt es sich um Aussagen einer Theorie (nämlich der Qantentheorie). Sie beschreibt, wie wir zu statistischen Voraussagen über zukünftige Messausgänge kommen. Wie auch immer man über das Funktionieren "der Natur" denken mag - die Quantentheorie hat bisher alle experimentellen Überprüfungen, denen sie unterzogen wurde, bestens bestanden.

Wir machen nun eine weitere Vereinfachung, indem wir diese Wahrscheinlichkeitsverteilungen mit den Zuständen identifizieren.

Eigentlich ist das ein grober Verstoß gegen die Regeln der Quantenmechanik. Die Wellenfunktion für ein Teilchen ist eine komplexwertige Funktion, die nicht nur Informationen über den Ort, sondern auch über alle anderen Observablen beinhaltet. Das Quadrat ihres Absolutbetrags ist die Wahrscheinlichkeitsverteilung für den Ort.

Hier sind vier typische Zustände für unser eindimensionales Atom dargestellt:

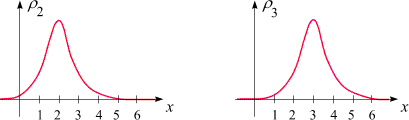
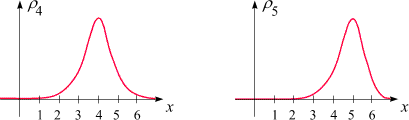
Wir nennen sie r₂, r₃, r₄ und r₅, da ihre Peaks (Erwartungswerte) bei x = 2, 3, 4 und 5 liegen. Ist beispielsweise unser System im Zustand r₂, so wird bei einer Ortsmessung ein Wert x gemäß der Verteilung r₂(x) "gewürfelt". Danach ist das System nicht mehr im Zustand r₂, d.h. die bisherige Wahrscheinlichkeitsverteilung ist hinfällig (in der Praxis ist das System dann oft zerstört). Wir könnten uns dann eine zweite Kopie des System besorgen ("präparieren"), die ebenfalls im Zustand r₂ ist, und wieder eine Messung durchführen. Die auf diese Weise nach vielen Messungen erhaltenen Daten werden sich ungefähr gemäß der Funktion r₂(x) über die x-Achse verteilen (und zwar umso genauer, je mehr Messungen gemacht wurden). So weit, so gut.
 

Was wir bisher besprochen haben, entspricht einer Situation, in der ein bekannter Zustand vorliegt und eine Voraussage über eine zukünftige Messung gemacht wird. Messungen dieser Art dienen nicht dazu, Information über das System zu gewinnen, sondern die Theorie zu überprüfen, Naturkonstanten zu messen oder Ähnliches. Das ist in vielen Fällen genau das, was man braucht, aber nicht immer - denn manchmal hat man es mit einem physikalischen System zu tun, dessen Zustand nicht von vornherein bekannt ist.

So etwas tritt beispielsweise bei der Eichung von experimentellen Aufbauten auf. Soll etwa eine Apparatur auf Knopfdruck Photonen liefern, die alle im gleichen Polarisationszustand sind, so muss zunächst einmal überprüft werden, ob (und mit welcher Genauigkeit) sie das tut. Im jungen Gebiet der Quanteninformation ist die experimentelle Bestimmung eines Zustandes (state determination) eine wichtige Sache, auf der die Zuverlässigkeit von Techniken wie der "Quantenkryptographie" oder der "Quantenteleportation" beruht.

In der klassischen Mechanik ist die Lage klar: Messungen sind dazu da, um den Zustand eines Systems festzustellen. Auch wenn jede Messung das gemessene Objekt beeinflusst, kann diese Wirkung im Prinzip beliebig klein gehalten werden. Für ein eindimensionales Atom ist das Messergebnis idealerweise eine reelle Zahl, die den Ort und daher den Zustand des Systems angibt.

Was aber stellt eine Messung an einem Quantensystem eigentlich fest? Wenden wir die oben skizzierte Theorie auf ein eindimensionales Atom an: Das System befindet sich in einem Zustand, den wir nicht kennen. Das Messergebnis ist eine Zufallszahl, die von einem Prozess herrührt, den wir nicht kennen. Das ist ein klarer Fall für den Satz von Bayes! Vereinfachen wir die Situation, indem wir annehmen, dass das System in einem der vier oben dargestellten Zustände r₂, r₃, r₄ oder r₅ ist. Wenn die Messung das Ergebnis x liefert, so können wir zunächst einmal nachrechnen, für welches j (2, 3, 4 oder 5) die Zahl r_j(x) am größten ist. Dann ist r_j sicher ein Kandidat für den gesuchten Zustand, da in ihm die Wahrscheinlichkeit, x (genauer: einen Wert in einem kleinen Intervall um x) zu erhalten, am größten ist. Wie sicher ist diese Prognose? Logisch betrachtet, stehen wir vor einem Problem, das dem Münze-Würfel-Spiel des vorigen Abschnitts entspricht: Für eine Quantifizierung der Genauigkeit, mit der aus einem Messwert auf einen Zustand geschlossen werden kann, sind Apriori-Wahrscheinlichkeiten vonnöten. Können wir gemäß unserem Kenntnisstand keinen der vier Zustände bevorzugen, so bleibt nichts anderes übrig, als allen die gleiche Apriori-Wahrscheinlichkeit von 1/4 zuzuordnen. Entscheiden wir uns also für irgendwelche Apriori-Wahrscheinlichkeiten und nennen sie P_j, und ist x das Messergebnis, so ist gemäß dem Baysschen Satz die Wahrscheinlichkeit, dass das System im Zustand r_j war, durch

gegeben, wobei c so gewählt wird, dass p₂ + p₃ + p₄ + p₅ = 1 ist.

Wir kommen also zu dem Schluss, dass Messungen an Quantensystemen zwar den Kenntnisstand über den Zustand eines Systems vermehren, diesen aber - im Unterschied zur klassischen Mechanik - nicht eindeutig bestimmen! Haben wir eine Maschine zur Verfügung, die Systeme in immer dem gleichen (zunächst unbekannten) Zustand produziert, so können wir durch genügend lange Messreihen beliebig genau herausfinden, um welchen es sich handelt. Je größer die Zahl der Messungen ist, umso weniger wird es auf die Apriori-Wahrscheinlichkeiten ankommen. Haben wir es hingegen mit einem Prozess zu tun, der alle vier Zustände erzeugen kann, und zwar mit Wahrscheinlichkeiten P_j, so ist (1) das Beste, was wir erreichen können!

Da reale Quantensysteme mehr als nur eine Observable besitzen und diese in verwickelter Weise miteinander verbunden sind, gibt es eine Reihe von Methoden, die Aussagekraft einer Messung hinaufzuschrauben. Aber prinzipielle Grenzen vom Typ (1) gibt es auch dann. Erschwerend kommt hinzu, dass in Wahrheit die Wahrscheinlichkeitsverteilungen nicht mit den Zuständen identifiziert werden können. Selbst wenn die Wahrscheinlichkeitsverteilung für den Ort eines Teilchens bekannt ist, kennen wir damit von der Wellenfunktion nur den Absolutbetrag, nicht aber die Phase. Letztere hängt mit der Wahrscheilichkeitsverteilung anderer Observablen (wie des Impulses) zusammen.
 

Die Quantentheorie plagt die Menschen also mit zweierlei Unsicherheit:

1. In einem gegebenen (bekannten) Zustand sind die Werte der Observablen (bis auf wenige Ausnahmen) unbestimmt. Hierbei handelt es sich nicht um bloße Unkenntnis, sondern um ein tatsächliches Keinen-Wert-haben.
2. Die Bestimmung eines Zustands durch Messungen unterliegt immer statistischen Unsicherheiten, die auf die Unbestimmtheiten 1 zurückgehen. Hierbei handelt es sich um Unkenntnis des wahren Zustands.

Punkt 1 ist die wirklich fundamentale Neuerung, die die Quantentheorie in unser Bild von der Natur eingeführt hat. Problem 2 ergibt sich als Konsequenz daraus. Es wird in der Praxis dadurch abgemildert, dass ein Quantenzustand, der in vielen (identischen) Kopien eines Systems realisiert ist, im Prinzip beliebig genau bestimmt werden kann.

Kleine Nachbemerkung für Kenner: Eine weitere Abmilderung der Problematik wird dadurch erzielt, dass die Unsicherheit 2 in gewisser Weise in den Zustandsbegriff integriert werden kann: Von einer Apparatur, die manchmal r₂, manchmal r₃ erzeugt, wird gesagt, dass sie einen aus r₂ und r₃ bestehenden "gemischen Zustand" erzeugt. Dennoch bleibt der Kern des Problems bestehen: Auch ein gemischter Zustand kann nicht durch eine Messung "bestimmt" werden.
 

Aus theoretischen wie praktischen Gründen treten Gauß-Funktionen oft als Wahrscheinlichkeitsverteilungen auf. Ein nicht untypisches Setting des Problems der Zustandbestimmung könnte so aussehen: Ein Quantensystem sei durch eine Ortsverteilung des Typs

charakterisiert, wobei die Standardabweichung (Schwankung, Breite, Ortsunsicherheit) s bekannt, der Mittelwert a aber nur ungefähr bekannt ist: Er entspringt einem Zufallsprozess mit Normalverteilung um den Mittelwert 0 mit (bekannter) Standardabweichung d:

Das entspricht etwa der Erwartung, dass der Mittelwert a der Ortsverteilung (2) eigentlich 0 sein sollte, aber aufgrund unkontrollierbarer Vorgänge im experimentellen Aufbau einen gewissen Spielraum besitzt, von 0 abzuweichen.

Nun wird ein solcher Zustand erzeugt, und eine Ortsmessung ergibt den Wert x. Welche Wahrscheinlichkeitsaussagen lassen sich über den Zustand machen? Wir setzen der Einfachheit halber s = d = 1. Gemäß dem Satz von Bayes (in einer offensichtlichen Adaptierung auf den Fall einer Apriori-Wahrscheinlichkeitsdichte) ist die Verteilung für die Größe a durch

gegeben, wobei die Konstante c so gewählt wird, dass das Integral über p(a) gleich 1 ist. Einige kleinere Umformungen und eine uneigentliche Integration ergeben

Der wahrscheinlichste Wert für a ist daher x/2 (und nicht x, wie vielleicht intuitiv vermutet), die Schwankung ist mit 2^-1/2 jedoch fast so groß wie die quantenmechanische Ortsunsicherheit s, die wir 1 gesetzt haben.

Übungsaufgabe: Rechnen Sie dieses Beispiel mit allgemeinen Werten von s und d durch! Das Ergebnis sollte sein: p(a) = Gaußverteilung mit Mittelwert d² x/(d² + s²) und Schwankung d s (d² + s²)^-1/2 . Was bedeutet das für die Genauigkeit der Zustandsbestimmung, wenn d viel größer (kleiner) als s ist?