Bibliography

1

L. Andersson and P.T. Chrusciel, On ``hyperboloidal'' Cauchy data for vacuum Einstein equations and obstructions to smoothness of null infinity, Phys. Rev. Lett. 70 (1993), 2829-2832.

2

L. Andersson and P.T. Chrusciel, On asymptotic behavior of solutions of the constraint equations in general relativity with ``hyperboloidal boundary conditions'', Dissert. Math. 355 (1996), 1-100.

3

L. Andersson, P.T. Chrusciel, and H. Friedrich, On the regularity of solutions to the Yamabe equation and the existence of smooth hyperboloidal initial data for Einsteins field equations, Commun. Math. Phys. 149 (1992), 587-612.

4

A. Ashtekar and R.O. Hansen, A unified treatment of null and spatial infinity in general relativity. I. Universal structure, asymptotic symmetries and conserved quantities at spatial infinity, Jour. Math. Phys. 19 (1978), 1542-1566.

5

R. Bartnik, The mass of an asymptotically flat manifold, Comm. Pure Appl. Math. 39 (1986), 661-693.

6

R. Beig, P.T. Chrusciel, and R. Schoen, KIDs are non-generic, Annales Henri Poincaré, in press, (2004), gr-qc/0403042.

7

B. Berger, P.T. Chrusciel, and V. Moncrief, On asymptotically flat space-times with 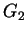${G}_2$ invariant Cauchy surfaces, Annals of Phys. 237 (1995), 322-354, gr-qc/9404005.

8

H. Bondi, M.G.J. van der Burg, and A.W.K. Metzner, Gravitational waves in general relativity VII: Waves from axi-symmetric isolated systems, Proc. Roy. Soc. London A 269 (1962), 21-52.

9

G. Bunting and A.K.M. Masood-ul-Alam, Nonexistence of multiple black holes in asymptotically euclidean static vacuum space-time, Gen. Rel. Grav. 19 (1987), 147-154.

10

P.T. Chrusciel, Boundary conditions at spatial infinity from a Hamiltonian point of view, Topological Properties and Global Structure of Space-Time (P. Bergmann and V. de Sabbata, eds.), Plenum Press, New York, 1986, pp. 49-59, URL http://www.phys.univ-tours.fr/ piotr/scans.

11

to3em, On the invariant mass conjecture in general relativity, Commun. Math. Phys. 120 (1988), 233-248.

12

to3em, On the structure of spatial infinity: II. Geodesically regular Ashtekar-Hansen structures, Jour. Math. Phys. 30 (1989), 2094-2100.

13

P.T. Chrusciel, On uniqueness in the large of solutions of Einstein equations (``Strong Cosmic Censorship''), Australian National University Press, Canberra, 1991.

14

to3em, Semi-global existence and convergence of solutions of the Robinson-Trautman (2-dimensional Calabi) equation, Commun. Math. Phys. 137 (1991), 289-313.

15

to3em, On the global structure of Robinson-Trautman space-times, Proc. Roy. Soc. London A 436 (1992), 299-316.

16

P.T. Chrusciel, Uniqueness of black holes revisited, Helv. Phys. Acta 69 (1996), 529-552, Proceedings of Journés Relativistes 1996, Ascona, May 1996, N. Straumann,Ph. Jetzer and G. Lavrelashvili (Eds.), gr-qc/9610010.

17

to3em, On rigidity of analytic black holes, Commun. Math. Phys. 189 (1997), 1-7, gr-qc/9610011.

18

to3em, The classification of static vacuum space-times containing an asymptotically flat spacelike hypersurface with compact interior, Class. Quantum Grav. 16 (1999), 661-687, gr-qc/9809088.

19

to3em, Towards the classification of static electro-vacuum space-times containing an asymptotically flat spacelike hypersurface with compact interior, Class. Quantum Grav. 16 (1999), 689-704, gr-qc/9810022.

20

to3em, A poor man's positive energy theorem: II. Null geodesics, Class. Quantum Grav. 21 (2004), 4399-4416, gr-qc/0406077.

21

P.T. Chrusciel and E. Delay, Existence of non-trivial asymptotically simple vacuum space-times, Class. Quantum Grav. 19 (2002), L71-L79, gr-qc/0203053, erratum-ibid, 3389.

22

to3em, On mapping properties of the general relativistic constraints operator in weighted function spaces, with applications, Mém. Soc. Math. de France. 94 (2003), 1-103, gr-qc/0301073v2.

23

P.T. Chrusciel, E. Delay, G. Galloway, and R. Howard, Regularity of horizons and the area theorem, Annales Henri Poincaré 2 (2001), 109-178, gr-qc/0001003.

24

P.T. Chrusciel and G.J. Galloway, Horizons non-differentiable on dense sets, Commun. Math. Phys. 193 (1998), 449-470, gr-qc/9611032.

25

to3em, A poor man's positive energy theorem, Class. Quantum Grav. 21 (2004), L59-L63, gr-qc/0402106.

26

P.T. Chrusciel, J. Isenberg, and D. Pollack, Gluing initial data sets for general relativity, Phys. Rev. Lett. 93 (2004), 081101, gr-qc/0409047.

27

to3em, Initial data engineering, (2004), gr-qc/0403066.

28

P.T. Chrusciel, J. Jezierski, and M. MacCallum, Uniqueness of the Trautman-Bondi mass, Phys. Rev. D 58 (1998), 084001 (16 pp.), gr-qc/9803010.

29

P.T. Chrusciel and W. Kondracki, On some global charges in classical Yang-Mills theory, Phys. Rev. D36 (1987), 1874-1881.

30

P.T. Chrusciel and K. Lake, Cauchy horizons in Gowdy space times, Class. Quantum Grav. 21 (2004), S153-S170, gr-qc/0307088.

31

P.T. Chrusciel and O. Lengard, Solutions of wave equations in the radiating regime, Bull. Soc. Math. de France (2003), in press, math.AP/0202015.

32

P.T. Chrusciel, M.A.H. MacCallum, and D. Singleton, Gravitational waves in general relativity. XIV: Bondi expansions and the ``polyhomogeneity'' of Scri, Phil. Trans. Roy. Soc. London A 350 (1995), 113-141.

33

P.T. Chrusciel and R. Mazzeo, On ``many-black-hole'' vacuum spacetimes, Class. Quantum Grav. 20 (2003), 729-754, gr-qc/0210103.

34

P.T. Chrusciel and A. Rendall, Strong cosmic censorship in vacuum space-times with compact, locally homogeneous Cauchy surfaces, Annals of Phys. 242 (1995), 349-385.

35

P.T. Chrusciel and J. Shatah, Global existence of solutions of the Yang-Mills equations on globally hyperbolic four dimensional Lorentzian manifolds, Asian Journal of Math. 1 (1997), 530-548.

36

P.T. Chrusciel and R.M. Wald, On the topology of stationary black holes, Class. Quantum Grav. 11 (1994), L147-152.

37

D.M. Eardley and V. Moncrief, The global existence of Yang-Mills-Higgs fields in 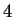$4$-dimensional Minkowski space. II. Completion of proof, Commun. Math. Phys. 83 (82), no. 2, 193-212.

38

H. Friedrich, On the existence of n-geodesically complete or future complete solutions of Einstein's field equations with smooth asymptotic structure, Commun. Math. Phys. 107 (1986), 587-609.

39

S.W. Hawking and G.F.R. Ellis, The large scale structure of space-time, Cambridge University Press, Cambridge, 1973.

40

W. Israel, Event horizons in static vacuum space-times, Phys. Rev. 164 (1967), 1776-1779.

41

S. Klainerman and M. Machedon, Finite energy solutions of the Yang-Mills equations in 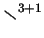${\mathbb{r}}^{3+1}$, Ann. of Math. 142 (1995), 39-119.

42

R. Penrose, Asymptotic properties of fields and space-times, Phys. Rev. Letters 10 (1963), 66-68.

43

to3em, Light rays near 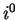$i^0$: a new mass-positivity theorem, Twistor Newsletter 30 (1990), 1-5.

44

R. Penrose, R.D. Sorkin, and E. Woolgar, A positive mass theorem based on the focusing and retardation of null geodesics, (1993), gr-qc/9301015.

45

H. Ringström, Lecture at the Miami Waves conference, January 2004.

46

R. Sachs, Gravitational waves in general relativity VIII. Waves in asymptotically flat space-time, Proc. Roy. Soc. London A 270 (1962), 103-126.