Now we batch together all states having energies
![]() in an interval
in an interval
![]() . The number of states in
such a ``cell'' is named
. The number of states in
such a ``cell'' is named
![]() . The values of
the
. The values of
the ![]() are not important; they should only be large enough to allow
the application of Stirling's formula.
are not important; they should only be large enough to allow
the application of Stirling's formula.
As before we try to answer the question how the ![]() particles should best
be distributed over the
particles should best
be distributed over the ![]() cells. To do so we change the notation
from the one used in Section 2.2, in that we denote the number of
particles in cell
cells. To do so we change the notation
from the one used in Section 2.2, in that we denote the number of
particles in cell ![]() by
by ![]() . The reason for using
. The reason for using ![]() is that
``
is that
``![]() '' is reserved for the quantum numbers.
'' is reserved for the quantum numbers.
A specific distribution
![]() of the
of the ![]() particles to the
particles to the ![]() cells is more probable if its
multiplicity
cells is more probable if its
multiplicity ![]() is larger, meaning that we can allot the
is larger, meaning that we can allot the
![]() particles in more different ways to the
particles in more different ways to the
![]() states in each cell - always keeping in mind the
Fermi or Bose rules:
states in each cell - always keeping in mind the
Fermi or Bose rules:
| (5.1) |
The distribution ![]() having the largest multiplicity
may again be determined by Lagrange variation with the conditions
having the largest multiplicity
may again be determined by Lagrange variation with the conditions
![]() and
and
![]() :
:
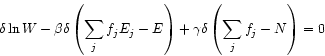 |
(5.2) |
| (5.3) |
For a better understanding of this derivation, let us interpret its
premises as a set of rules in a game of fortune, as we have done in
Chapter 2. By running the applet EFRoulette
we may indeed play that game - for Fermi particles at least - and
compare its outcome with the result just given.
These are the rules:
For non-interacting particles in a square box the ![]() -plane is spanned by integers
-plane is spanned by integers ![]() ; each quantum state is represented by a point.
A specific state of a system of
; each quantum state is represented by a point.
A specific state of a system of ![]() fermions is represented by a set of
fermions is represented by a set of ![]() inhabited points on that plane.
inhabited points on that plane.
To find the average (and also most probable!) distribution of particles on states,
- assign ![]() particles randomly to the states on
particles randomly to the states on ![]() -plane
-plane
- make sure that the sum of the particle energies equals the given system energy,
AND
- discard all trials in which a state is inhabited by more than one particle
- determine the mean number of particles in each state; sort the result according to the state energies
 Applet LBRoulette:
Start
Applet LBRoulette:
Start
|
| Playing the Fermi-Dirac game. [Code: EFRoulette] |