| Franz J. Vesely > CompPhys Textbook > Errata |
|
Home Back to book
Here are a few errata I have detected since publication
Page 34: Equation 2.53 should read $ \begin{eqnarray} a_{ii} \, x_{i}^{(k+1)} &=& b_{i} - \sum_{j > i} a_{ij} \, x_{j}^{(k)} - \sum_{j < i} a_{ij} \, x_{j}^{(k+1)} \; ; \;\;\; i=1,\dots,N \end{eqnarray} $ [May 02; thanks to Steve Knudsen] Page 34: Equation 2.58 should read
$
\begin{eqnarray}
\left[ D + L \right] \cdot x_{k+1}
&=& \omega \, b - \left[ \omega \, R - (1-\omega) \, A \right]
\cdot x_{k}
\end{eqnarray}
$
[and in 2.59, the last $(k)$ should be a superscipt] [May 02; thanks to Steve Knudsen] Page 39: Equation 2.72 should read
$
\vec{h}_{1}= \vec{g}_{1}
-\frac{\textstyle (A \cdot \vec{g}_{1}) \cdot (A \cdot \vec{g}_{0})}{\textstyle
\left| A \cdot \vec{g}_{0} \right|^{2}}
$
(Note that $\vec{h}_{0} \equiv \vec{g}_{0}$).
Accordingly, eq. 2.75 should be
$
\vec{h}_{2} = \vec{g}_{2}
- \frac{\textstyle (A \cdot \vec{g}_{2}) \cdot (A \cdot \vec{h}_{1})}{\textstyle \left|
A \cdot \vec{h}_{1} \right|^{2}}
$
With these corrections the example calculation following eq. 2.77 converges
faster - as it should.
[Sep 04; thanks to Greg Hammett] Page 82: The last five lines should read: In our simple example the fitness is bound to the value $f_{i} \equiv f(x_{i}^{0})$: the lower $f_{i}$, the higher the fitness of $x_{i}^{0}$. It is always possible, and convenient, to assign the fitness $g_{i} \equiv g(x_{i}^{0})$ such that it is positive definite.
A relative fitness, or probability of reproduction, is defined as
$p_{i} \equiv g_{i}/\sum_{i=1}^{N}g_{i}$. It has all the markings of
a probability density, and accordingly we may also ...
Page 117: Equ. 4.153 should read:
$
q_{n+1}=q_{n}+P(p_{n})\Delta t
\, , \;\;\;\;
p_{n+1}= p_{n}+ F( q_{n+1})\Delta t
$
- Somewhat later, the sentence beginning "Incidentally, .." should read:
A very similar first-order symplectic scheme, also
known as the Euler-Cromer algorithm,
$
p_{n+1}= p_{n}+ F( q_{n})\Delta t \, , \;\;\;\;
q_{n+1}= q_{n}+ P(p_{n+1})\Delta t
$
exactly conserves the perturbed Hamiltonian
$
\tilde{H}=H_{ho}-\frac{\textstyle \omega^{2} \Delta t}{\textstyle 2}pq
$
When applied to oscillator-like equations of motion it is a definite improvement over the (unstable) Euler-Cauchy method ... [Dec 03, thanks to Denis Donnelly] Page 154: Equ. 5.137 is printed as
$
\beta_{l}= 2 \cos\left[ \frac{\textstyle 2(l-1)\pi}{\textstyle 2^{p+1}}\right]
$
but should read
$
\beta_{l}= 2 \cos\left[ \frac{\textstyle (2l-1)\pi}{\textstyle 2^{p+1}}\right]
$
Note: the same error appears in Hockney's book. [Jan 04, thanks to the class of 03/04] Page 168: The text following equ. 6.8 should read ... where $u^{*} \equiv u_{LJ}/\epsilon$ and ... [Oct 03] Page 187: Eq. 6.60: the second term in the brackets should read
$
\sum_{\vec{n}} \frac{\textstyle L^{3}}{\textstyle |\vec{r}_{i,j,\vec{n}}|}
F(\eta |\vec{r}_{i,j,\vec{n}}|)
$
[Apr 06] Page 217: Eq. 8.12: should be
$
\begin{eqnarray}
\frac{\textstyle d e}{\textstyle dt} &=& - (e+p) \nabla \cdot v - (v \cdot \nabla)\, p
\\
&=& -e (\nabla \cdot v) - \nabla \cdot (p v)
\end{eqnarray}
$
[May 06] Page 218: Eq. 8.18: first line should be
$
\begin{eqnarray}
e_{j}^{n+1}&=&\frac{1}{2}\left(e_{j+1}^{n}+e_{j-1}^{n} \right)
\\
&&- \dots
\end{eqnarray}
$
[May 06] Pages 223-225: The energy equ. of motion (eqs. 8.52, 8.62 and 8.66) should have a factor $1/2$ on the r.h.s., thus:
$
\frac{\textstyle d \epsilon_{i}}{\textstyle dt} =
- \frac{\textstyle 1}{\textstyle 2} \sum \limits_{k=1}^{N}m_{k}\,
\left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} +
\frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} \right) \, \vec{v}_{ik} \cdot
\nabla_{i}w_{ik}
$
[Aug 08] Page 232: In Figure 8.6 the shading of some cells is barely visible. 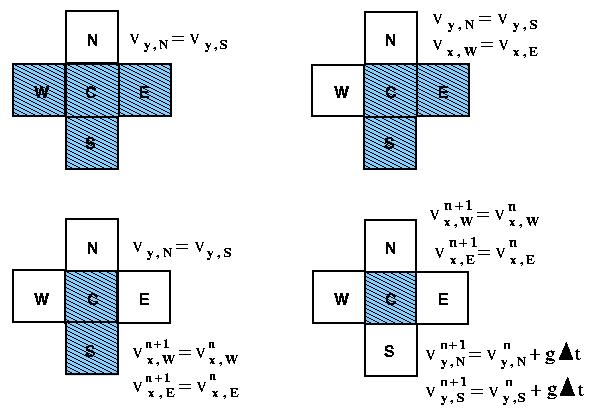
MAC method: the 4 types of surface cells and the appropriate boundary conditions for $v_{x}, v_{y}$ (see POTTER). [May 02] F. J. Vesely / University of Vienna |
