Die Körperlichkeit des Denkens: Erkennen als Begehen eines Weges. Wider das Vorurteil der Körperlosigkeit des Denkens als angebliches ‚Erbe der Philosophie‘ // Performance-Text
Sybille Krämer // Körperlichkeit des Denkens: Erkennen als Begehen eines Weges. Wider das Vourteil der Körperlosigkeit des Denkens als angebliches ‚Erbe der Philosophie‘ (Transkription des Vortrages) // Philosophy On Stage #3
– Wider das Vorurteil der Körperlichkeit des Denkens als angebliches „Erbe der Philosophie“
Es gibt in Bezug auf die Philosophie mindestens 2 Vorurteile:
– Das erste Vorurteil besagt, dass ein Gutteil der Philosophie kategorisch zwischen Körper und Geist trennt;
– Und das zweite besagt, dass die abendländische Philosophie diese Trennung überhaupt erst ins Leben gerufen hat;
Das 1. Vorurteil besagt, dass wenn Philosophen dann doch dem Sehen, dem Wahrnehmen – unseren Augen Gewicht geben – sie in Wahrheit damit das ´geistige Auge´ meinen.
– Und weil die ´Eule der Minerva´[1] immer erst im Dunkeln aufbricht, lautet dann dieses Vorurteil: „Das geistige Auge sieht um so besser, je mehr die leiblichen Augen geschlossen bleiben!“
Heute Abend möchte ich ein Stück weit zeigen, dass diese beiden Vorurteile nicht zutreffen!
Jetzt wäre es nicht schwer, das anhand von Philosophen, wie Nancy, Derrida oder auch Nietzsche zu zeigen.
Es lässt sich aber zeigen, dass genau bei jenen Philosophen, von denen man sagt, dass sie diese „Körper-Geist-Trennung“ überhaupt erst eingeführt und stabil gemacht haben, Anstrengungen zu finden sind, diese Trennung in ihrer eigenen Philosophie und Erkenntnistheorie auch aufzuheben.
Das wesentliche Argument, dass man für die ´abendländische Philosophie´ vorbringen kann, um das zu verstehen, ist, dass man sich klar machen muss – und ich weiß nicht, ob dies auch für die ´östliche Philosophie´ zutrifft – dass viele Philosophen das Denken und das Erkennen als einen Weg auffassen.
Wege sind etwas räumliches! – Wege werden durch Körper gebahnt und begangen.
Und damit einem das klarer wird, sollte man sich vorstellen, dass das, was im Denken geschieht, einer Art Begehung eines Weges gleicht;
Ein auffallendes Merkmal – nicht nur – der Philosophie ist, dass immer wenn sie unsichtbare Sachverhalte behandelt – also theoretische Gegenstände – sie dies mit Hilfe von Raum-Relationen macht.
D. h. abhängig von der Idee – das Denken sei ein Weg – gewinnt Räumlichkeit als eine Art Matrix zur Ordnung der Gedanken eine ganz besondere Rolle.
Und dass dies sowohl unser Denken über die Zeit betrifft, dass wir immer im Zeit-Punkt, Zeit-Raum, Zeit-Intervall, dass wir immer per Räumlichem, wenn wir über die Zeit denken und sprechen, macht so ungefähr klar, was ich damit meine.
Also die Räumlichkeit ist eine primäre Ordnungsform des Denkens – abhängig davon, dass Denken als gehen eines Weges gedacht wird …
Wenn man jetzt über Räumlichkeit und Körper nachdenkt ist Eines ja auffallend: Unser Körper ist die elementare, sozusagen archaische Matrix, mit der wir, den uns umgebenden Raum gliedern; Für mich gibt es jetzt hier rechts und links, vorne, hinten, oben und unten. Mehr binäre Ordnungsformen anhand meiner Körperlichkeit im Raum zu finden, wird ihnen schwer fallen.
Tatsächlich ist unser Körper das erste Instrument – sozusagen – mit dem wir den uns umgebenden Raum strukturieren – in Bezug auf die Stellung, die ich in eben diesem Raum inne habe.
Wenn das aber so ist, dass der Körper eigentlich ein wunderbares Muster, Modell oder Instrument ist, um in räumlichen Zusammenhängen Ordnung zu stiften, dann liegt es überaus nah, wenn denn jetzt auch das Denken in einer Art von Denkraum stattfindet, liegt es überaus nah, diese Matrix, die wir von unserem Körper kennen, genau auf das zu übertragen, dass wir normalerweise als irgendwie unsichtbare Erfahrung oder einen unsichtbaren Prozess erfahren würden.
Begriff: Kartographischer Impuls
Jetzt kommen wir zur These: Wenn es so ist, dass Raum-Relationen ein bevorzugtes Medium sind, zum größten Teil unräumliche Sachverhalte darzustellen, dann kann es sein, dass es so etwas, wie einen „kartographischen Impuls“ in der Philosophie gibt. Ein „kartographischer Impuls“, der etwas zu tun hat mit unserer Erfahrung des Körpers, in dem ihn umgebenden Raum.
Was versteht man unter einem „kartographischen Impuls“?: Wir alle kenne Karten – Netz-Karten von Bus und U-Bahn, Straßen-Atlas und so weiter und so fort … Normalerweise sind wir gewohnt diese Karten, Wanderkarten der Alpen, Stadtpläne usw. … wir sind gewohnt sie als eine Art Struktur-Modelle anzusehen, für das Terrain, dass in dieser Karte in einem kleinem handlichen, flachen Format zur Darstellung kommt.
Aber das ist erst die erste Hälfte der Geschichte, die man über Karten erzählen könnte.
Die zweite Geschichte ist, dass wir Karten gebrauchen um uns zu orientieren, sobald wir ein fremdes, uns unvertrautes Terrain in irgendeiner Weise bewältigen müssen, insofern wir vom Punkt A an dem wir etwa im Moment in einer fremden Stadt, zum Punkt B kommen wollen. Der Witz der Karte besteht also nicht darin ein Territorium einfach abzubilden, sondern er besteht darin, in der Weise ein Territorium tatsächlich strukturell zu repräsentieren, dass ein Nutzer, der sich bewegen im fremden Territorium will, dies mit Hilfe der Karte auch vermag.
Der ´kartographische Impuls´ besteht darin, dass wir ein Modell eines Weltausschnittes haben. D. h. eben Untergrundbahn oder der Luftraum, des Ozeans oder der terrestrischen Welt … Wir haben ein Modell der Welt … wir müssen uns Selber – unseren Leib – in dieser graphisch strukturell abgebildeten Welt indexikalisch verorten.
– Das ist der rote Punt, etwa auf den öffentlichen Stadtplänen. Und wenn uns dieses gelingt, dass unser Körper, der einen Standpunkt im Realraum hat, dann nochmal als Punkt in der Karte wiedergefunden wird, dann können wir diese Karte gebrauchen, um uns im fremden Terrain zu bewegen.
´Kartographischer Impuls´ heißt:
– Entwickle ein Modell der fremden Welt!
– Identifiziere deine Position – das muss man leisten, sonst klappt es nicht –
innerhalb dieser Welt und dann wird es dir gelingen mit Hilfe der Karte eine Bewegung, eine Handlung auszuführen, obwohl du dich überhaupt nicht auskennst und mit dieser Welt überhaupt nicht vertraut bist.
Damit ist diese These klar! Es gibt einen ´kartographischen Impuls´ nun nicht nur in der Geographie, sondern ebenfalls in der Philosophie. Wobei klar ist, dass die Welt, die da zur Abbildung kommt, nicht unsere terrestrische Welt ist, vielmehr die Welt des Philosophen, – eine Wissenswelt – die Welt abstrakter Gegenstände. Das ist die Gelenkstelle meiner Überlegungen.
Und was ich jetzt in aller Kürze zeige ist, dass bei 3 Philosophen, die wir in klassischer Weise als körpervergessen bezeichnen, als jene Philosophen, die das Sinnliche abwerten, um den Geist zu privilegieren, dass genau bei diesen 3 Philosophen sich ein solcher ´kartographischer Impuls´ ausmachen lässt.
Dabei ist mir natürlich völlig klar, dass ich das nur ausgesprochen improvisorisch mache und Ihnen natürlich Begründungen schuldig bleiben muss. Es geht auch nur darum, dass Sie versuchen ein Stück mit mir diese Idee zu denken, was mit der Philosophie geschieht, wenn sie denn beginnt Raum-Relationen einzusetzen, um nicht-räumliche philosophische Sachverhalte und Gegenstände zu ordnen und darin Orientierung zu schaffen.
Diese Idee, dass die Philosophie Orientierung im Denken schafft, ist übrigens eine, die ist auch an der Oberfläche schon nachvollziehbar. Schon Kant hat gefragt, was es heißt sich im Denken zu orientieren?[ – Orient: bedeutet ein Osten] Also schon orientieren ist die Bezugnahme meines Körper auf die Erfahrung von Sonnenauf- und -untergang!
Wittgenstein sagt ebenfalls, dass die Philosophie beginnt, wenn ich sage, „Ich kenne mich nicht aus!“ Er will uns den Weg aus dem „Fliegenglas“[2] zeigen.
Man könnte diese Idee, wie die Philosophie darum ringt den ´Ariadnefaden´[3] zu finden, um an diesem taktilen Instrument, Orientierung zu stiften … das wäre jetzt noch einmal eine andere Geschichte, die ich jetzt aber nicht erzählen will.
Aber es ist damit zumindest klar, dass Philosophie Orientierung stiftet. – Zumindest zu einem Gutteil. Und wenn sie das tut, ist ihre dazu passende Erkenntnistheorie zutiefst infiziert oder auch infiltriert von Raum-Relationen – von räumlichen Verhältnissen – als Ordnungssystem.
Und ich muss jetzt schon fast selber darüber lachen, wie man das so plant – Kant bis Descartes in 10 Minuten – und versucht das so schnell abzuhandeln.
Ich beginne mit Kant: Leider ist das viel zu wenig bekannt, dass es einen letzten vorkritischen Text gibt [ -> siehe Thesenpapier] in dem Kant danach fragt: „Was ist Raum?“
Newton hat den Raum, um es mal so zu sagen, „wie eine hohle Vase gedacht“, in die wir was reinstellen können. Er dachte den „absoluten Raum also als ein Gefäß“!
Leibniz antwortet darauf mit einem „Nein“; Er meint, dass diese Annahme nicht stimme, denn „der Raum sei immer der Zwischenraum zwischen Dingen, die eine Lage haben.“
Und Kant entgegnet wiederum, dass dies von Leibniz schon richtig sei, zu behaupten, dass Räumlichkeit die Tatsache sei und die Dinge eine Lage zueinander haben. Ein Ding kann nie alleine eine Lage haben, sondern immer nur im Verhältnis zu etwas anderem. Kant fügt sogar noch etwas in Bezug auf den Raum hinzu, dass er „Gegend“ nennt.
Und im Unterschied zur ´Lage´ ist die ´Gegend´ etwas, das mit der Ausrichtung zu tun hat, die die Dinge einnehmen. Und diese Ausrichtung – Richtung und Orientierung – so Kant – kann in keiner Weise anders erworben werden, als mit Bezug auf unseren Leib;
Und Kant fährt dann fort: Es gibt eben rechter und linker Hand, es gibt oben und unten … Keine Karte dieser Welt, keine Himmelskarte könnte funktionieren – uns tatsächlich die Lage von Sternen oder Orten auf der Erde erläutern – wenn nicht zugleich ich selbst diese Karte in ein Verhältnis zu mir als Leser oder Nutzer einer Karte setze.
Insofern sagt der (vorkritische) Kant, wo immer etwas im Raume ist, ist es nicht nur in einer Lagebeziehung zu anderen Begriffen, sondern hat außerdem auch eine Richtung inne.
Und diese Richtung ist einzig und alleine durch Bezugnahme auf den menschlichen Leib spezifizierbar. – Sie können nicht objektivieren was rechts und links ist – und wir kennen das alle – sondern es ist überhaupt nur in Bezug auf ihre eigene Körperlichkeit – z. b. auf die Stellung ihrer Hände zu beziehen.
D. h. also, was ich jetzt am Beispiel von Kant – und es gäbe dazu noch sehr viel mehr zu sagen – jetzt nur sagen möchte ist: Kant sagt: Es ist unabdingbar – er macht dies übrigens auch am Beispiel des Schriftstücks klar. Er sagt, wenn wir ein Blatt Papier haben, haben die Zeichen zueinander natürlich eine Lage (nach Leibniz) – Aber wenn ich diese Papier drehe, verändert sich die Lage der Zeichen nicht, jedoch aber die Richtung. Und ein beschriebenes Blatt, wenn ich es denn drehe um 90 oder gar um 180 Grad, wird für die Leser unleserlich.
D. h. also, was ich mit Kant festhalten möchte ist, wo immer unsere dreidimensionale Welt, die orientiert ist an unserem Körper nach oben – unten, rechts – links und vorne – hinten. Wo immer diese Welt in die Fläche geklappt wird, in Form von Bildern, von Graphen, von Diagrammen, von Schriften usw. … wo immer das der Fall ist, kommen wir nicht umhin … immer dann, wenn wir diese Bilder anschauen und lesen bzw. interpretieren … zugleich eine ganz bestimmte Richtung in Bezug auf unseren eigenen Körper darin einzunehmen und diese Richtung auch zu respektieren.
Der Witz dieser Überlegung von Kant ist natürlich folgender. Wenn man etwa der Meinung ist, dass die zweidimensionale Darstellung, die zwischen der einen Dimension der Zeit und der Dreidimensionalität unseres Lebensraumes genau die Mitte einhält. Wenn man also der Meinung ist, dass diese zweidimensionale Darstellung – etwas radikal formuliert – vielleicht das Herzstück wissenschaftlicher Repräsentation ist. Das sie überhaupt Wissenschaft gar nicht machen könnten ohne diese beschrifteten und bebilderten Flächen. Und Kunst übrigens auch nicht!
Wenn man also einen Augenblick diese Selbstverständlichkeit mit der wir mit flachen Welten umgehen noch einmal ins Unvertraute rückt. Und noch einmal darüber nachdenkt, was das eigentlich heißt, dass wir die Zweidimensionalität gebrauchen. – Dann wird einem klar, dass das was Kant sagt, dass auch dieser Bezug auf zweidimensionale Flächen, nicht auskommt ohne Leibbezug.
Die Bezugnahme auf den Körper wird damit gleichsam zu einem Herzstück der wissenschaftlichen Entwicklung.
Bildwelten Descartes
Ich komme jetzt zu Descartes, der immer herhalten muss, für alle Verfehlungen und Verkürzungen der Philosophie. Das Folgende möchte ich bei Descartes klarmachen: Descartes hat in seinen Werken beständig visualisiert. – In der Philosophie werden diese Bilder unterschlagen!
Es gibt also kaum ein cartesisches Werk in dem die Fülle, die absolute Fülle – manche Bilder wiederholt er im ersten Druck auf jeder Seite sieben mal neu. – Also davon abgesehen, dass in der Philosophie diese Bildwelten Descartes kaum auftauchen, bleibt es aber signifikant, dass Descartes ununterbrochen Visualisierungen eingesetzt hat.
Es geht mir nun darum, dass diese Visualisierungen bei Descartes genauso zu verstehen sind, dass sie in Zusammenhang mit der Hand, die etwas tut und dem Auge, das etwas sieht, überhaupt erst wissenschaftliche Objektivität nach Descartes stiftet.
An einem ganz kleinen Beispiel versuche ich das klarzumachen!: An seinem ersten veröffentlichten Werk „Compendium musicae“ – einem musiktheoretischen Werk – das in der Philosophie totgeschwiegen wurde und erst 1978 erstmals auf Deutsch übersetzt wurde.
Was der Witz dieses musiktheoretischen Werkes ist, werde ich jetzt nur ganz kurz andeuten: Descartes versucht akustische Vorgänge in der Zeit – die wir gleichzeitig subjektiv erleben – zum Beispiel als dissonanten oder harmonischen Klang – er versucht diese subjektiven musikalischen Erlebnisse des Menschen – für die Menschenohren – dadurch zu erklären, dass er diese musikalischen Abläufe u. Strukturen ins räumliche, visuelle sozusagen transponiert.
Und damit meint er nicht etwa die Notenschrift; das ist eine andere Form mit der das Auge Eingang findet in wirkliche kompositorische Prinzipien auch der Musik; sondern es geht ihm tatsächlich darum eine „Liniensprache“ zu finden – die Musik gleichsam auf die Linie zu bringen. Sei es auf die gerade oder auch die gekrümmte Linie … Und anhand – das kann ich jetzt nur so kursorisch sagen – anhand bestimmter Linienkonfigurationen zu erklären, wann wir Intervalle als harmonische oder disharmonische empfinden. Ich werde das jetzt hier nicht weiter ausführen!
Ungemein interessant ist, dass Descartes diese Linienkonfiguration wiederum mit den Saiten des Saiteninstruments in Zusammenhang bringt. Und Unterteilungen der Linie, die er vorbringt entsprechen quasi dem, wo der Finger ruht, wenn man ein Saiteninstrument spielt und verschiedene Töne dabei erzeugen möchte. Es gibt also bei Descartes – und das ist ein grundlegendes Motiv – man muss schon fast sagen, die Verschwisterung oder die zwei Seiten einer Medaille – einen ganz engen Zusammenhang zwischen Visualität und dem Haptischem.
Descartes versucht also das musikalische, flüchtige, akustische, unsichtbare Geschehen zu visualisieren – mit der Praxis des Instrumentenspiels korrespondieren zu lassen – und tatsächlich musikalische Zusammenhänge – sozusagen die musikalische Form –zu analysieren. Und zwar in Gestalt räumlicher Relationen innerhalb der Musik.
Hier noch ein Beispiel aus ´Les Météores´ ( = die Meteore): Das ist jetzt ein weiteres Beispiel seiner Visualisierungen. Damit kann gezeigt werden wie weit der Bogen reicht. Dabei geht es jetzt um Meteorologie ( = Wetterkunde); Man muss sehen, dass er nicht ausschließlich Philosoph, sondern Wissenschafter war, der dem Experiment einen ganz hohen Stellenwert gegeben hat.
Descartes versucht eine Hypothese, die er hat – in diesem Fall den Mechanismus der Bewegung kleinster Partikel – zu visualisieren. Also nicht Naturvorgänge oder Phänomene – sondern seine Gedanken, die er in Bezug auf Naturphänomene hat und die er versucht zu visualisieren. Zum Beispiel will er erklären, warum sich Wasser ausdehnt, wenn es verdampft.
Dazu gibt es eine Experimentieranweisung Descartes: Für die Erklärung der Ausdehnung von verdampfendem Wasser, solle man einen Stab nehmen. – Stab und Linie und Faden übrigens ist sozusagen die räumliche Grundmatrix der Orientierung. – Er sagt, man soll einen Stab nehmen und eine Schnur durchziehen; wenn der Stab ruht, dann fällt die Schnur flach und schlaff am Stab herab; wenn man den Stab schnell herumwirbelt, dann beginnt auch die Schnur einen entsprechenden Radius zu beschreiben und alles wegzuschlagen, was im Wege liegt. Und so erklärt er quasi die Bewegung von Wasserpartikeln; In dem Moment, wo Wasserpartikel in Bewegung geraten, müssen sie mehr Raum einnehmen.
Sie merken an diesem einen kleinen Beispiel // Einerseits visualisiert er seine Hypothese – also etwas Unsichtbares; eben eine Hypothese – egal, ob die jetzt stimmt oder nicht; Und andererseits gibt er eine Anweisung, wie jeder in seinem Alltag durch praktisches operieren – diese – seine Hypothese überprüfen könne.
Ganz kurz noch dazu: Descartes hat nicht nur visualisiert und zwar in allen möglichen Formen, von denen ich jetzt nur einen ganz kleinen Ausschnitt erwähnen konnte.
Descartes – und zwar spreche ich hier vom jungen Descartes – hat in seiner Erkenntnistheorie diese Visualisierungspraxis unmittelbar einfließen lassen. Descartes ist der Auffassung, dass es keine Erkenntnis ohne Imagination gibt.
´Imaginatio´ heißt Einbildungskraft! Descartes bestimmt sie als ein körperliches Vermögen. Expressis verbis sagt er, die Einbildungskraft ist körperlich. Und das, was die Imagination macht – wir verwenden heute Imagination eher im Sinne von Einbildung im theorativen Sinne. Für Descartes ist das überhaupt die Grundlage von Erkenntnis. Und er sagt, der Witz der Einbildungskraft ist, dass sie tatsächlich Bilder – also ´figura et extensio, alles gestalten … Die Einbildungskraft arbeitet im Medium von Gestalt und Ausdehnung. Und ehe Descartes überhaupt eine Definition des Körpers gegeben hat – nämlich durch Ausdehnung – hat er gesagt, die Einbildungskraft ist genau die, die genau solche Medien einsetzt.
Also das war im Grunde genommen bei Descartes zuerst mal eine medien-theoretische Aussage, dass zur Erkenntnis, das am Besten geeignet ist, was wir uns vor Augen stellen können, als etwas das Gestalt hat und natürlich als Ausgedehntes auch sichtbar ist. In seiner Frühschrift ´regulae ad directionem ingenii´[4], die erst posthum veröffentlicht wurde, stellt er die Imagination als eine „CONDITIO SINE QUA NON“[5] des Erkennens dar. Und diese Imagination arbeitet sozusagen im Medium dessen, was man als ´Körperliches´ sich vorzustellen hat.
Nun nochmal zu Platon (es geht ja nur darum einmal eine Idee von dem zu bekommen, was das bedeutet, damit, dass die Philosophie keineswegs – in diesen ihren Vertretern – Geist und Körper auseinandergerissen habe.
Jetzt noch schnell zu Platon, bei dem nun wirklich der ´kartographische Impuls´ …
Übrigens (!), das habe ich noch ganz weggelassen; ich meine, Descartes muss mit Mercator[6] in Zusammenhang gesehen werden.
Gerhard Mercator. Kupferstich von Frans Hogenberg 1574
Also jeder dieser Philosophen hat ein Pendant in der Geographie. Also die Weltbildproduktion läuft auf der Ebene der Geographie ganz genauso, wie auf der Ebene der unsinnlichen Gegenstände und der Wissensräume.
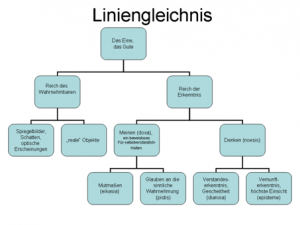
Und jetzt noch schnell zu Platon: Platon hat tatsächlich sein Weltbild visualisiert und zwar in Form eines sogenannten ´Liniengleichnisses´[7].
Abb.: Übersicht zu Platons Liniengleichnis (entnommen aus: wikipedia)
Ich habe natürlich nie ein Bild vom Liniengleichnis gesehen und war völlig überzeugt, dass dieses Liniengleichnis – es stammt aus seinem Werk ´Politeia´ – war natürlich völlig überzeugt, dass das uns nur als Text überliefert ist. Aber es gibt ein Bild dieses Liniengleichnisses aus dem letzten Drittel des 9. Jahrhunderts und zwar in der 11. Handschrift Platons, das in Paris liegt. Man weiß zwar nicht, ob es Platon selbst gezeichnet hat, ausgeschlossen ist es aber nicht.
So, worum es geht ist Folgendes: Platon sagt, dass – auch das Liniengleichnis wäre alleine ein wunderbarer Gegenstand eines eigenen Vortrags – ich kann es jetzt nur ganz kurz machen:
Aufteilung der Linie in Abschnitte
Platon führt die Unterscheidung von ´denkbarer Welt´ und ´sinnlich sichtbare Welt´ ein. Bringt das auf die Linie und sagt hier; Dieser Abschnitt – der kleinere – das ist das sinnlich Sichtbare, der größere – das Unsichtbare;
Dann unterteilt er nochmal beide Abschnitte; Platon gibt damit also ein Linienbild seiner Philosophie. Der Kunstgriff dieses Linienbildes ist, dass er nicht nur seine Ontologie – also wie er sich das Seiende vorstellt – dabei verzeichnet, sondern, dass er zur gleichen Zeit sagt, im Erkennen habe man genau jenen Weg abzuschreiten, den sein Liniengleichnis visualisiert.
Das ist ein Weg, der beginnt bei den Schatten und Reflexen, dann geht er weiter zu den Dingen, Lebewesen, Artefakten und auch natürlichen Lebewesen, kommt dann zu Begriffen und mathematischen Objekten, um schließlich am Ende zu den Ideen vorzustoßen. D. h. aber, dass Platon also ein Bild der Welt gibt, dass auf der Trennung von Körperlichem und Geistigem beruht und diese tatsächlich in die Philosophie einführt; gleichzeitig aber benutzt er diese Karte seiner Philosophie, um klar zu machen, dass man im Denken eine Bewegung zurückzulegen habe, die vom Körperlichen ausgehend Schritt für Schritt weiter zum Ideellen schreitet. Aber das kann mich sich jetzt nicht so vorstellen, als ob man sagen würde, das Körperliche ist der untere Teil und dann im Erkennen kommt es zu dem ideellen höherwertigen. – Sondern Platon zeigt anhand der Mathematik – und die Mathematik ist für ihn eigentlich das, was Wissenschaft bedeutet (Paradigma des Wissenschaftlichen) Er sagt: Kein Mathematiker ist in der Lage über seine allgemeingültigen Gegenstände etwas auszusagen, ohne dass er zugleich diese allgemeinen Ideale und sinnlichen Gegenstände körperlich einzeichnen muss. Es gibt keine Wissenschaft – es gibt keine Mathematik ohne die Konkretion der Abstraktion.
D. h. Platon ist sich völlig bewusst, obwohl er sagt, natürlich ist der Kreis nichts Empirisches. Es gibt keine Kreise in der Welt, die wir sehen. – Dennoch aber der Mathematiker, um zu seinem idealen Kreis zu kommen, muss sich der sinnlichen Vergegenwärtigung seines theoretischen Gegenstandes bedienen. Anders ist Wissenschaft nicht möglich!
Und noch ein Letztes zu diesem Liniengleichnis, das natürlich ganz viele Aspekt enthält. Platon sagt – und das hab´ ich jetzt weggelassen – das ist das innere Konstruktionsprinzip des Liniengleichnisses. Für Platon existiert nur, was zum Bild werden kann.
– Sein ist abbildbares Sein.
Das gilt auch für die Ideen. Es gäbe nicht so etwas wie unsichtbare Ideen, wenn es nicht möglich wäre diese Ideen in Form von realen Verkörperungen sozusagen auch unseren Sinnen vorzuführen. D. h. also, dass für Platon das Bildprinzip zum inneren Prinzip dessen, was überhaupt existiert, wird.
Es gibt bei Platon übrigens viele Visualisierungsszenen. Ich hab jetzt nur das Liniengleichnis als Beispiel genannt.
Jetzt zum Schluss noch zur Geschichte mit dem Sklavenjungen in der berühmten Menon- Szene (ein Gespräch zwischen Sokrates und Menon, in dem Sokrates aufzeigt, dass auch die Verachtetsten seiner Zeit – die Sklaven – Vernunft besitzen):
Ein Sklavenjunge, der nach der These von Sokrates keine Ahnung von Mathematik hat, könne nicht in dem ihm Wissen übertragen wird – also ohne Unterrichtung – nur durch eigene Handhabung und Beobachtung von allen Zeichnungen mathematisches Wissen gewinnen. Und da gibt Sokrates die Aufgabe, er solle ein Quadrat mit einer bestimmten Seite verdoppeln. Der Sklavenjunge denkt zuerst, da muss er einfach nur die Seiten verdoppeln. Zeichnet das hin. Und siehe da – etwas drei mal/vier mal so großes entsteht.
Und der Sklavenjunge merkt also durch eigenes Tun, am Graphismus der Zeichnung, sein Nichtwissen.
Also der erste Schritt ist nicht das Wissen zu kriegen, sondern sein Nichtwissen eingestehen zu können. Es kommt zu jener Stelle wo der Sklavenjunge sagt – er versucht´s mehrmals und scheitert immer wieder; er hat auch alle möglichen Ideen, wie man ein Quadrat verdoppeln kann. Er zeichnet seine Gedanken immer hin. Das ist ja toll, seine Ideen kommen aus dem Kopf in den Sand. Und er sieht da, dass es nicht stimmt. – Und schließlich sagt er, „ich kenn´ mich nicht aus!“ – Und das ist natürlich für Sokrates dann die Aporie[8].
In dem Moment, wo man das eigene Nichtwissen einsieht, ist der erste Schritt getan. Und dann wird Schritt für Schritt weiter aufgebaut.
Sokrates führt den Begriff der Diagonalen ein … und der Sklavenjunge kriegt schließlich durch nachdenken – durch einsetzen seiner Vernunft – raus, dass das Quadrat über der Diagonale eines Quadrates den doppelten Flächeninhalt des ursprünglichen Quadrates besitzt (eine Modifikation des pythagoreischen Lehrsatzes).
D. h. auch hier, bei dieser Menon-Szene sehen wir, wie der Umgang mit sinnlichen Vergegenwärtigungen abstrakter Ideen zur CONDITIO SINE QUA NON wird, um überhaupt diese Ideen denken und fortentwickeln zu können.
ANMERKUNGEN:
[1] Hegel verglich die Philosophie mit der Eule der Minerva. Minerva (lateinisch) war eine römische Göttin, sie entsprach der griechischen Göttin Athene. Jeder römischen Gottheit wurde ein Vogel zugeordnet (zum Beispiel ein Adler dem Jupiter), der Minerva nach dem Vorbild der Athena die Eule, der Vogel der Klugheit. Weil Eulen erst in der Abenddämmerung ihren Flug beginnen, verglich Hegel sie mit der Philosophie, die erst Erklärungen liefern könne, wenn es bereits zu spät für Änderungen sei (am Abend der Geschichte). Philosophen könnten immer nur Vergangenes deuten.
[2] Ludwig Wittgenstein verwendete das Fliegenglas in seinen philosophischen Untersuchungen bildlich: „Was ist dein Ziel in der Philosophie? -> Der Fliege den Ausweg aus dem Fliegenglas zeigen.“ (§309)
[3] Der Ariadnefaden war der griechischen Mythologie zufolge ein Geschenk der Prinzessin Ariadne, Tochter des Königs Minos, an Theseus. Mit Hilfe des Fadens fand Theseus den Weg durch das Labyrinth, in dem sich der Minotauros ( = Mischwesen aus Stierkopf und menschlichem Körper) befand. Nachdem Theseus den Minotauros getötet hatte, konnte er mit Hilfe des Fadens das Labyrinth wieder verlassen. Der Hinweis für die Verwendung des Fadens stammte von Daidalos (deutsch: Dädalus), der auch das Labyrinth entworfen hatte. [Auf dieser Geschichte beruht möglicherweise auch die Redewendung Jemand hat den Faden verloren: Das bedeutet, dass jemand eine Argumentationskette nicht zu Ende führen kann oder sich nicht mehr erinnert, was er zuletzt gesagt hat.]
[4] ´Regulae ad directionem ingeniee´ oder ´Regeln zur Ausrichtung der Erkenntniskraft´ oder ´Regeln zur Leitung des Geistes´ ist eine unfertige Abhandlung über die richtige Methode des wissenschaftlichen und philosophischen Denkens. Dieses Werk legte die Basis für seine späteren Arbeiten über komplexe Probleme der Mathematik, Wissenschaft und Philosophie.
[5] CONDITIO SINE QUA NON = „Ich denke, darum bin ich.“ / also eine Bedingung, ohne deren Erfüllung etwas nicht eintreten kann;
[6] Gerhard Mercator (eigentlich Gerard De Kremer, latinisiert: Gerardus Mercator, deutsch z. T. Gerhard Krämer) (* 5. März 1512 in Rupelmonde, Grafschaft Flandern; † 2. Dezember 1594 in Duisburg, Vereinigte Herzogtümer Jülich-Kleve-Berg) war ein Mathematiker, Geograph, Philosoph, Theologe und Kartograf, der schon zu Lebzeiten als der Ptolemäus seiner Zeit angesehen wurde. Früher vorwiegend als Kartograf und Globenhersteller bis hinein in die arabisch-islamische Welt bekannt, war Mercator im 16. Jahrhundert jedoch vor allem (auch) als Kosmograf, Theologe und Philosoph von großer Bedeutung, was erst durch neuere Forschung deutlich gemacht worden ist. Laut John Vermeulen hat Mercator mit seinem Zeitgenossen Abraham Ortelius zusammengearbeitet.
[7] Das Liniengleichnis ist ein Gleichnis Platons aus seinem Werk Politeia[1] (380 v. Chr.). Im Gleichnis ordnet Platon Sichtbares und Denkbares von unsichersten Vermutungen bis zur sichersten Vernunfterkenntnis, von der abhängigen bildlichen Wahrnehmung bis zur voraussetzungslosen Ideenschau. Jeder Seinsart entspricht dabei eine Erkenntnisart. Grundlegend ist die Unterscheidung zwischen doxa, dem Meinen, und noesis, dem Denken. Über allem steht die Überwirklichkeit der Idee des Guten, in der alles Sein den Urgrund hat und die nur durch die Vernunft geschaut werden kann. Das Liniengleichnis ist das zweite der drei bekanntesten Gleichnisse Platons. Am Ende des sechsten Buches der Politeia folgt das Liniengleichnis dem Sonnengleichnis und mündet dann am Anfang des siebten Buches in das Höhlengleichnis.
[8] Unter Aporie (griech. ἀπορία (aporía), Ratlosigkeit, von gr. o πόρος, der Weg, a poros eigtl. „Ausweglosigkeit“, „Weglosigkeit“) versteht man ein in der Sache oder in den zu klärenden Begriffen liegendes Problem oder eine auftretende Schwierigkeit, weil man zu verschiedenen entgegengesetzten und widersprüchlichen Ergebnissen kommt. Bei Sokrates ist die Aporie eine unauflösbare theoretische Problemstellung, die die paradoxe Erkenntnis des eigenen Nichtwissens ermöglich
Comments are closed.