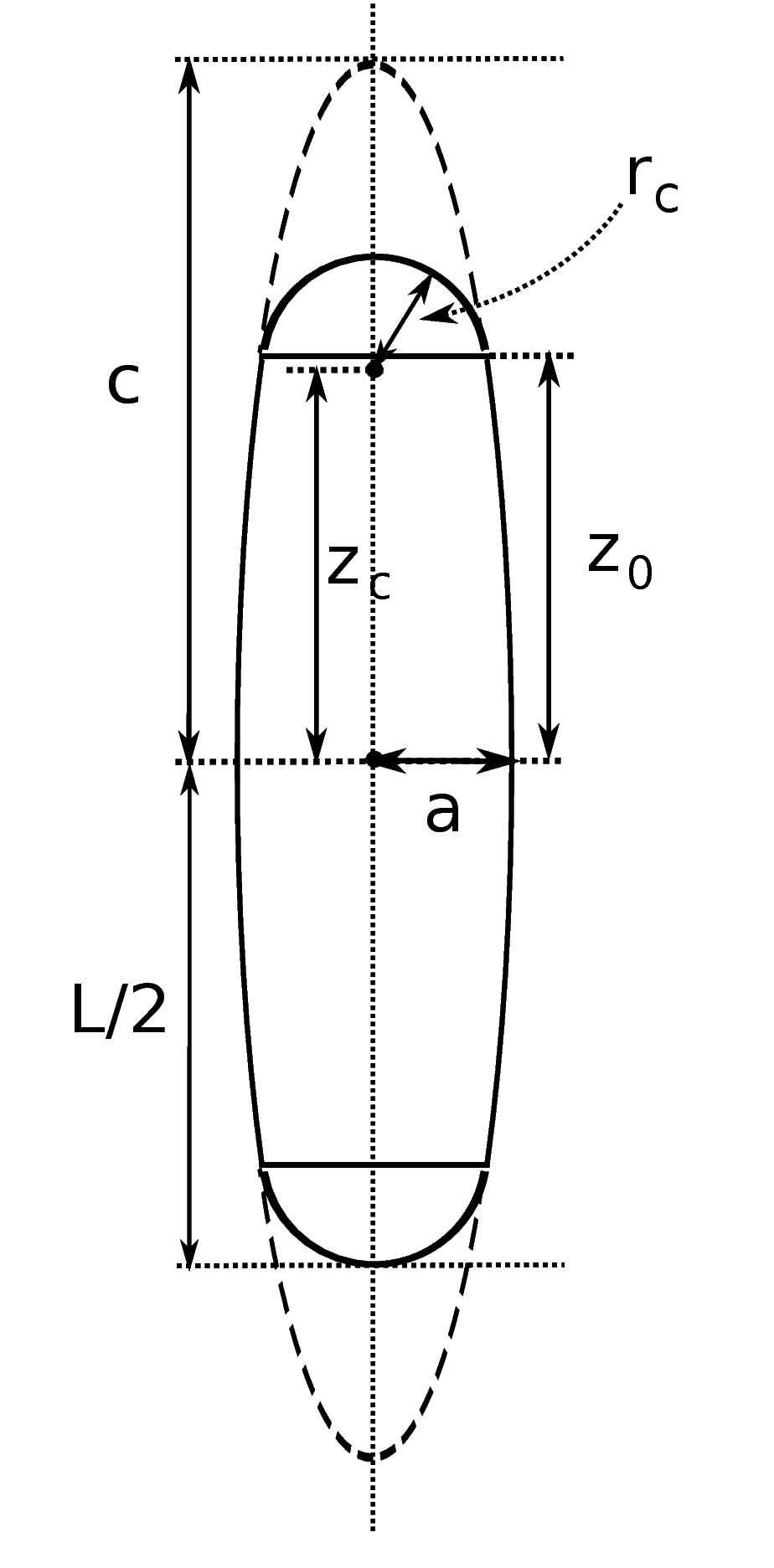
Figure 1: Definitions
Spheroellipsoids
Truncated ellipsoid capped by sphere segments; where the caps are fused to the body they have the same tangent as the ellipsoid.Advantages:
- (a) convex everywhere
- (b) only one additional parameter ($z_{0}$, see below)
- (c) shape may be tuned between spherocylinder and ellipsoid
- (d) not homeomorphic to a sphere (like the ellipsoid); may therefore have a smectic phase
- (e) physically more reasonable than spherocylinders, as many mesogens have a bulge around the waist
Equations:
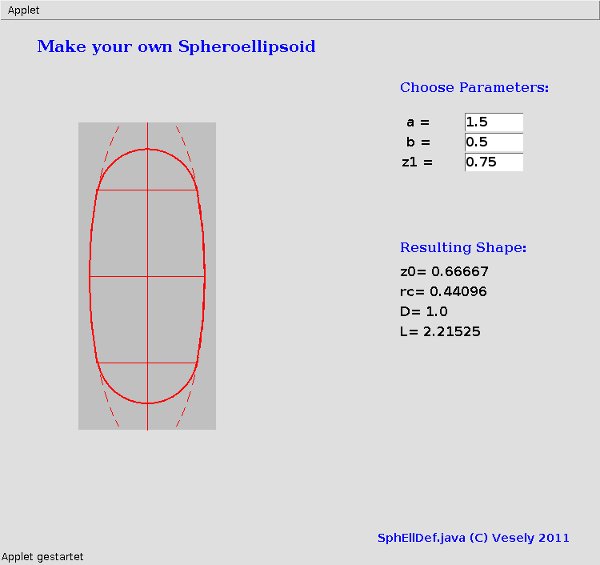
Given long and short semiaxes $c$ and $a$ and a truncation half length $z_{0}$ we have
$z_{c}=z_{0}(1-a^{2}/c^{2})$ ... center of cap
$r_{c}^{2}=a^{2}[1-(z_{0}^{2}/c^{2})(1-a^{2}/c^{2})]$ ... radius of cap
$D=2 \, a$ ... particle width
$L=2 \, (z_{c}+r_{c})$ ... particle length

Figure 2: Hard spheroellipsoid with $c/a=6.0$, $z_{0}/a=3.06$
Here is an Applet to try out various shapes:
Contact Distance between Convex Bodies
This is a fascinating topic, and I will prepare a thorough treatment in a further communication. Here, for the time being, is an Applet for determining the contact distance between two SpheroEllipses:
|
Here is some Fortran code (version 12.11)
[untar -> read README -> play!] |