| |
HSCM News
Jan 2008
|
(Let us forget the previous, OK?)
Some results of Koda theory
- Bare Cylinders, mixed:
Let $l_{1},l_{2}$ be the lengths of the longer and shorter cylinders, and
$d_{1},d_{2}$
the respective diameters; $X=N_{2}/N$ is the relative concentration of
the shorter species.
Fixing $l_{1}=10$, $d_{1}=d_{2}=1$ we may scan the remaining 2d parameter
space $[l_{2,}X]$ for smectic and/or smectically demixed (S2) states.
In Figure 1 all possible S2 states -- i.e. those with $det(S)=0$ and
an apparent instability towards demixing, $ -s11/s12$ < $0$, --
are indicated by a $z$ value of 1 while for S1 and N states $z=0$.

|
|
Figure 1: "Phase surface" of the $l_{1}=10$, $d_{1}=d_{2}=1$
BC (bare cylinders) system.
|
There are two regions where the S2 phase apparently becomes destabilized:
one is $2.$ < $l$ < $3.$ and the other, $3.8$ < $l$ < $4.$. The small $l_{2}$
range resembles the original Koda system where one of the particles is
spherical. This should be investigated some more; for now let us
look at the $l_{2} \approx 4$ region.
Is there really an S2 phase here?
If the discontinuities in Figure 1 were due to S1/S2 or N/S2 transitions
we should also see jumps in the transition packing fraction $\eta$ and the smectic
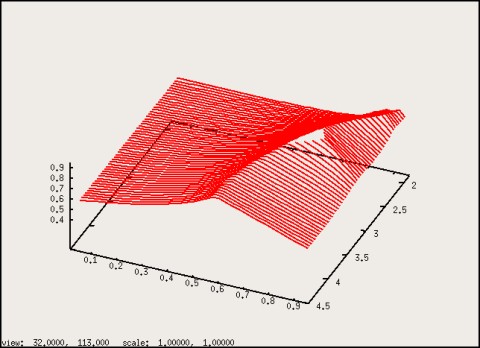
layer distance $\lambda$. As Figure 2 shows, $\eta $ is quite smooth. The triangular
"plateau" near $l_{2}=3$ is due to the fact that I have cut off unphysical
values of $\eta$>$0.96$.
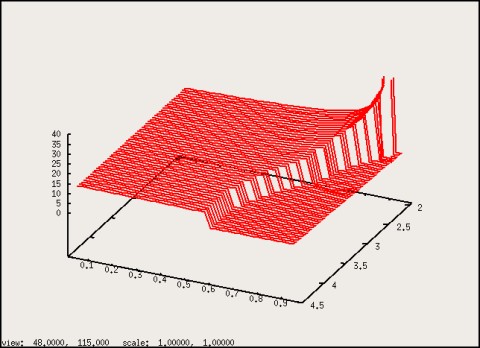
The smectic wave length $\lambda$ is also smooth, with no distinct feature such
as a jump from $ \lambda \approx l_{1}$ to $ \lambda \approx l_{1}+l_{2}$, as might
be expected for a sudden transition S1 --> S2.
|
|
|
Figure 2: Transition density $\eta(l_{2},X)$
|
|
Figure 3: Smectic period $\lambda$ as a function of $(l_{2},X)$.
|
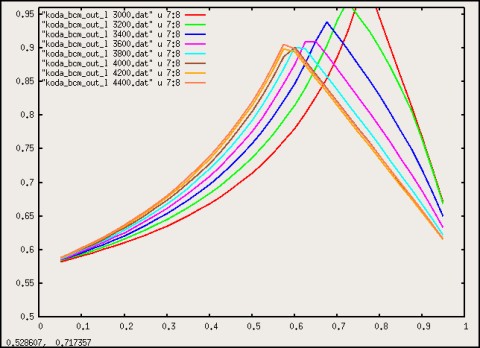
Figures 4 and 5 show a few cross sections of the above surfaces, for a more
quantitative comparison with Szabi's results.
|
|
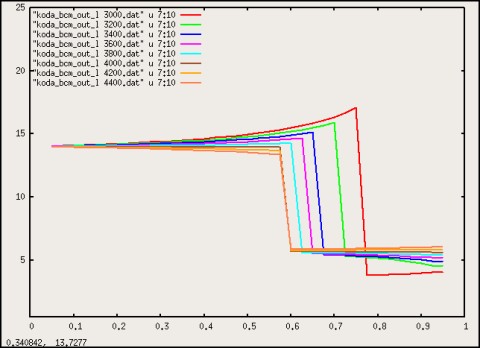
|
Figure 4: Transition density $\eta(l_{2},X)$ for $l_{2}$ in the range
$3.0 - 4.4$.
|
|
Figure 5: As in Fig 4 but for the smectic period $\lambda$.
|
So:
it seems that a change of sign for the indicator $-s11/s12$ is not
necessarily resulting in a demixed S2 phase. At least, if there is such
a transition it is only gradual.
Spherocylinders, mixed:
Of course, we can play that game also with capped cylinders.
Let $l_{1},l_{2}$ again be the lengths of the longer and shorter cylinders, and
$d_{1},d_{2}$
the respective diameters; the total particle lengths are then $L_{i}=l_{i}+d_{i}$.
Fixing the total length $L_{1}=10$, $d_{1}=d_{2}=1$ we may scan the remaining
2d parameter space $[L_{2,}X]$ for smectic and/or smectically
smectically demixed (S2) states.
In Figure 6 all possible S2 states are indicated by a $z$ value of 1 while for
S1 and N states $z=0$.

|
|
Figure 6: "Phase surface" of the $L_{1}=10$, $d_{1}=d_{2}=1$
SPC system.
|
Again, let us concentrate on the vicinity of $L_{2}=4$.
Both $\eta (L_{2},X) $ (Fig. 7) and $\lambda (L_{2},X) $ (Fig. 8) show no
discontinuities here. (The behaviour of $\lambda$ at small $L_{2}$ seems to indicate
that the system wants to demix globally; but as in the BC case this region
should be investigated some more.)
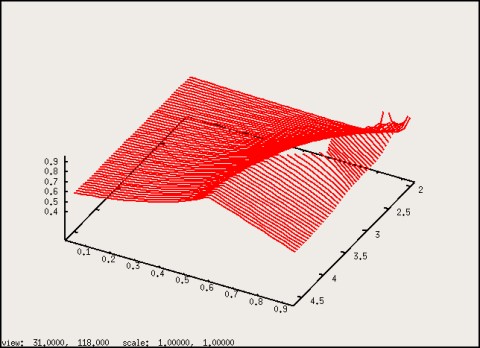
|
|
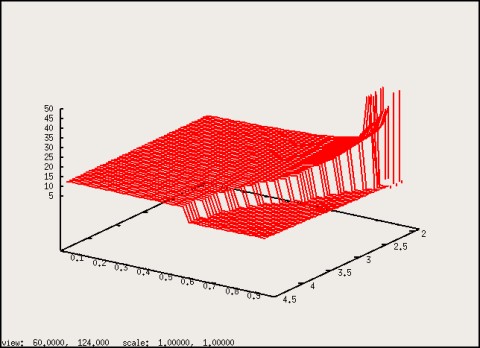
|
Figure 7: Transition density $\eta(L_{2},X)$ for SPC
|
|
Figure 8: Smectic period $\lambda$ as a function of $(l_{2},X)$.
|
Again, some 2D plots are given in Figures 9 and 10.
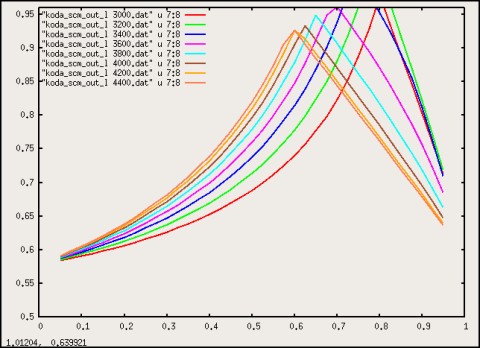
|
|
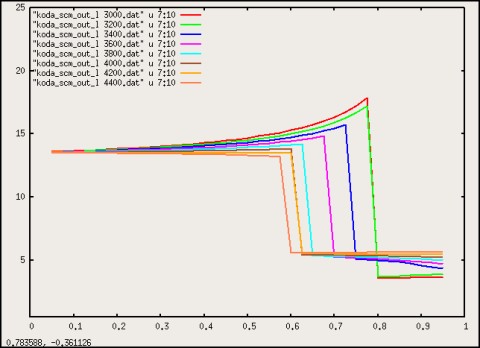
|
Figure 9: Transition density $\eta(L_{2},X)$ for $L_{2}$ in the range
$3.0 - 4.4$.
|
|
Figure 10: As in Fig 9 but for the smectic period $\lambda$.
|
|
vesely jan-2008
|