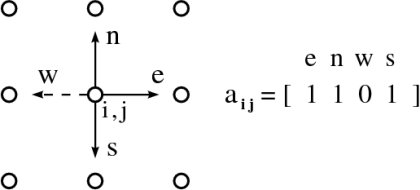| Franz J. Vesely > CompPhys Tutorial > Selected Applications > Hydrodynamics |
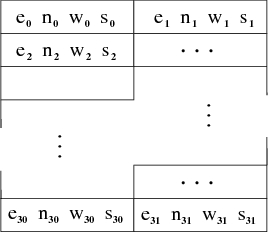
8.3 Lattice Gas Models for Hydrodynamics8.3.1 Lattice Gas Cellular AutomataThe first example of cellular automata was John H. Conway's computer game "Life": some initial pixel patterns on a screen are set, and at each iterative step every pixel is set or erased depending on the status of the neighboring pixels. [Eigen 82]Generally, cellular automata are one- or two-dimensional bit patterns that evolve in (discrete) time according to certain simple rules. They have come to play a role in such diverse fields as informatics [Wolfram 86], evolution theory, and the mathematical theory of complexity [Wolfram 84]. The HPP model A model representing a two-dimensional flow field in terms of bit patterns was introduced by Hardy, Pomeau and de Pazzis. Their "HPP model" is defined as follows [Hardy 73]: -- Represent the flow region by a point lattice -- Populate each grid point $(i,j)$ with up to four "particles" whose velocities must point into different compass directions -- Absolute value of each velocity is always $v=1$ There are $2^{4}=16$ possible "states" of a grid point. Representation: Use a 4-bit (half-byte) computer word $a_{i,j}$ to describe the "empty" or "full" status of the compass directions E,N,W,S by one bit each (see Fig. 8.3.) Alternative representation: Combine the bits referring to the same direction at several successive grid points into one computer word. Example: In a $16 \times 16$ grid each compass direction described by a set of 32 words of 1 byte each (see Fig. 8.4.) Evolution law: $t_{n}$ $\longrightarrow$ $t_{n}$ by a deterministic rule comprised of two substeps, Free flight and Scattering.
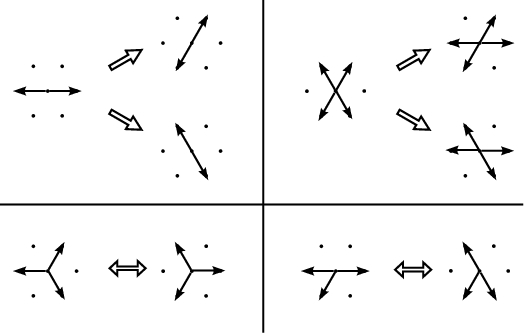
Reviews of the performance of this simple model: [Frisch 86], [Wolfram 86B]. Application: -- Population number at a grid point = density at that position -- Sum of velocities at $(i,j)$ = local velocity density -- Coarse-graining in space and time $\longrightarrow$ averaged dynamics obeys equations similar to the flow equations -- However: only logical operations $\longrightarrow$ calculations are much faster! Improvement: the FHP model Frisch, Hasslacher, and Pomeau [Frisch 86]: suggested to introduce hexagonal cells in place of the simple quadratic lattice: -- Six possible flight directions per grid point -- More scattering rules (see Figure 8.6) Possible refinements of FHP: Possibility of particles at rest $\longrightarrow$ richer microdynamics. Advantage of FHP over HPP: Rotational symmetry of the flow distribution, in spite of the discretized velocities. FHP in 3 dimensions: To retain rotational symmetry, a four-dimensional face centered hypercubic (FCHC) lattice is set up and used in the propagation and collision steps. The results are then mapped onto three dimensions following a rule due to d'Humieres. Note: In the basic HPP and FHP models the particles lose their identity in the process of scattering (see Figs. 8.5 and 8.6.) To determine single particle properties, like velocity autocorrelations, "tag" some particles and pass the tags in the scattering step in a unique way. $\longrightarrow$ Application: Long time behavior of the velocity autocorrelation function [Frenkel, Ernst]. Using a two-dimensional FHP simulation with tagging, Frenkel et al. were able to produce proof for the expected $t^{-1}$ long time tail. 8.3.2 The Lattice Boltzmann MethodProblem with HPP and FHP: Numerical noise $\longrightarrow$ coarse-graining needed to smooth out the results.Reason: at each grid point, each discrete velocity $\vec{c}_{i}$ may be taken by just one or no particle. Improvement: Relax the "zero or one" rule; use a floating point number to describe the degree to which each $(\vec{r},\vec{c})$-cell is filled. $\longrightarrow$ Floating point arithmetic again, but digital noise reduced. Let $f_{i}(\vec{r},t)$ be the density, at time $t$, at position $\vec{r}$ and velocity $\vec{c}_{i}$. Let the velocity vectors point to each of the nearest neighbours on the lattice, with magnitudes such that after one time step ($\Delta t=1$) each particle arrives at that neighbouring site. Example 1: 2D square lattice; 8 neighbour sites, one "rest" status ($i=0$) $\longrightarrow$ 9 numbers $[f_{i}(\vec{r},t)\, , \; i=0,1, \dots 8]$ at each grid point. For speeds, take $|\vec{c}_{0}|=0$, $|\vec{c}_{i}|=1$ along the 4 grid axes, $|\vec{c}_{i}|=\sqrt{2}$ along the 4 diagonal directions. Example 2: 2D hexagonal (FHP) lattice; 6 nearest neighbours, 1 rest particle. Example 3: 3D models; invoke the method introduced by d'Humieres for lattice gas cellular automata (4D FCHC lattice plus down projection.) Procedure: Translation and collision are included in the propagation formula $ f_{i}(\vec{r}+\vec{c}_{i},t+1)= f_{i}(\vec{r},t) + \Delta_{i}(f) $ where $\Delta_{i}(f)$ denotes the increase or decrease of $f_{i}$ due to the collision process. Collision term: Originally, boolean operators were invoked as in the HPP and FHP schemes. Later the LB model was regarded as a representation of the NS equations, independent of the lattice gas model. [Quian 92, Chen 91, 94] $\longrightarrow$ New approximations for the collision term: the single time relaxation expression
$
\Delta_{i}(f)=- \frac{\textstyle f_{i}-f_{i}^{eq}}{\textstyle \tau}
$
was found to be sufficient to reproduce Navier-Stokes dynamics. Here, $1/\tau$ is a relaxation rate, and $f_{i}^{eq}$ denotes an equilibrium distribution. For the 2-D hexagonal lattice this distribution is [Quian 95, Chen 94]
$ \begin{eqnarray}
f_{i=1 \dots 6}^{eq}&=&\frac{\textstyle \rho}{\textstyle 12}
+\frac{\textstyle \rho}{\textstyle 3}\, \vec{e}_{i}\cdot\vec{v}
+\frac{\textstyle 2\rho}{\textstyle 3}\, \left(\vec{e}_{i}\cdot\vec{v}\right)^{2}
-\frac{\textstyle \rho}{\textstyle 6}\, \cdot\vec{v}^{2}
\\
f_{i=0}^{eq}&=&\frac{\textstyle \rho}{\textstyle 2} - \rho \vec{v}^{2}
\end{eqnarray} $
where $\vec{e}_{i}$ is a unit vector along $\vec{c}_{i}$, and $\rho$ and $\vec{v}$ are the hydrodynamic density and flow velocity, respectively:
$
\rho(\vec{r},t) = \sum_{i} f_{i}(\vec{r},t) \;\;\;\;\;
\rho \vec{v}(\vec{r},t) = \sum_{i} \vec{c}_{i}f_{i}(\vec{r},t)
$
Applications of LB: -- Compressible and incompressible flow -- Basic studies of the dynamics of vortices -- Applied studies of turbulent channel flow -- Oil recovery from sandstone -- etc. Surveys of LB: Quian 95 and current synopses on the Web. vesely 2006
|