III. SELECTED APPLICATIONS

Franz J. Vesely > CompPhys Tutorial > Selected Applications > Hydrodynamics

Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

Part III: Ch. 8

8.1 Compressible Flow without Viscosity

Example: Frictionless air flow in the vicinity of an aircraft.

The flow equations in Eulerian formulation reduce to

$ \begin{eqnarray} \frac{\textstyle \partial \rho }{\textstyle \partial t}+ \nabla \cdot \rho \vec{v} &=& 0 \\ \frac{\textstyle \partial \rho \vec{v}}{\textstyle \partial t}+ \nabla \cdot \left[ \rho \vec{v} \vec{v} \right] + \nabla p &=& 0 \\ \frac{\textstyle \partial e}{\textstyle \partial t}+ \nabla \cdot \left[ (e+p) \vec{v} \right]&=&0 \end{eqnarray} $ (8.5-8.7)

Euler derivative: laboratory-fixed coordinate system; $\partial / \partial t$ at a fixed point in space

Lagrange derivative: properties of a volume element that is moving along with the flow; $ d /dt \equiv \partial / \partial t + \vec{v} \cdot \nabla $

$\longrightarrow$ Lagrange form of the flow equations:

$ \begin{eqnarray} \frac{\textstyle d \rho}{\textstyle dt} &=& - \rho \nabla \cdot \vec{v} \\ \rho \frac{\textstyle d \vec{v}}{\textstyle dt} &=& - \nabla p \\ \frac{\textstyle d e}{\textstyle dt} &=& - (e+p) \nabla p -(\vec{v} \cdot \nabla)\, p \\ &=& -e (\nabla \cdot \vec{v}) - \nabla \cdot (p \vec{v}) \end{eqnarray} $ (8.8-8.10)

where the last equation may be written (see 8.4),

$ \frac{\textstyle d \epsilon}{\textstyle dt} = - \, \frac{\textstyle p}{\textstyle \rho} \,(\nabla \cdot \vec{v}) $ (8.11)

8.1.1 Explicit Eulerian Methods

Rewrite Euler's equations as

$ \frac{\textstyle \partial \vec{u}}{\textstyle \partial t}= -\frac{\textstyle \partial \vec{j}_{x}}{\textstyle \partial x} -\frac{\textstyle \partial \vec{j}_{y}}{\textstyle \partial y} -\frac{\textstyle \partial \vec{j}_{z}}{\textstyle \partial z} $ (8.12)

where

$ \vec{u}=\left( \begin{array}{c}\rho \\ \rho v_{x} \\ \rho v_{y} \\ \rho v_{z} \\ e \end{array} \right)\;,\;\; \vec{j}_{x}=\left( \begin{array}{c}\rho v_{x}
\rho v_{x}^{2}+p \\ \rho v_{y}v_{x} \\ \rho v_{z}v_{x} \\ (e+p)v_{x} \end{array} \right)\;,\;\; \vec{j}_{y}=\left( \begin{array}{c}\rho v_{y} \\ \rho v_{x}v_{y} \\ \rho v_{y}^{2}+p \\ \rho v_{z}v_{y} \\ (e+p)v_{y} \end{array} \right)\;,\;\; \vec{j}_{z}=\left( \begin{array}{c}\rho v_{z} \\ \rho v_{x}v_{z} \\ \rho v_{y}v_{z} \\ \rho v_{z}^{2}+p \\ (e+p)v_{z} \end{array} \right) $ (8.13)
Apply any of the methods for conservative-advective (hyperbolic) equations -- Lax, Lax-Wendroff, leapfrog.

Example: 1D Euler / Lax

$ \begin{eqnarray} \rho_{j}^{n+1}&=&\frac{\textstyle 1}{\textstyle 2}\left(\rho_{j+1}^{n}+\rho_{j-1}^{n} \right) -\frac{\textstyle \Delta t}{\textstyle 2 \Delta x} \left(\rho_{j+1}^{n} v_{j+1}^{n}-\rho_{j-1}^{n}v_{j-1}^{n} \right) \\ \rho_{j}^{n+1}v_{j}^{n+1}&=&\frac{\textstyle 1}{\textstyle 2} \left(\rho_{j+1}^{n}v_{j+1}^{n}+\rho_{j-1}^{n}v_{j-1}^{n}\right) -\frac{\textstyle \Delta t}{\textstyle 2 \Delta x} \left[\rho_{j+1}^{n}(v_{j+1}^{n})^{2}+p_{j+1}^{n} -\rho_{j-1}^{n}(v_{j-1}^{n})^{2}-p_{j-1}^{n} \right] \\ e_{j}^{n+1}&=&\frac{\textstyle 1}{\textstyle 2}\left(e_{j+1}^{n}-e_{j-1}^{n} \right) -\frac{\textstyle \Delta t}{\textstyle 2 \Delta x} \left[ \left(e_{j+1}^{n}+p_{j+1}^{n}\right)v_{j+1}^{n} -\left(e_{j-1}^{n}+p_{j-1}^{n}\right)v_{j-1}^{n} \right] \end{eqnarray} $ (8.14-8.16)

8.1.2 Particle-in-Cell Method (PIC)

Consider an ideal gas; assume adiabatic equation of state (fast flow or slow conduction of heat): $p/\rho^{\gamma}= c$ constant in a flowing element $\longrightarrow$ Lagrangian time derivative $\partial c / \partial t + \vec{v} \cdot \nabla c = 0$. Therefore

$ \frac{\textstyle \partial }{\textstyle \partial t} \left[ \rho c \right]+ \nabla \cdot \left[ \rho c \vec{v} \right] = 0 $ (8.17)

(continuity equation for $c$).
$\longrightarrow$ Flow equations:

$ \begin{eqnarray} \frac{\textstyle \partial \rho }{\textstyle \partial t}+ \nabla \cdot \left( \rho \vec{v} \right) &=& 0 \\ \frac{\textstyle \partial \rho \vec{v}}{\textstyle \partial t}+ \nabla \cdot \left( \rho \vec{v} \vec{v} \right) &=& -\nabla p \\ \frac{\textstyle \partial }{\textstyle \partial t} \left( \rho c \right) + \nabla \cdot \left( \rho c \vec{v} \right) &=& 0 \end{eqnarray} $ (8.18-20)

Strategy:

Discretize the time: $t_{n+1} \equiv t_{n}+\Delta t$
Assume a 2D (or 3D) Euler lattice with $\Delta x=\Delta y= \Delta l$
Represent the (variable) local density by a number of particles in each cell
Each particle $k$ represents a fluid element (not a molecule!) and carries a vector of properties,

$ \vec{u}_{k}^{n} \equiv \vec{u}_{k}(t_{n}) \equiv \left\{ \vec{r}_{k}^{n}, \vec{v}_{k}^{n}, c_{k}^{n} \right\} \;\;\; k=1, \dots N $    (8.21)

The properties of the Eulerian (space fixed) cells $(i,j)$ are sums over the particles they contain:

$ \begin{eqnarray} \rho_{i,j}^{n}&=&\frac{\textstyle m}{\textstyle (\Delta l)^{2}} \sum \limits_{k=1}^{N} \, \delta \left[ \vec{r}_{k}^{n}(i,j) \right] \\ (\rho \vec{v})_{i,j}^{n}&=&\frac{\textstyle m}{\textstyle (\Delta l)^{2}} \sum \limits_{k=1}^{N} \, \vec{v}_{k}^{n} \delta \left[ \vec{r}_{k}^{n}(i,j) \right] \\ (\rho c)_{i,j}^{n}&=&\frac{\textstyle m}{\textstyle (\Delta l)^{2}} \sum \limits_{k=1}^{N} \, c_{k}^{n}\delta \left[ \vec{r}_{k}^{n}(i,j) \right] \end{eqnarray} $    (8.22-8.24)

with

$ \delta \left[ \vec{r}(i,j) \right] \equiv \delta \left[ \mbox{int}(\frac{\textstyle x}{\textstyle \Delta l})-i \right] \delta \left[ \mbox{int}(\frac{\textstyle y}{\textstyle \Delta l})-j \right] $    (8.25)
Now rewrite (8.19) as

$ \rho \frac{\textstyle \partial \vec{v}}{\textstyle \partial t} = - \nabla p - \vec{v} \frac{\textstyle \partial \rho}{\textstyle \partial t} - \nabla \cdot \left( \rho \vec{v} \vec{v} \right) $ (8.26)

and first treat only the part $\rho \partial \vec{v} / \partial t = - \nabla p$:

$ \begin{eqnarray} v_{x,i,j}^{n+1} &=& v_{x,i,j}^{n} - a \left( p_{i+1,j}^{n}- p_{i-1,j}^{n} \right) \\ v_{y,i,j}^{n+1} &=& v_{y,i,j}^{n} - a \left( p_{i,j+1}^{n}- p_{i,j-1}^{n} \right) \end{eqnarray} $ (8.27-8.28)

with $a \equiv \Delta t \left/ 2 (\Delta l) \rho_{i,j}^{n} \right.$
Update the particle properties $\vec{v}_{k}$ and $c_{k}$, thus:

$ \vec{v}_{k}^{n+1} = \vec{v}_{i,j}^{n+1} \quad {\rm and} \quad c_{k}^{n+1}=p_{i,j}^{n}/(\rho_{i,j}^{n})^{\gamma} $ (8.29)
Now treat the Lagrangian part of equation 8.26, by letting the fluid particles move with appropriate velocities: Defining

$ \vec{v}_{i,j}^{n+1/2} = \frac{\textstyle 1}{\textstyle 2} \left[ \vec{v}_{i,j}^{n+1} + \vec{v}_{i,j}^{n} \right] $ (8.30)

compute the particle velocities as a weighted sum over the adjacent Eulerian cells:

$ \vec{v}_{k}^{n+1/2}= \frac{\textstyle 1}{\textstyle (\Delta l)^{2}} \sum \limits_{(ij)} a_{(ij)} \vec{v}_{(ij)}^{n+1/2} $ (8.31)

where the weights $a_{(ij)}$ are the overlap areas of a square of side length $\Delta l$ centered around particle $k\,$ and the nearest Euler cells $(ij)$. (See the
particle-mesh method of Section 6.5.2; see Fig. 6.9.)
Update the positions

$ \vec{r}_{k}^{n+1}=\vec{r}_{k}^{n} + \Delta t \,\vec{v}_{k}^{n+1/2} $ (8.32)

to complete the time step.

Here is the procedure in concise form:

PIC method (2-dimensional): At time $t_{n}$ the state of the fluid is represented by $N$ particles with the property vectors $\vec{u}_{k}^{n} \equiv \left\{ \vec{r}_{k}^{n},\vec{v}_{k}^{n}, c_{k}^{n} \right\} \;$ ($k=1,\dots N$). In each Eulerian cell of side length $\Delta l$ there should be at least $\approx 100$ particles.

Compute, for each Euler cell $(i,j)$, the cell properties

$ \begin{eqnarray} \rho_{i,j}^{n}&=&\frac{\textstyle m}{\textstyle (\Delta l)^{2}} \sum\limits_{k=1}^{N} \, \delta \left[ \vec{r}_{k}^{n}(i,j) \right] \\ (\rho \vec{v})_{i,j}^{n}&=&\frac{\textstyle m}{\textstyle (\Delta l)^{2}} \sum\limits_{k=1}^{N} \, \vec{v}_{k}^{n} \delta \left[ \vec{r}_{k}^{n}(i,j) \right] \\ (\rho c)_{i,j}^{n}&=&\frac{\textstyle m}{\textstyle (\Delta l)^{2}} \sum\limits_{k=1}^{N} \, c_{k}^{n}\delta \left[ \vec{r}_{k}^{n}(i,j) \right] \end{eqnarray} $
Using the equation of state to evaluate cell pressures $p_{i,j}$, compute new (preliminary) flow velocities according to

$ \begin{eqnarray} v_{x,i,j}^{n+1} &=& v_{x,i,j}^{n} - a \left( p_{i+1,j}^{n}- p_{i-1,j}^{n} \right) \\ v_{y,i,j}^{n+1} &=& v_{y,i,j}^{n} - a \left( p_{i,j+1}^{n}- p_{i,j-1}^{n} \right) \end{eqnarray} $

with $ a \equiv \Delta t \left/ 2 (\Delta l) \rho_{i,j}^{n} \right.$. For each fluid particle $k$ we now have $\vec{v}_{k}^{n+1}=\vec{v}_{i,j}^{n+1}$ and $c_{k}^{n+1}=p_{i,j}^{n}/(\rho_{i,j}^{n})^{\gamma}$.
From the time-centered cell velocities $\vec{v}_{i,j}^{n+1/2} \equiv$ $\left[ \vec{v}_{i,j}^{n+1} + \vec{v}_{i,j}^{n} \left. \right] \right/ 2 \;$, compute for each particle $k$ an intermediate velocity

$ \vec{v}_{k}^{n+1/2}= \frac{\textstyle 1}{\textstyle (\Delta l)^{2}} \sum \limits_{(ij)} a_{(ij)} \vec{v}_{(ij)}^{n+1/2} $

using suitable weights $a_{(ij)}$ (see text); calculate new particle positions

$ \vec{r}_{k}^{n+1}=\vec{r}_{k}^{n} + \Delta t \,\vec{v}_{k}^{n+1/2} $
Each particle is now given the new state vector

$ \vec{u}_{k}^{n+1} \equiv \left\{ \vec{r}_{k}^{n+1}, \vec{v}_{k}^{n+1}, c_{k}^{n+1} \right\} $

Particle-in-cell method. Note that pressure gradients are evaluated using an Eulerian grid, while the transport of mass, momentum and energy is treated in continuous space.

8.1.3 Smoothed Particle Hydrodynamics (SPH)

Motivation:
PIC technique uses both Eulerian and Lagrangian elements. Average density within a cell = number of point particles in that cell.
Can we represent the local fluid density without a grid?
Lucy and Gingold & Monaghan: load each particle with a spatially extended interpolation kernel $\longrightarrow$ Average local density = sum over the individual contributions.
Let $w(\vec{r}-\vec{r_{i}})$ denote the interpolation kernel centered around $\vec{r_{i}}$. Then the local density at $\vec{r}$ is

$ \langle \rho(\vec{r})\rangle = \sum \limits_{i=1}^{N} m_{i}\, w(\vec{r}-\vec{r_{i}}) $ (8.33)

Generally, a property $A(\vec{r})$ is represented by its "smoothed particle estimate"

$ \langle A(\vec{r})\rangle = \sum \limits_{i=1}^{N} m_{i}\, \frac{\textstyle A(\vec{r}_{i})}{\textstyle \rho(\vec{r}_{i})} \, w(\vec{r}-\vec{r_{i}}) $ (8.34)

Form of the interpolation kernel: Gaussian or polynomial
Example:

$ w(\vec{s}) = \frac{\textstyle 1}{\textstyle \pi^{3/2}d^{3}} \, e^{\textstyle - s^{2}/d^{2}} $ (8.35)

with a width $d$ chosen such that the number of particles within $d$ is $N \approx 5$ in 2 dimensions and $N \approx 15$ for 3 dimensions.
Now rewrite the Lagrangian equations of motion 8.8-8.11 in smoothed particle form.

Note: In the momentum equation $d \vec{v}/dt=- \nabla p / \rho$, interpolating $\rho$ and $\nabla p$ directly would not conserve linear and angular momentum [Monaghan].
$\longrightarrow$ Use the identity

$ \frac{\textstyle 1}{\textstyle \rho}\, \nabla p = \nabla \left( \frac{\textstyle p}{\textstyle \rho}\right) + \frac{\textstyle p}{\textstyle \rho^{2}}\, \nabla \rho $ (8.36)

and the SPH expressions for $A \equiv p/\rho $ and $A \equiv \rho$ to find

$ \frac{\textstyle d \vec{v}_{i}}{\textstyle dt} = - \sum \limits_{k=1}^{N}m_{k} \left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} + \frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} \right) \, \nabla_{i}w_{ik} $ (8.37)

with $w_{ik} \equiv w(\vec{r}_{ik}) \equiv w(\vec{r}_{k}-\vec{r}_{i})$. If $w_{ik}$ is Gaussian, this equation describes the motion of particle $i$ under the influence of central pair forces

$ \vec{F}_{ik}=-m_{i}m_{k}\left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} + \frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} \right) \frac{\textstyle 2 \vec{r}_{ik}}{\textstyle d^{2}}w_{ik} $ (8.38)

The SPH equivalents of the other Lagrangian flow equations are

$ \frac{\textstyle d \rho_{i}}{\textstyle dt} = \sum \limits_{k=1}^{N}m_{k}\, \vec{v}_{ik} \cdot \nabla_{i}w_{ik} $ (8.39)

where $\vec{v}_{ik} \equiv \vec{v}_{k}-\vec{v}_{i}$, and

$ \frac{\textstyle d \epsilon_{i}}{\textstyle dt} = - \frac{\textstyle 1}{\textstyle 2} \sum \limits_{k=1}^{N}m_{k}\, \left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} + \frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} \right) \, \vec{v}_{ik} \cdot \nabla_{i}w_{ik} $ (8.40)

Note: The density equation need not be integrated; just update all positions $\vec{r}_{i}$, then invoke equ. 8.33 to find $\rho(\vec{r}_{i})$. To update $\vec{r}_{i}$ the obvious relation

$ \frac{\textstyle d \vec{r}_{i}}{\textstyle dt} = \vec{v}_{i} $ (8.41)

might be used; a better way is

$ \frac{\textstyle d \vec{r}_{i}}{\textstyle dt} = \vec{v}_{i} + \sum \limits_{k=1}^{N} \frac{\textstyle m_{k}}{\textstyle \bar{\rho}_{ik}} \vec{v}_{ik}\,w_{ik} $ (8.42)

with $\bar
{\rho}_{ik} \equiv (\rho_{i}+\rho_{k})/2$. This relation maintains angular and linear momentum conservation, with the additional advantage that nearby particles will have similar velocities [Monaghan 89].

To solve equs. 8.39, 8.37, 8.41, and 8.40, use any suitable algorithm (see Chapter 4.) Popular schemes are the leapfrog algorithm, predictor-corrector and Runge-Kutta methods.

Example: Variant of the half-step technique [Monaghan 89]:
Given all particle positions at time $t_{n}$, the local density at $\vec{r}_{i}$ is computed from 8.39. Writing equs. 8.37 and 8.40 as

$ \frac{\textstyle d\vec{v}_{i}}{\textstyle dt} = \vec{F}_{i} \;\;\;\;
{\rm and} \;\;\; \frac{\textstyle d\epsilon_{i}}{\textstyle dt} = Q_{i} $ (8.43)

compute the predictors

$ \vec{v}_{i}^{n+1}=\vec{v}_{i}^{n}+\Delta t \, \vec{F}_{i}^{n} \, , \; \; \; \epsilon_{i}^{n+1}=\epsilon_{i}^{n}+\Delta t \, Q_{i}^{n} $ (8.44)

and

$ \vec{r}_{i}^{n+1}=\vec{r}_{i}^{n}+\Delta t \, \vec{v}_{i}^{n} $ (8.45)

Determine mid-point values of $\vec{r}_{i}$, $\vec{v}_{i}$ and $\epsilon_{i}$ according to

$ \vec{r}_{i}^{n+1/2} = \left( \vec{r}_{i}^{n}+\vec{r}_{i}^{n+1}\right) /2 $ (8.46)

etc. From these, compute mid-point values of $\rho_{i}$, $\vec{F}_{i}$ and $Q_{i}$ and insert these in correctors of the type

$ \vec{v}_{i}^{n+1}=\vec{v}_{i}^{n}+\Delta t \, \vec{F}_{i}^{n+1/2} $ (8.47)

Here is an overview of the SPH method:

Smoothed particle hydrodynamics: At time $t_{n}$ the state of the fluid is represented by $N$ particles with masses $m_{i}$ and the property vectors

$\vec{u}_{i}^{n} \equiv \left\{ \vec{r}_{i}^{n}, \vec{v}_{i}^{n}, \epsilon_{i}^{n} \right\}\;$

$(i=1, \dots N)$. In the simple case of an ideal gas undergoing adiabatic flow, the specific energy $\epsilon$ may be replaced by $c \equiv p/\rho^{\gamma}$ $= \epsilon (\gamma -1)/\rho^{\gamma - 1} \,$. A suitable interpolation kernel is assumed, e.g. $ w(\vec{s}) = (1/\pi^{3/2}d^{3}) exp\{- s^{2}/d^{2}\}$, with the width $d$ chosen so as to span about 5 (in 2 dimensions) or 15 (3-d) neighbors.

At each particle position $\vec{r}_{i}$ the density $\rho_{i}$ is computed by interpolation:

$ \rho_{i} = \sum \limits_{k=1}^{N} m_{k}\, w(\vec{r}_{ik}) $
From the given equation of state $p=p(\rho, \epsilon)$ compute the pressures $p_{i} = p(\rho_{i},\epsilon_{i})$.
Integrate the equations of motion

$ \begin{eqnarray} \frac{\textstyle d \vec{r}_{i}}{\textstyle dt} &=& \vec{v}_{i} \; \;\; {\rm (or \;\;\;equ. \;\;\; 8.42)} \\ \frac{\textstyle d \vec{v}_{i}}{\textstyle dt} &=& - \sum \limits_{k=1}^{N}m_{k} \left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} + \frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} \right) \, \nabla_{i}w_{ik} \\ \frac{\textstyle d \epsilon_{i}}{\textstyle dt} &=& - \frac{\textstyle 1}{\textstyle 2} \sum \limits_{k=1}^{N}m_{k}\, \left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} + \frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} \right) \, \vec{v}_{ik} \cdot \nabla_{i}w_{ik} \end{eqnarray} $

over one time step by some suitable integrator (Runge-Kutta, or the simple procedure 8.43 - 8.47 ) to obtain

$ \vec{u}_{i}^{n+1} \equiv \left\{ \vec{r}_{i}^{n+1}, \vec{v}_{i}^{n+1}, \epsilon_{i}^{n+1} \right\} \;\;\; i=1, \dots N $

A modification of this scheme is obtained by including the density $\rho_{i}$ in the state vector of particle $i$ and integrating the pertinent equation of motion, 8.39. The time step integrations for $\vec{r}$, $\vec{v}$, $\rho$ and $\epsilon$ may then be performed simultaneously, and the evaluation of the density according to the SPH averaging prescription is omitted. This procedure works faster, but exact mass conservation is not guaranteed.

Note: SPH is not restricted to compressible inviscid flow. Incompressibility may be introduced by using an equation of state that keeps compressibility below a few percent [Monaghan], and viscosity is added by an additional term in the equations of motions for momentum and energy, equs. 8.37 and 8.40:

$ \begin{eqnarray} \frac{\textstyle d \vec{v}_{i}}{\textstyle dt} &=& - \sum \limits_{k=1}^{N} m_{k} \left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} + \frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} + \Pi_{ik} \right) \, \nabla_{i}w_{ik} \\ \frac{\textstyle d \epsilon_{i}}{\textstyle dt} &=& - \sum \limits_{k=1}^{N}m_{k}\, \left( \frac{\textstyle p_{k}}{\textstyle \rho_{k}^{2}} + \frac{\textstyle p_{i}}{\textstyle \rho_{i}^{2}} + \Pi_{ik} \right) \, \vec{v}_{ik} \cdot \nabla_{i}w_{ik} \end{eqnarray} $ (8.48-8.49)

The artificial viscosity term $\Pi_{ik}$ is modeled in the following way:

$ \Pi_{ik} = \left\{ \begin{array}{ll} \begin{array}{c} \underline{ - \alpha \bar{c}_{ik}\mu_{ik}+\beta \mu_{ik}^{2} } \\ \bar{\rho}_{ik}^{} \end{array} & {\rm if }\; \vec{v}_{ik} \cdot \vec{r}_{ik} < 0 \\ 0 & {\rm if}\; \vec{v}_{ik} \cdot \vec{r}_{ik} \geq 0 \end{array} \right. $ (8.50)

where $c$ is the speed of sound, $\mu$ is defined by

$ \mu_{ik} \equiv \frac{\textstyle ( \vec{v}_{ik} \cdot \vec{r}_{ik}) \, d}{\textstyle r_{ik}^{2}+ \eta^{2}} $ (8.51)

and $c_{ik} \equiv c_{k}- c_{i}$ and $\bar{c}_{ik} \equiv (c_{i}+c_{k})/2$ etc.
This form of $\Pi$ introduces the effects of shear and bulk viscosity. The parameters $\alpha$ and $\beta$ should be near $\alpha = 1$ and $\beta = 2$ for best results [Monaghan]. The quantity $\eta$ prevents singularities for $r_{ik} \approx 0$. It should be chosen such that $\eta^{2}=0.01 d^{2}$.

Additional features:

Thermal conduction may be included. See [Monaghan 89].

Interfaces: Introduce dummy particles on the far side of the boundary. By picking the properties of these particles appropriately one can mimick a free surface or a "sticky" solid boundary. See Nugent and Posch [Nugent] for free surfaces, and [Ivanov]: for rough interfaces.

Sample application: "Rayleigh-Bénard" convection
A fluid layer is heated carefully from below and cooled from above. $\longrightarrow$ Formation of stable convective rolls transporting heat from the bottom to the top. See the Figure for a match between SPH and an Euler-type calculation [Hoover 99]:
- Computing times comparable for both calculations
- Results are in good agreement
- Fluctuations in SPH (like in any particle-type calculation), none in Euler
- SPH code is quite simple -- similar to an MD program; Euler code very massive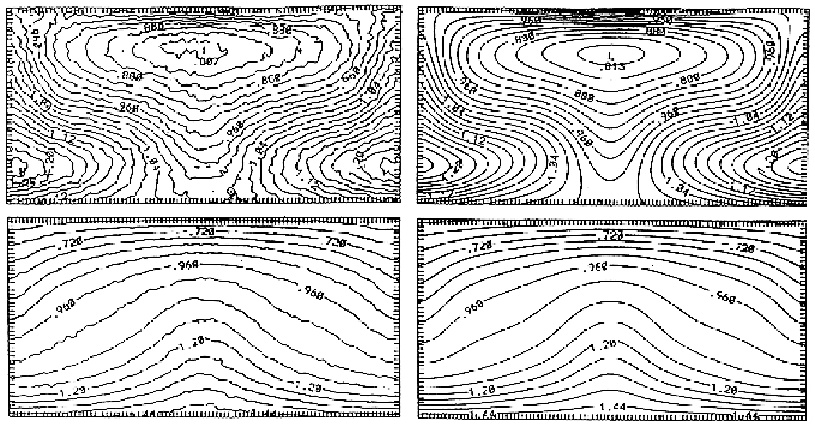

Figure: Comparison of Smoothed Particle Hydrodynamics with an Eulerian finite-difference calculation. The density (above) and temperature (below) contours for a stationary Rayleigh-Bénard flow are shown. Left: SPH; right: Euler. (From [Hoover 99], with kind permission by the author)

vesely 2006