| Franz J. Vesely > CompPhys Tutorial > 2 Linear Algebra |
2.[cgm] Conjugate Gradient MethodActually an exact method, but a multi-step approach.Task: Solve $ A \cdot x = b$. This may be interpreted as a minimization problem: Let Then the $N$-vector $x$ which minimizes $f(x)$ (with the minimum value $f=0$) is the desired solution. Minimization of a quadratic function of $N$ variables:
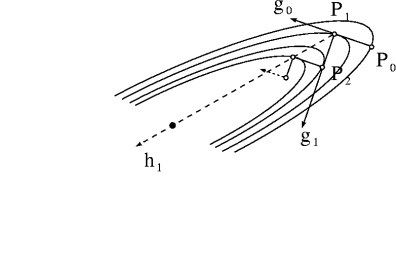
Warm-up: Cauchy's Steepest Descent Method Assume $f$ to depend on two variables $\vec{x}=(x_{1},x_{2})$ only. The lines of equal elevation of a quadratic function are ellipses that may be very elongated (see the figure).
Now for the serious work: Conjugate Gradients From point $P_{1}$ take the direction $\vec{h}_{1}$ instead of $\vec{g}_{1}$. BUT: How to find $\vec{h}_{1}$? Require that along $\vec{h}_{1}$ the change of the gradient of $f$ has no component parallel to $\vec{g}_{0}$. (In contrast: along $\vec{g}_{1}$, the gradient of $f$ has initially no $\vec{g}_{0}$ -component). As a consequence, a gradient in the direction of $\vec{g}_{0}$ will not develop immediately (on quadratic surfaces never!). $\Longrightarrow$ This requirement leads to the following prescription.
For dimension $N=2$ this is all there is; $\vec{x} = \vec{x}_{2}$ is already the solution vector. For systems of higher dimension one has to go on from $\vec{x}_{2}$ in the direction
\vec{h}_{2} = \vec{g}_{2}
- \frac{\textstyle (A \cdot \vec{g}_{2}) \cdot (A \cdot \vec{h}_{1})}{\textstyle \left| A \cdot \vec{h}_{1} \right|^{2}}
\, .
until the next "low point" is reached at
\vec{x}_{3} = \vec{x}_{2} + \lambda_{3} \, \vec{h}_{2} \, ,
with
\lambda_{3} = \frac{\textstyle \left| \vec{g}_{2} \cdot \vec{h}_{2} \right|}{\textstyle \left| A \cdot \vec{h}_{2} \right|^{2}} \, .
Next we determine $\vec{x}_{4}$ and so forth, until we arrive at the solution $\vec{x} = \vec{x}_{N}$. Advantage of CG: No matrix inversion! But: Several multiplications $A \cdot \vec{x}$; therefore most efficient for sparse matrices. EXAMPLE: To see the mechanics of the method, assume
A=\left( \begin{array}{cc}3&1\\ \\2&4\end{array} \right)
\, ; \;
\vec{b}=\left( \begin{array}{r} 3 \\ \\2 \end{array} \right)
\, ; \;\;
and
\; \; \vec{x}_{0} = \left( \begin{array}{r} 1.2 \\ \\0.2 \end{array} \right)
The gradient vector at $\vec{x}_{0}$ is
\vec{g}_{0} = - A^{T} \cdot \left[ A \cdot \vec{x}_{0} - \vec{b}\right]
= - \left( \begin{array}{r} 4.8 \\ \\5.6 \end{array} \right)
and
\lambda_{1} = \frac{\textstyle \left| \vec{g}_{0} \right|^{2}}{\textstyle \left| A \cdot \vec{g}_{0} \right|^{2}} = 0.038
such that
\vec{x}_{1}=\vec{x}_{0}+\lambda_{1}\vec{g}_{0}=\left( \begin{array}{r} 1.017 \\ \\-0.014 \end{array} \right)
Similarly,
\vec{g}_{1}=\left( \begin{array}{r} -0.063 \\ \\0.054 \end{array} \right) \, , \;\;
\vec{h}_{1}=\left( \begin{array}{r} -0.0635 \\ \\0.0532 \end{array} \right) \, , \;\;
\lambda_{2}=0.262 \, ,
and thus
\vec{x}_{2}= \left( \begin{array}{r} 1.000 \\ \\0.000 \end{array} \right)
which is the desired solution vector in this 2-dimensional case. If $ A$ were a $N \times N$ matrix, $N$ such steps would be necessary. vesely 2005-10-10
|