|
Es handelt sich um eine Zerfallsreihe. Die erste Substanz zerfällt in die zweite, und die zweite hat eine größere Halbwertszeit als die erste. Dadurch wird zunächst mehr von der zweiten Substanz nachproduziert als zerfallen kann, wodurch ihre Menge ansteigt. Erst wenn die erste Substanz praktisch aufgebraucht ist, macht sich die Abnahme der zweiten bemerkbar. Das zuvor gezeigte Bild zeigt daher keine "Sättigung", sondern nur einen zu kleinen Zeitausschnitt. Über einen längeren Zeitraum betrachtet, sieht der Verlauf so aus: 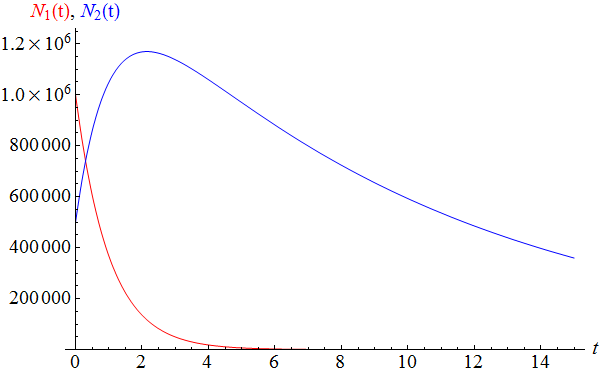 Beschrieben wird dieser Sachverhalt durch ein System von zwei Differentialgleichungen $$\begin{array}{l}{dN_1(t)\over dt}=-\lambda_1 N_1(t)\\ {dN_2(t)\over dt}=\lambda_1 N_1(t)-\lambda_2 N_2(t)\end{array}$$ Dabei sind $\lambda_1$ und $\lambda_2$ die Zerfallskonstanten. Die Halbwertszeiten sind $\tau_1={{\rm ln}\,2\over \lambda_1}$ und $\tau_2={{\rm ln}\,2\over \lambda_2}$. Die allgemeine Lösung ist $$\begin{array}{l}N_1(t)=N_1(0)\,e^{-\lambda_1 t}\\ N_2(t)=N_2(0)\,e^{-\lambda_2 t}+{\lambda_1\over \lambda_1-\lambda_2}N_1(0)\left(e^{-\lambda_2 t}-e^{-\lambda_1 t}\right)\end{array}$$ Für $\lambda_1=\lambda_2\equiv\lambda$ geht sie über in $$\begin{array}{l}N_1(t)=N_1(0)\,e^{-\lambda\,t}\\ N_2(t)=\left(N_2(0)+\lambda\,t N_1(0)\right)\,e^{-\lambda\,t}\end{array}$$ Für die Bilder wurde gewählt: $\lambda_1=1$, $\lambda_2=0.1$, $N_1(0)=10^6$ und $N_2(0)=0.5\cdot 10^6$. Damit ergibt sich $$N_2(t)={5\over 9}\,10^5\,\left(29\,e^{-t/10}-20\,e^{-t}\right)$$ Untersuchen Sie diese Funktion selbst! Als Ergebnis sollten Sie erhalten, dass $N_2(t)$ bis zur Zeit $$t_{\sf max}={10\over 9}\,{\rm ln}\left(200\over 29\right)\approx 2.15$$ ansteigt und erst danach abfällt! Zurück |