|
Von Graphen, Genen und dem WWW

Online-Skriptum
Eva, Ursula und Adam
Viel Gescheites,
aber auch viel Unsinn ist seit der "Entdeckung" der "mitochondrialen"
(oder afrikanischen) Eva geschrieben und geglaubt worden. Wir wollen
uns die Angelegenheit hier vom Standpunkt der Mathematik ansehen und
so manches Missverständnis ausräumen. Interessanterweise sind
die genetischen Befunde mit etwas Wahrscheinlichkeitsrechnung nachvollziehbar,
und es ergeben sich daraus Erkenntnisse über die Größe
der Menschheit zu Evas Zeiten und einige grundlegende Mechanismen über
die Entstehung neuer Populationen und Arten.
Ende der achziger
Jahre kam eine neue Methode auf, entwicklungsgeschichtliche Verhältnisse
des modernen Menschen aufzuklären: Mitochondrien -
die "Kraftwerke" der Zellen - haben
zwei besondere Eigenschaften:
- Sie enthalten ringförmige
DNS-Stränge, die (wie auch die DNS des Zellkerns) Bauanleitungen
für die Synthese von Proteinen enthalten.
- Die in dieser DNS gespeicherte
Information ist - im Unterschied zur Zellkern-DNS
- nicht der Vermischung (Rekombination)
durch sexuelle Fortpflanzung unterworfen. Sie wird von der Eizelle
beigesteuert, d.h. ausschließlich von der Mutter auf die Kinder
übertragen.
Jeder DNS-Ring
besteht aus 16 569 Basenpaaren und enthält
einen Bereich von ungefähr 500 Basenpaaren, der nicht für
Proteine kodiert. Wenn in dieser so genannten "Kontrollregion"
durch eine zufällige Mutation ein Basenpaar durch ein anderes ersetzt
wird, so bringt das, soweit
wir heute wissen, weder Vor- noch Nachteile für den Träger
mit sich. (Mutationen in der Kontrollregion sind "selektionsneutral").
Passiert das in der Keimbahn einer Frau, so geht die veränderte
Sequenz an ihre Kindern über. Die Töchter übertragen
sie wiederum an ihre Kinder, usw.
In Wahrheit
ist es etwas komplizierter: Es dauert ungefähr sechs Generationen,
bis sich herausstellt, ob eine zufällige Mutation in der Kontrollregion
eines DNS-Rings in einem Mitochondrium sich durchsetzt
oder untergeht. Die Menschen, die während dieses Zeitraums in
der betrachteten Erblinie geboren werden, tragen Mitochondrien zweierlei
Typs (mit und ohne die Mutation) in ihren Zellen. Der Einfachheit
halber werden wir diese Komplikation aber ignorieren.
Mitochondrien-Mutationen
werden also immer entlang der weiblichen Linie weitergegeben. Während
genügend langer Zeiträume können sich mehrere Mutationen
ansammeln, so dass die Sequenz der Kontrollregion sich an immer mehr
Stellen von der ursprünglichen unterscheidet. Auf ein solches Phänomen
sind wir in einem früheren Abschnitt
bereits gestoßen: hier tickt eine "molekulare Uhr".
Da sich die Bedingungen im Inneren einer Zelle kaum ändern, dürfen
wir einen regelmäßigen Gang dieser Uhr erwarten. Im Durchschnitt
tritt in einer weiblichen Erblinie ungefähr alle 10 000
Jahre eine Mutation der Kontrollregion auf -
eine ideale Mutationsrate, um Verwandtschaftsstrukturen zu untersuchen,
die die Geschichte der letzten hundertfünfzigausend Jahre widerspiegeln
(und, nebenbei bemerkt, etwa zehnmal so groß wie der Mutationsrate
von Zellkern-DNS).
Wer ist nun Eva?
Sie ist in gewisser Weise die "weibliche Antwort" auf die Frage, wo wir modernen
Menschen herkommen. Hat sich unsere Art, Homo sapiens, an verschiedenen
Orten aus lokalen Populationen der früheren Menschenart Homo
erectus entwickelt? Zählt Homo neanderthalensis zu unseren
Ahnen? Die Sequenzierung der Mitochondrien-DNS heutiger Menschen liefert
starke Indizien dafür, dass beides nicht der Fall war. Die größte
bisher gefundene Differenz zwischen den Kontrollregionen in den Mitochondrien
zweier heutiger Menschen beläuft sich auf 14 Unterschiede. Die
aus Neandertalerknochen extrahierte DNS weicht hingegen an 26 Stellen
von der eines durchschnittlichen heutigen Europäers ab -
ein klarer Hinweis darauf, dass sich die Neandertaler-Linie von unserer
getrennt hatte, lange bevor Homo sapiens Afrika verließ,
und dass später keine Vermischung mehr
stattfand. (Ob sie genetisch möglich gewesen wäre,
wissen wir nicht, und falls es sie dennoch gegeben hat, muss sie sehr
selten gewesen sein).
Sehen wir uns nun ein bisschen im Detail an,
was uns die Mitochondrien über unsere Vergangenheit erzählen.
Nehmen wir eine beliebige Gruppe von Menschen, und fragen wir, woher
sie ihre Mitochondrien-DNS haben. Dazu verfolgen wir alle aufsteigenden
mütterlichen Erblinien (Mutter, Großmutter mütterlicherseits,...).
Nach und nach werden sich diese Linien vereinigen, bis sie schließlich
bei einer eindeutig bestimmten Frau zusammenlaufen -
der jüngsten gemeinsamen Vorfahrin, mit der die betrachteten Menschen
durch eine ununterbrochene weibliche Erblinie bunden sind. Sie ist die
jüngste "maternale Vorfahrin", wie der Fachausdruck
dafür lautet. Machen wir das mit einem Geschwisterpaar, so ist
die jüngste maternale Vorfahrin die (gemeinsame) Mutter. Machen
wir das mit der gesamten Menschheit, so ergibt sich ebenfalls eine eindeutig
bestimmte Frau. Das ist Eva. Würden wir den Verwandtschaftsgraphen
der Menschheit bis in die fernste Vergangenheit kennen, so könnten
wir sie problemlos ermitteln. Von
ihr stammen wir alle über eine ununterbrochene maternale Erblinie
ab.
Eva muss zumindest
zwei Töchter gehabt haben (ansonsten wäre sie nicht die jüngste
maternale Vorfahrin). Die Mitochondrien-DNS in den Erblinien, die von
jeder dieser Töcher ausgehen, entwickelten sich fortan getrennt.
Aufgrund der Mutationen, die sich seither in den einzelnen Linien unabhängig
voneinander angesammelt haben, wurde grob anbeschätzt, dass Eva
vor ungefähr 150 000 Jahren gelebt
hat.
| Ursula,
Jasmin, Helena, Lara und Xenia |
Aber nicht nur
Eva, auch andere besondere Frauen ("Clanmütter" oder
Clangründerinnen) sind auszumachen. Während der letzten zehn
Jahre wurde die Mitochondrien-DNS zahlreicher Menschen (vor allem von
Europäern, aber auch von etlichen tausend Menschen aus anderen
Kontinenten) sequenziert und miteinander verglichen. Daraus ergab sich,
dass ungefähr 95% der europäischen "Ureinwohner"
in sieben Gruppen ("maternale Clans") zerfallen. Sie
wurden aus dem Datenmaterial durch aufwendige Computerberechnungen ermittelt.
(Die Hauptschwierigkeit bestand darin, Parallelmutationen, die unabhängig
voneinander an denselben DNS-Stellen auftraten, zu identifizieren).
Von diesen sieben Frauen dürften fast alle Europäer in maternaler
Linie abstammen. Die älteste, Ursula, lebte vor ungefähr
45 000 Jahren, die jüngste, Jasmin,
vor 10 000 Jahren. Jene mit dem größten
Clan ist Helena, die vor 20 000 Jahren
lebte. Innerhalb der Clans gibt es Untergruppen, die sich wiederum auf
spätere (durch Mutationen überlieferte) Verzweigungen beziehen.
Weltweit wurden bisher 33 maternale Clans identifiziert, und alle ihre
Gründerinnen haben Namen bekommen.
Um uns vorzustellen,
wie es dazu kommt, verfolgen wir die maternalen Erblinien der heute
lebenden Menschen (aufsteigend) in die Vergangenheit zurück.
Viele werden sich nach wenigen Generationen vereinigen. Je weiter wir
zurückschreiten, um so kleiner wird ihre Zahl werden, wie hier
schematisch dargestellt:
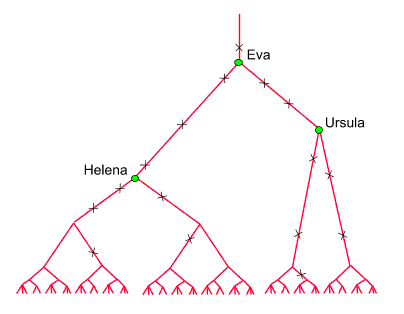
Es werden aber
auch die Punkte, an denen die maternalen Erblinien zusammenlaufen, seltener.
Sie kennzeichnen Frauen, die wirklich gelebt haben. Die ×
Symbole im obigen Dragramm stellen die Mitochondrien-Mutationen dar,
anhand derer diese Frauen (ungefähr) lokalisiert, ihre maternalen
Nachfahren (Clans) bestimmt und ihre Lebenszeiten abgeschätzt werden
können. (Anstelle der bisher identifizierten 33 Clanmütter
haben wir hier nur zwei eingezeichnet. Auch die Abstände entsprechen
nicht den wirklichen Zeiten: Eva und Ursula trennten 5000 Generationen,
während Ursula vor etwas mehr als 2000 Generationen lebte).
So kommen wir durch
rein formale Überlegungen zu dem Schluss: Einige wenige
Frauen stehen an den Punkten, an denen die maternalen Erblinien großer
Gruppen heutiger Menschen zusammenlaufen.
Dabei handelt es
sich keineswegs um nutzlose Spekulationen -
so wurde durch die Analyse von Mitochondrien-DNS die alte Streitfrage
gelöst, ob die Inseln des Pazifik von Asien oder Amerika aus besiedelt
wurden - ersteres war der Fall.
(Genau genommen gelten diese Untersuchungen nur für die weibliche
Erblinie. Nach ihnen wäre es möglich, dass aus Amerika kommende
Männer in den pazifischen Raum eingewandert sind.
Analoge Untersuchungen an Y-Chromosomen, über die wir weiter unten
sprechen werden, lassen aber auch dies als sehr unwahrscheinlich erscheinen).
Auch lässt sich aufgrund dieser Untersuchungen quantifizieren, dass die
Europäer zu etwa 20% von Einwanderern aus dem Nahen Osten, die
(ab etwa 9000 Jahren vor unserer Zeit) die Landwirtschaft mitbrachten,
und zu 80% von einzeitlichen Jägern und Sammlern, die schon lange
zuvor hier wohnten, abstammen. Ein anderer interessanter Punkt, den
die Daten nahelegen, betrifft die Auswanderung von Menschen aus ihrer
afrikanischen Heimat vor ungefähr 100 000
Jahren. Es scheint sich nur einer der 13 afrikanischen Clans (jener,
dessen Begründerin Lara genannt wurde) daran beteiligt haben.
Das spricht dafür, dass es eine sehr kleine Gruppe war, die damals
aufbrach, und von der sich die "Ureinwohner" Eurasiens, Ozeanien
und Amerikas herleiten.
Die Clans decken
sich nicht mit der Einteilung der Menschen in "Stämme",
"Völker" und "Kulturen". So lassen sich beispielsweise
unter den indigenen Einwohnern Amerikas maternale Nachfahren von Xenia
identifizieren, die vor 25 000 Jahren wahrscheinlich
in Europa oder dem westlichen Asien gelebt hat. Alles in allem unterstüzen
die genetischen Daten die Ansicht, dass die Menschheit von Anfang an
eine bunte Mixtur darstellte, die ständig in Bewegung war.
Wie
haben wir uns die "Urmutterschaft" Evas vorzustellen? Hier
drängt sich ein Problem auf: Was ist das Besondere an Eva? Gleichzeitig
mit ihr haben sicher viele andere (hunderte oder tausende) Frauen gelebt
und Kinder bekommen. Wieso sind sie nicht auch "Urmütter"
geworden? Dasselbe Problem tritt auf, wenn wir uns auf die (besser durch
archäologische Funde dokumentierten) Verhältnisse, in denen
die europäischen Clanmütter gelebt haben, beziehen. Welcher
Mechanismus macht Ursula, die vor 45 000
Jahren lebte, zur Clanmutter, währen alle ihre Zeitgenossinnen
(sogar ihre Schwestern) unerwähnt (und unbedankt) bleiben? So,
wie es aussieht, scheinen sie alle nicht im heutigen Mitochondrien-DNS-Befund
auf - zählen sie nicht zu unseren Vorfahren?
Vorschnelle Antwort:
Ihre Nachkommen haben dem einzeitlichen Überlebenskampf nicht standgehalten
und starben schließlich aus? Eine Erklärung dieser Art scheint
in manchen populären Pressemeldungen suggeriert zu werden. Um
herauszufinden, wie es sich wirklich verhält, nehmen wir zunächst
das Vernünftigste an, nämlich dass nichts dergleichen geschehen
ist. Auch Evas (oder Ursulas) Zeitgenossinnen haben Kinder bekommen,
und die meisten dieser Frauen zählen zu unseren Vorfahren. Unsere
(Zellkern-)Gene, die durch die sexuelle Fortpflanzung ständig vermischt
werden, haben wir von diesen frühen Generationen geerbt. Verfolgen
wir die mütterlichen und väterlichen Erblinien der
heutigen Menschen zurück, so nehmen Eva und Ursula keine besonders
privilegierte Stellung ein.
Der entscheidende
Punkt liegt darin, dass Eva und Ursula ihre Stellung der Zurückverfolgung
rein maternaler Erblinien verdanken. Um die Bedeutung dieser
Einschränkung zu vestehen, betrachten wir eine beliebige Zeitgenossin
Evas oder Ursulas, oder irgendeine andere Frau, die irgendwann gelebt
hat - wir nennen sie Alice -
und analysieren die Situation nicht, wie oben, indem wir maternale Linien
zurückverfolgen, sondern von Alices' Standpunkt, indem wir
über ihre Nachkommen Buch führen: Mit welcher Wahrscheinlichkeit
wird Alice eine Clanmutter? Genauer:
Frage: Mit
welcher Wahrscheinlichkeit geht von Alice eine ununterbrochene maternale
Erblinie aus, die bei zumindest einem heute lebenden Menschen endet?
Ist diese Wahrscheinlichkeit sehr klein, so wäre erklärt,
warum Frauen vom Typ Eva und Ursula sehr selten sind.
| Ein
einfaches Modell für Alice |
Da
wir den Verwandtschaftsgraphen der Menschheit nicht kennen, können
wir diese Frage nur im Rahmen vereinfachter Modelle beantworten, aber
wichtig ist das Prinzip, das uns nun zu dieser Antwort führen
wird. Nehmen wir an, jeder Mensch (der ins fortpflanzungsfähige
Alter gelangt) bekäme genau 2
Kinder, die (mit gleicher Wahrscheinlichkeit) eine Tochter
oder ein Sohn sein können, wiederum (je 2)
Kinder bekommen, usw. In diesem Modell stagniert die Bevölkerungszahl,
aber das soll uns nicht stören. Die Population sei lediglich groß
genug, damit sich diese Paarungsarithmetik immer ausgeht.
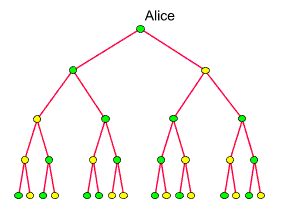
Hier liegt ein
klarer Fall für einen Graphen vor -
genauer: für einen binären Baum, der Alices' Nachkommen darstellt.
Das linke Diagramm zeigt einen solchen Baum:
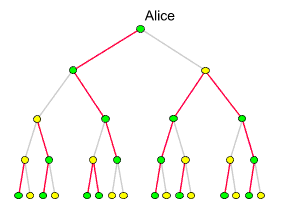
Die Söhne
stiften keine maternalen Erblinien, interessieren uns also nicht weiter.
Daher wird jede Kante, die zu einem Sohn führt, grau eingefärbt.
Das ist im rechten Diagramm dargestellt. Eine maternale Erblinie, ist
ein von Alice absteigender roter Kantenzug
(wobei wir die in Söhnen endenden Kanten nicht mitzählen,
auch wenn sie die Schlusssteine maternaler Erblinien bilden). Wir sehen,
warum Alice in diesem Beispiel bereits eine Generation später
keine Clanmutter mehr ist: Obwohl ihre Nachkommenschaft exponentiell
anwächst, gibt es keine rote Linie,
die bis in die jüngste eingezeichnete Generation reicht. Schon
dieses Diagramm (in dem die Frauen sogar überwiegen) lässt
vermuten, dass lange maternale Erblinien gar nicht so häufig auftreten,
wie man vielleicht intuitiv vermuten würde.
Denken wir uns
einen solchen Baum beliebig weiter fortgesetzt. Jede Kante ist (unabhängig
von allen anderen Kanten) mit gleicher Wahrscheinlichkeit rot oder grau
eingefärbt. (Wir könnten die grauen und alle von ihnen absteigenden
Kanten auch einfach aus dem Graphen entfernen, aber die obige Darstellung
gibt die Situation am klarsten wieder). Ein
solcher Zufallsprozess heißt Galton-Watson-Prozess, und
seine Eigenschaften stellen den Schlüssel für die Lösung
unseres Problems dar: Für jede natürliche Zahl j
ist die Wahrscheinlichkeit, mit der es eine rote
Linie bis in die j-te
Generation gibt (wobei Alice die nullte Generation bildet), wohldefiniert.
Wir bezeichnen sie mit wj .
Es gibt keinen
einfachen geschlossenen Ausdruck für wj,
aber wir können eine Rekursionsformel für diese Größe
herleiten. Die Art, wie wir das machen, ist ein schönes Beispiel
für elegante mathematische Argumentation: Zunächst bemerken
wir, dass von Alices' beiden Kindern je ein Graph ausgeht, der die gleiche
Struktur hat wie der gesamte Baum. Falls Alice eine Tochter hat (wie
im obigen Beispiel), so ist die Wahrscheilichkeit, dass eine rote
Linie von dieser Tochter bis in die j-te
Generation reicht, genau wj-1.
Wir müssen daher nur die drei Möglichkeiten der Geschlechterverteilung
unter Alices Kindern (keine, eine oder zwei Töchter) mit den Wahrscheinlichkeiten,
dass es von den Töchtern aus weitergeht, gewichten. Für die
Fälle keiner und einer Tochter (was mit den Wahrscheinlichkeiten
1/4
und 1/2
auftritt) wissen wir bereits alles nötige. Falls Alice zwei Töchter
hat (was mit der Wahrscheinlichkeit
1/4 auftritt), ist die Wahrscheinlichkeit, dass zumindest
eine von ihnen eine bis in die j-te
Generation reichende rote Linie besitzt,
genau 1 - (1 - wj-1)2
(Gegenwahrscheinlichkeit der Gegenwahrscheinlichkeiten!) Damit ergibt
sich
| wj = (1/4) × 0 + (1/2) × wj-1 + (1/4) × ( 1 - (1 - wj-1)2 ) , |
(1) |
oder, nach
Ausmultiplizieren,
was zusammen mit
dem Anfangswert w0 = 1
eine rekursiv definierte Folge darstellt. Überprüfen wir die
erste Iteration: Als Wahrscheinlichkeit für Alice, eine rote
Linie bis in die erste Generation zu besitzen, ergibt sich w1 = 3/4
(was mit der Wahrscheinlichkeit übereinstimmt, dass Alice mindestens
eine Tochter hat).
Aus (2)
folgt unmittelbar, dass die Folge wj
monoton abnimmt. Da andererseits wj ³ 0
ist, besitzt sie einen Grenzwert, und indem wj
und wj-1
in (2)
durch diesen ersetzt werden, ergibt sich eine quadratische Gleichung,
die nur 0
als Lösung hat. Es handelt sich daher um eine Nullfolge. Um ihr
asymptotisches Verhalten zu bestimmen, setzen wir wj = 1/uj,
wobei uj
divergiert. In (2)
eingesetzt, ergibt sich eine Rekursionsformel für uj,
deren rechte Seite für große uj-1
entwickelt werden kann. Werden
nur die ersten beiden Ordnungen beibehalten, so ergibt sich uj = uj-1 + 1/4 + O(1/uj-1).
Für große
j beschreibt dies ein lineares Wachstum: uj » j/4,
woraus wir auf wj » 4/j
schließen. Das ist das gesuchte asymptotische Verhalten.
Für Alice
ist es also ziemlich unwahrscheinlich, an der Spitze einer langen maternaten
Erblinie zu stehen. Hat Alice vor 1000
Generationen gelebt, so wird es mit der Wahrscheinlichkeit 0.004
eine solche Linie geben, die bis heute reicht -
selbst wenn Alices' Nachkommenschaft genauso reich ist wie jene ihrer
Konkurrentinnen.
Eine interessante
Frage ergibt sich, wenn wir den obigen Graphen noch einmal betrachten:
Im verwendeten Modell ist die Bevölkerungszahl konstant, aber
die Anzahl der Ecken nimmt nach unten hin exponentiell zu. Wie kann
diese Diskrepanz ergeklärt werden? Die Antwort ist, dass verschiedene
Ecken ein- und dasselbe Individuum darstellen können. Genau genommen
wird dann die Verteilung der Töchter und Söhne im obigen
Graphen nicht für jedes Individuum separat gewürfelt. Dennoch
ist die Argumentation, die zu (2)
geführt hat, korrekt, da in den maternalen Erblinien, die von
Alice ausgehen, jedes Individuum höchstens einmal vorkommt, und
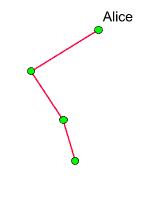
die anderen Erblinien interessieren uns nicht. Wenn die grauen und
alle von ihnen absteigenden Kanten einfach aus dem Graphen entfernt
werden, bleibt nicht viel übrig (linkes Diagramm):
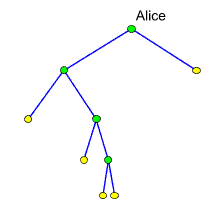
Auch das
rechte Diagramm, in dem die blauen Kanten den vollständigen mitochondriale
Erbgang dargestellen (sie reichen auch bis zu den Söhnen, enden
aber dort), sieht nicht viel reichhaltiger aus. In der letzten (vierten)
Generation darf gerade mal eine Gruppe von zwei Männern Alice
als ihre Clanmutter betrachten. Die maternalen Erblinien sind also
dünn gesät. Fragen wir ganz allgemein: Wie viele Individuen
der j-ten
Generation, die mit Alice durch eine maternale Erblinie verbunden
sich, dürfen wir erwarten? Nennen wir diesen Erwartungswert mj,
so zeigt eine ähnliche Argumentation wie jene, die auf (2)
geführt hat, dass mj = mj-1
für j ³ 2
mit Anfangswert m1 = 2.
Daraus folgt unmittelbar, dass mj = 2
für alle j ³ 1
ist. Es gibt im Mittel (d.h. wenn dieser Prozess oft durchgespielt
wird) in jeder Generation nur zwei Individuen, die maternal mit Alice
verbunden sind, und daher nur eine Frau, für die das gilt. Daraus
können wir abschätzen, wie groß ein typischer heutiger
maternaler Alice-Clan ist: Bezeichnen wir die typische Clangröße
mit
n, so wird es im Mittel nwj
maternale Alice-Nachfahren geben. Das ist aber, wie zuvor argumentiert,
gerade
2, und daher gilt nwj = 2.
Ist j
groß, so ist wj » 4/j,
und wir schließen n » j/2.
Die typische Größe des maternal auf Alice zurückgehenden
Clans ist - unter der Voraussetzung, dass es überhaupt einen gibt
- (in diesem einfachen Modell) halb so groß wie die Anzahl der Generation, die uns von ihr
trennen.
Urmutter oder Clanmutter
zu sein ist also tatsächlich so etwas wie ein Lotteriegewinn. Wer
insgesamt mehr Nachkommen hat, erhöht natürlich die Chance
auf diesen Gewinn, aber der Hauptmechanismus für die Seltenheit
der Evas und Ursulas ist die Seltenheit, mit der sich die roten
Kanten in einem Galton-Watson-Baum zu ununterbrochenen Linien zusammenschließen.
Wir können getrost auch die meisten von Evas und Ursulas Zeitgenossinnen
zu unseren Vorfahren zählen. (Eine numerisch genauere Begründung
dafür werden wir ganz unten nachliefern).
So klein die Wahrscheinlichkeit
für Alice auch sein mag, durch eine maternale Erblinie mit der
Gegenwart verbunden zu sein - zumindest eine
solche Linie muss es in jeder Generation geben, denn maternale
Erblinien können aufsteigend beliebig lange verfolgt werden. Je
weiter wir in die Vergangenheit schreiten, umso weniger dieser Linien
gibt es, bis sie sich schließlich in Eva alle vereinen. In den
Generationen vor Eva gibt es eine einzige maternale Erblinie,
die aufsteigend zum Homo erectus führt und sich schließlich
im Tierreich verliert. Damit wird ein anderer Aspekt beleuchtet, der
in populären Aufsätzen ein bisschen untergeht: Eva stand nicht
unbedingt ganz am Anfang - unsere Vorfahren
können schon einige Zeit als Art existiert haben, bevor sie geboren
wurde. Allerdings waren sie damals noch nicht über die ganze Erde
verstreut. Da in Eva alle von heutigen Menschen ausgehenden maternalen
Linien zusammenlaufen, war sie ziemlich sicher Afrikanerin.
| Ein
verbessertes Modell für Alice (und Ursula) |
Das
bisher betrachtete Modell ist ein bisschen zu einfach, um realistische
Größenordnungen zu reproduzieren, da wir eine stagnierende
Bevälkerungszahl angenommen haben. Eine etwas genaueres Modell
ergibt sich, wenn jeder Mensch (der ins fortpflanzungsfähige Alter
gelangt) im Durchschnitt 2r
Kinder bekommt, die wiederum (je 2r)
Kinder bekommen, usw. Wir nehmen weiters an, dass r > 1
ist, so dass die Bevölkerungszahl exponentiell anwächst. (Dieses
Modell fällt ebenfalls in die Klasse der Galton-Watson-Prozesse,
d.h. des zufälligen Aufbaus eines Baumes). Das oben
betrachtete Modell entspricht dem Fall r = 1.
Der Baum, der Alices Nachkommen nun beschreibt, wird klarerweise mehr
binär sein, sondern Ecken höheren Grades als 3
enthalten. Ist r
nicht ganzzahlig, so wird der Baum nur im Durchschnitt regelmäßig
sein.
Mit einer ähnlichen
Argumentation wie oben kann argumentiert werden,
dass
| wj = 1 - ( 1 - |
wj-1
|
) |
2r |
| 2 |
|
|
(3) |
mit Anfangswert
w0 = 1
ist. Nun bestehen bessere Chancen auf ununterbrochene maternale Erblinien,
da es mehr Nachkommen gibt. Die Folge wj
konvergiert gegen einen Wert w¥ ¹ 0,
der nur von r
abhängt. Er ist die Lösung der Gleichung, die entsteht, wenn
wj
und wj-1
in (3)
durch w¥
ersetzt werden. Ist r
nur ein wenig größer als 1,
so ergibt eine Näherungsberechnung, deren Details wir uns hier
schenken, dass w¥ » 4(r - 1)
ist. Für r - 1 < 0.01
stimmt sie recht genau, und für j > 1/(4(r - 1))
liegt wj
schon sehr nahe bei diesem Grenzwert. (Übungsaufgabe: Leiten Sie
diese Resultate her!)
Wie im obigen
einfacheren Modell können wir den Erwartungswert mj
der Anzahl an Individuen der j-ten
Generation, die mit Alice durch eine maternale Erblinie verbunden sind,
berechnen. Es ergibt sich das inerative System mj = r mj-1
mit Anfangswert m1 = 2r
und Lösung mj = 2r j.
Diese Größe wächst also ebenso schnell (exponentiell)
wie die gesamte Population. Das erklärt, warum Alices Chancen auf
maternale Erblinien steigen. Genau wie oben kann die typische Größe
n
eines heutigen Clans maternaler Alice-Nachfahren berechnet werden.
Es ergibt sich n = 2r j/wj
oder, sofern j > 1/(4(r - 1))
ist,
näherungsweise
Also auch die
typische Clangröße wächst exponentiell.
Nun können
wir unser Modell mit der Wirklichkeit konfrontieren und eine grobe Überschlagsrechnung
machen. Von
den in (4)
enthaltenen Größen ist r
am schlechtesten bekannt. Sehen wir uns an, ob sich aus (4)
eine realistische Größenordnung ergibt. Betrachten wir Ursula,
die vor ungefähr 45 000 Jahren, also
j » 2250
Generationen gelebt hat. Zu ihrem Clan gehören elf Prozent der
europäischen Bevölkerung. Lassen wir die Bevölkerungsentwicklung
der neueren Geschichte außer Acht und gehen um tausend Jahre zurück,
so entspricht das n » 2
Millionen. Um r
aus (4)
zu bestimmen,
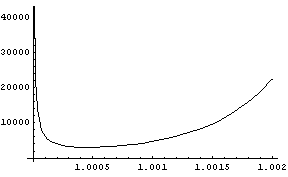
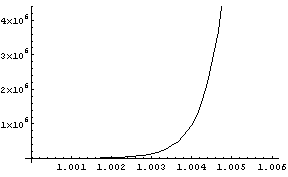
fassen wir die rechte Seite von (4)
als Funktion von r
auf und plotten sie. Hier zwei Plots mit verschiedenen Bereichen von
r :
Da in beiden Bereichen j > 1/(4(r - 1))
gilt, ist die Anwendung von Formel (4)
als gute Näherung für die Clangröße gerechtfertigt.
Im linken Plot kommen die Funktionswerte nicht an die gewünschten
2 Millionen
heran, aber dafür wird eine andere interessante Eigenschaft sichtbar:
es gibt ein Minimum für die Clangröße (das hier bei etwa
3000 Individuen
liegt). Kleinere Clans sind zwar rein theoretisch denkbar, haben aber
offensichtlich "das Maß null". (Zum Vergleich: im obigen
statischen Bevölkerungsmodell r = 1
wäre die Clangröße j/2,
d.h. etwas über 1000,
also viel zu klein). Dem rechten Plot entnehmen wir, dass r » 1.0043
die gewünsche Clangröße von 2
Millionen reproduziert. Dieser Wert passt ganz gut mit dem aus anderen
Quellen abgeschätzten Bevölkerungswachstum während des
eiszeitlichen Europa zusammen. Wir dürfen aber die in ihm steckenden
Unsicherheiten nicht vergessen:
- Formel (4)
stellt eine "typische" Clangröße dar, also einen
Mittelwert aus vielen "Durchgängen" des gesamten Prozesses.
Die zugrunde liegende Verteilung besitzt eine erhebliche Schwankung,
die von der großen Rolle des Zufalls im Galton-Watson-Prozess
herrührt. Tatsächlich führt dieser Zufall dazu, dass
die Wachstumsrate eines Clans von jener der Gesamtbevölkerung
abweichen kann, die Größe r
in (4)
also nicht ganz einheitlich ist (davon abgesehen, dass sie zwischen
lokalen Populationen variieren kann).
- Werden die
anderen europäischen Clans analysiert, so zeigen sich diese Schwankungen.
Besonders hervorstechend ist der Clan der maternalen Nachfahren von
Helena, die vor 20 000 Jahren lebte. Er
umfasst etwa 47%
der europäischen Bevölkerung und muss für sich genommen
die sehr hohe Wachstumsrate von
r » 1.005
gehabt haben.
Die einzigen
Daten, die wir verwendet haben, um zur Abschätzung r » 1.0043
zu gelangen, sind Ursulas Alter und die Größe ihres heutigen
Clans. Beides ist mit Hilfe rein genetischer Methoden ermittelt worden.
Was wir also soeben gefunden haben, ist eine von anthropologischen und
archäologischen Methoden unabhängige Berechnung der
Größenordnung des frühen Bevölkerungswachstums
- wieder ein erstaunliches Resultat!
| Eva
und ihre Zeitgenossen |
Wir
benutzen nun das soeben aufgestellte verbesserte Modell, um auch etwas
über Eva zu sagen. Insbesondere werden wir eine Begründung
dafür finden, warum die Menschheit zu Evas Zeiten kleiner war als
man vielleicht annehmen möchte.
In
Eva laufen alle maternalen Erblinien der heutigen Menschen zusammen.
Wie oben berechnet, ist
für jede beliebige Frau die Wahrscheinlichkeit, eine j
Generationen ununterbrochene maternale Linie zu besitzen, (für
große j)
durch w¥ » 4(r - 1)
gegeben. Im Mittel sind also in einer frühen Generation (g/2) × w¥
solcher Frauen zu erwarten, wobei g
die Gesamtgröße der damaligen Population bezeichnet. Schreiten
wir in die Vergangenheit zurück, so wird diese (theoretische) Zahl
immer kleiner, bis sie schließlich die Größenordnung
1
erreicht. Eva kann nicht nach dieser Zeit gelebt haben (sonst
könnte sie nicht die einzige derartige Frau ihrer Generation sein).
Wahrscheinlich hat sie ungefähr zu dieser Zeit gelebt. Die Eva-Bedingung
lautet
also
Setzen wir die
für sehr frühe Zeiten geschätzte Wachstumsrate r = 1.001
ein, so ergibt sich g » 500.
Für den Fall, dass die Wachstumsrate damals noch kleiner war, setzen
wir r = 1.0002
ein und erhalten g » 2500.
Um diese numerische
Berechnung ein bisschen sorgfältiger zu gestalten, bemerken wir,
dass (5)
keinen Bezug zu "heute" enthält! Dieser Umstand kann
dazu benutzt werden, g
und r
über die Bevölkerungszahl zu einem früheren Zeitpunkt,
als die Wachstumsrate noch einigermaßen konstant war, miteinander
zu verbinden:
j
Generationen nach Eva ist die Bevölkerungszahl nj = g r j.
Ist nj
bekannt, kann r
aus (4)
eliminiert werden. Wir betrachten dazu die ersten hunderttausend Jahre
nach Eva (j = 5000)
und setzen die Bevölkerungszahl n5000
(vor 50 000 Jahren) mit 3 Millionen an. Daraus ergibt sich
r = (3×106/g)1/5000,
womit die Eva-Bedingung
zu
| 2 g |
[ |
( |
3 ×106
|
) |
1/5000 |
- 1] |
» 1 |
|
| g |
|
|
(6) |
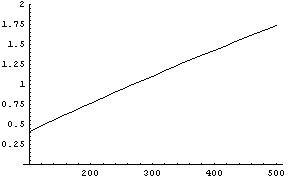
wird. Die (numerisch
sehr unsichere) Wachstumsrate scheint in dieser Gleichung nicht mehr
auf. Plotten wir den Ausdruck auf der linken Seite als Funktion der
einzigen verbliebenen Variable g,
so ergibt sich
was bei knappen dreihundert Individuen den Wert 1
annimmt. Daraus wiederum folgt r » 1.0019
(ein Wert, der für die ersten hunderttausend Jahre nicht unplausibel
klingt). Trotz der unsicheren Details sind die Größenordnungen
relativ robust: die Menschheit war zu Evas Zeiten sehr klein.
Das ist ein
bemerkenswertes Resultat. Um die Größe der Menschheit zur
Zeit Evas abzuschätzen, war nur ein einziger numerischer Wert
nötig: die Wachstumsrate r,
wenn Gleichung (5)
benutzt wird, oder, wenn mit (6)
argumentiert wird, die Zahl der Menschen 5000
Generationen nach Eva (was letztlich ebenfalls auf eine Abschätzung
von r
hinausläuft). Keine genetischen Daten, sondern lediglich ein bisschen
Wahrscheinlichkeitsrechnung und eine Grundvorstellung über das
frühe Bevölkerungswachstum waren notwendig, um ein starkes
Indiz dafür zu finden, dass die Menschheit zu Lebzeiten Evas nicht
viel mehr als einige tausend, möglicherweise aber noch weniger
Individuen zählte!
| Poiniere
und die Zeit nach Eva |
Machen wir einen
Blick in die Zukunft: Wenn die Menschheit noch einige hundertausende
Jahre besteht, wird Eva weiterhin die ihr zukommende Rolle spielen.
Das kommt in der Beziehung (5)
dadurch zum Ausdruck, dass sie sich nicht auf einen bestimmten Zeitpunkt
bezieht. Die Wahrscheinlichkeit, dass eine später geborene Frau
durch die Zufallsgesetzmäßigkeiten des Galton-Watson-Prozesses
diese Rolle übernehmen wird, ist extrem klein, zumindest solange
die Wachstumsrate r
so groß ist wie heute. Ist also Eva für alle Zeiten
die Urmutter? Dabei müssen wir ein bisschen aufpassen: Der
Begriff der Urmutter bezieht sich immer auf eine Gesamtheit von Individuen,
in unserem Fall auf die heute lebenden Menschen. Die Frage nach der
jüngsten gemeinsamen maternalen Vorfahrin aller Primaten (Menschenaffen
und Menschen) bewegt längst nicht so viele Gemüter! In diesem
Sinn kann sich die Urmutterschaft aber relativ schnell ändern.
Damit stehen wir vor der Frage nach der Entstehung neuer Populationen
und Arten.
Stellen wir uns
vor, eine kleine Gruppe von, sagen wir, g = 50
Menschen (25
Männer und 25
Frauen) besiedelt einen fernen Planeten, verliert den Kontakt zur Erde
und entwickelt eine eigene Identität. Wenn der genetische Austausch
mit dem Rest der Menschheit abreißt, können ihre Nachkommen
einige hunderttausend Jahre später sogar zu einer eigenen Art geworden
sein. Wer wird dann deren Urmutter sein? Hier bestehen zwei Möglichkeiten:
- Zunächst ist die jüngste
gemeinsame maternale Vorfahrin aller 25
Pionierinnen nicht unbedingt Eva. Wenn beispielsweise alle Pionierinnen
dem Helena-Clan angehören, so wird Helena oder eine ihrer maternalen
Nachfahrinnen diese Rolle einnehmen.
- Ist die Wachstumsrate der
neuen Population sehr groß, d.h. ist 2g(r - 1) >> 1
(wie es für die heutige Menschheit der Fall ist),
so wird wenig Chance
bestehen, dass maternale Erblinien aus Mangel an Töchtern unterbrochen
werden.
- Ist r
hingegen eher klein, sagen wir
r < 1 + 1/(2g) =
1 + 1/100 = 1.01,
so wird eines Tages die Eva-Bedingung (5)
erfüllt sein, und eine der Frauen dieser fernen Zeiten bekommt
die Chance, die einzige maternale Ahnin einer neuen Art zu werden.
- Spaltet sich die Population
alsbald in mehrere Gruppen auf, um sich über ihren Planeten zu
verteilen, so wird keine Frau in einer der Gruppen Vorfahrin
aller Pionier-Abkömmlinge sein können. Ihre jüngste
gemeinsame maternale Ahnin ist damit in gewisser Weise "fixiert"
- und genau das gilt ja auch für Eva,
die vor der Auswanderung von (vermutlich kleinen) Gruppen aus
Afrika gelebt haben muss. Ist die Isolation der Gruppen allerdings
vollkommen und dauert sehr lange, so wird sich die aufgespaltete Population
in mehrere Arten ausdifferenzieren, und jede mag sich fortan nur für
ihre Urmutter interessieren, und so wiederholt sich die Geschichte...
Aus diesen Überlegungen
können wir Einiges über den Charakter der Urmutterschaft und
der Eva-Bedingung lernen. Zwei Mechanismen wirken in die gleiche Richtung:
- Je kleiner die Pionierguppe,
umso größer ist die Aussicht auf eine baldige Eva-Nachfolge.
Pionier-Populationen bilden oft einen "Flaschenhals"
von nur wenigen Individuen. (Ein ähnlicher Effekt tritt ein,
wenn eine Population dezimiert wird und dem Aussterben knapp entgeht.
Wie wir gesehen haben, scheint es den Geparden
so gegangen zu sein).
- Eine kleine Wachstumrate
begünstigt das Abreißen maternaler Erblinien. Erinnern
wir uns an das einfache Modell einer konstanten Bevölkerungszahl
(r = 1),
das wir oben betrachtet
haben: In diesem Extremfall strebt für jede Frau die Wahrscheinlichkeit,
eine lange maternale Erblinie in die Zukunft zu besitzen, mit wachsender
Länge der Linie gegen null. In einem solchen Modell erwarten
wir das Auftreten einer Reihe von Frauen, die zu unregelmäßigen
(durch den Galton-Watson-Zufall bestimmten) Zeitpunkten die jeweils
bisherige Urmutter beerben.
Die Zeit, vor der
die jüngste maternale Vorfahrin einer Gruppe von Individuen gelebt
hat, ist in gewisser Hinsicht vergleichbar mit dem "Ereignishorizont"
in der Kosmologie. Sie gibt an, wie weit die maternale Abstammung
zurückverfolgt werden kann, bevor sich alles in einer einzigen
Linie verliert - nicht mehr und nicht weniger.
Der Begriffe der "Urmutter" und der "Clanmutter"
leisten gute Dienste, wenn es darum geht, unsere Vorgeschichte aufzuklären,
und wenn den Missverständnissen, die sie nahelegen, widerstanden
wird.
Motiviert durch
die Tatsache, dass Mitochondien-DNS immer von der Mutter vererbt wird,
haben wir uns nun ausführlich mit maternalen Erblinien beschäftigt.
Wir hätten theoretisch auch paternale Erblinien analysieren
können und wären zu den selben Ergebnissen gelangt. Die aufsteigenden
väterlichen Linien neigen ebenso wie die mütterlichen dazu,
sich zusehends zu vereinigen und in ferner Vergangenheit auf wenige
Personen zu reduzieren - den Clanvätern,
an deren Spitze Adam steht. Paternale Clans sind ebensolche Zufallsprodukte
eines Galton-Watson-Prozesses wie maternale, so dass wir die obige Analyse
genau übernehmen können. Klar ist auch, dass Adams Zeitgenossen,
von denen heute niemand paternal abstammt, dennoch zu unseren Vorfahren
zählen, dass die maternalen sich nicht mit den paternalen
Clans decken und dass Adam nicht Evas Gefährte war.
Was fehlt, ist
eine genetische Einheit, die nur in der männlichen Linie vererbt
wird. Diese gibt es tatsächlich: das Y-Chromosom, das vom Vater
auf den Sohn übertragen wird (während Frauen es überhaupt
nicht besitzen, sondern statt dessen ein zweites X-Chromosomen haben).
Y-Chromosomen sind komplexer aufgebaut und schwieriger zu sequenzieren
als die mitochondrialen DNS-Ringe, und daher hat es länger gedauert,
Bereiche in ihnen auszumachen, die die Rolle der Mitochondrien-Kontrollregion
übernehmen können. Seit einigen Jahren ist es aber dennoch
gelungen, und mittlerweile liegt eine wachsende Menge von Daten über
die paternale Abstammungsgeschichte vor. Es ist keine Überraschung,
dass deren Charakteristika jenen der maternalen Geschichte ähneln.
Für Europa wurden bisher 10 paternale Clans identifiziert.
So rundet sich
das Bild der "anderen Genetik", in der es keine Rekombination
gibt, ab. Maternale und paternale Erblinien, identifiziert über
die in Mitochondrien und Y-Chromosomen weitergegebene DNS und die in
ihr angesammelten Mutationen, gehören zu den eindrucksvollsten
Hilfsmitteln auf der Suche nach unserem Ursprung.
| Wieviele
Nachkommen hat der Mensch? |
Um nicht die Vorstellung
aufkommen zu lassen, die letzten gemeinsamen Vorfahren aller heute lebenden
Menschen hätten vor hunderttausend Jahren gelebt, machen wir zum
Abschluss eine interessante Abschätzung. Wir betrachten einen bestimmten
Menschen
x (zum Beispiel Julius Cäsar), zu dessen Zeit
n0 = g Menschen lebten.
Bei einer Wachstumsrate r
umfasst die j-te
Generation nach ihm nj
Individuen, wobei nj = r nj-1
ist. Nun fragen wir, wieviele Nachkommen von x
- unter der vereinfachten Annahme der Zufallspaarung
- in der j-ten
Generation leben. (Dabei beschränken wir uns nicht auf
maternale oder paternale Abstammungslinien). Gibt es in der j-ten
Generation kj
und in der (j-1)-ten
Generation kj-1
Nachkommen von x,
so schätzen wir kj
aus kj-1
folgendermaßen ab: Da die relative Häufigkeit der Nachkommen
von x
in der (j-1)-ten
Generation pj-1 = kj-1/nj-1
ist, wird eine Zufallsverbindung
mit einer Wahrscheinlichkeit von 1 - (1 - pj-1)2
zwischen Individuen eingegangen, von denen zumindest ein Partner Nachkomme
von x
ist. Da es in dieser Generation nj-1/2
Paare gibt und jedes Paar durchschnittlich 2r
Kinder hat, erwarten wir in der j-ten
Generation ungefähr kj = r nj-1(1 - (1 - pj-1)2)
Nachkommen von x.
Mit pj = kj/nj
entsteht daraus die Rekursionsformel pj = 1 - (1 - pj-1)2,
die zusammen mit der Anfangsbedingung p0 = 1/g
die gestellte Frage beantwortet. Ihre explitzite Lösung
lautet
| pj = 1 - (1 - 1/g)2 j . |
(7) |
Die relative Häufigkeit
der Nachkommen von x
in der j-ten
Generation nach x
hängt nicht von der Wachstumsrate r
ab, was die numerische Auswertung erleichtert. Welchen Anteil haben
die Nachkommen von x
40 Generationen
(als etwa 800
Jahre) später? Setzen wir j = 40,
so hängt diese Größe nur mehr von g
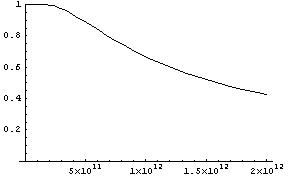
ab. Hier ein Plot von p40
als Funktion von g:
Die Funktionswerte
sind für Populationszahlen kleiner als astronomische 1011
extrem nahe bei 1.
Daher ist in diesem Modell nach 40
Generationen praktisch jeder Mensch ein Nachkomme von x!
Die Bedingung der Zufallspaarung
ist in großen menschlichen Populationen (wie den Bewohnern eines
Kontinents) nur für längere Zeiträume näherungsweise
erfüllt. Dafür sorgen schon die gelegentlichen Auswanderer,
die sich fern der Heimat niederlassen.
Was allerdings
berücksichtigt werden muss, ist, dass nicht jeder Mensch Nachkommen
in die Welt setzt. Hat x
aber Kinder, und haben diese Kinder wiederum Kinder, so ist die Wahrscheinlichkeit,
dass die gesamte Nachkommenschaft von x
ausstirbt, bereits sehr klein.
Dadurch dauert es etwas länger
als durch (7)
beschrieben, bis die gleiche
Wirkung eintritt, aber das Wesentliche dieses Resultats bleibt davon
unberührt: Fast jeder heute lebende Mensch kann mit großer
Wahrscheinlichkeit Julius Cäsar (der mehrere Kinder hatte)
zu seinen Vorfahren zählen! Das gilt sogar für die
Nachkommen der amerikanischen Urbevölkerung, und zwar dank der
Vermischung mit Europäern ab dem 16. Jahrhundert. Nach demselben
Mechanismus ist Konfuzius (von dem berichtet wird, dass er Kinder hatte)
ziemlich sicher ein Vorfahr fast aller Asiaten, und jeder dieser
Nachfahren, der um das Jahr 1200 n. Chr. nach Afrika gekommen,
dort geheiratet und Kinder gezeugt hat, die wieder Kinder hatten, ist
heute mit großer Wahrscheinlichkeit Vorfahr praktisch aller heutigen
Afrikaner - woraus folgt, dass fast die gesamte
Bevölkerung Afrikas höchstwahrscheinlich von Konfuzius abstammt!
Dieser erstaunliche
Befund löst übrigens auch das Rätsel vom "Ahnenschwund":
Wenn ich 2 Eltern, 4 Großeltern, 8 Urgroßeltern, 16 Ururgroßeltern
(allgemein 2 j
Ur j-2großeltern)
habe, so übersteigen die Glieder diese Folge bald (ab j » 30)
die Zahl der lebenden Menschen. Tatsächlich sind viele der in
dieser Rechnung als verschieden veranschlagten Vorfahren miteinander
identisch. Das Resultat (7)
kann so interpretiert
werden, dass die Zahl der Vorfahren eines heutigen Menschen vor 40
Generationen einen Großteil der damaligen Bevölkerung ausmachte!
Allerdings
sollte dazugesagt werden, dass die Wahrscheinlichkeit, von einem dieser
Ahnen ein bestimmtes ("seltenes") Allel zu erben, sehr klein
ist und davon abhängt, wieviele Vererbungswege das Allel innerhalb
des Verwandtschaftsgraphen nehmen kann (d.h. welcher Verwandtschaftsgrad
zu diesem Ahnen besteht). Daher werden die "Cäsar-Gene"
in der europäischen Urbevölkerung häufiger vertreten
sein als in der amerikanischen.
Der genetische
Austausch zwischen menschlichen Populationen ist -
und war - also lebhafter, als man es intuitiv
vielleicht annehmen würde. Das erklärt, wieso der menschliche
Genpool zu gut durchmischt ist, um die Definition klar abgegrenzter
Kategorien ("Rassen") zuzulassen. Auch die "Clans"
sind theoretische Konstruktionen, die zwar der Erforschung unserer Geschichte
dienen, wohl kaum aber mit "Merkmalen" (außer ein paar
Basenabfolgen) in Zusammenhang stehen. Die meisten der ZeitgenossInnen
Evas, Adams und Ursulas zählen - soweit
sie Kinder hatten - ziemlich sicher zu den
Vorfahren aller heute lebenden Menschen. Vom Standpunkt des gesamten
Genpools aus betrachtet sind die ununterbrochenen maternalen und paternalen
Erblinien, denen diese Individuen ihre Positionen verdanken, bedeutungslos.
Webseiten:
Bücher:
- Bryan Sykes, Die sieben Töchter
Evas, Bastei Lübbe, 2001
- Bryan Sykes, Keine Zukunft für
Adam, Bastei Lübbe, 2003
- Luigi Cavalli-Sforza,
Gene, Völker, Sprachen, dtv, 1996
- Steve Olson, Herkunft und
Geschichte des Menschen, Berlin Verlag, Berlin, 2003.
- Spencer Wells, Die Wege
der Menschheit, S. Fischer, 2003
|