|
Von Graphen, Genen und dem WWW

Online-Skriptum
Der Bayessche Satz der Wahrscheinlichkeitsrechnung
| Wahrscheinlichkeitsbäume
und Zufallsprozesse |
Wahrscheinlichkeitsbäume
sind bequeme Hilfsmittel zur Darstellung von Zufallsprozessen.
Ecken repräsentieren Zufallsverzweigungen, Kanten stehen für
die entsprechenden Ereignisse. Wahrscheinlichkeitsbäume sind kantengewichtete
Graphen: jeder Kante wird eine Zahl (die Wahrscheinlichkeit für
das Eintreten des Ereignisses, das sie darstellt) zugeordnet. Der häufigste
Anwendungstyp besteht darin, die Wahrscheinlichkeit eines Ereignisses
zu berechnen, indem die Gewichte der Kanten, die von der Wurzel zu ihm
führen, miteinander multipliziert werden.
In der Praxis tritt
jedoch oft eine andere Fragestellung auf: Ein Zufallsereignis (z.B.
ein Messwert) ist eingetreten, und man möchte nun gerne seine Ursache
kennen. Falls das Ereignis mehrere Zufallsprozesse als "Ursache"
haben kann, lässt sich zwar seine Eintrittswahrscheinlichkeit in
jedem diese Prozesse berechnen, aber das beantwortet nicht die Frage,
mit welcher Wahrscheinlichkeit jeder dieser Prozesse der Verursacher
gewesen ist.
Die Fragestellung
führt zur Betrachtung bedingter Wahrscheinlichkeiten mit "vertauschten
Argumenten". Vereinfacht ausgedrückt, stellt sich die Situation
so dar: Die Berechnung von P(Ereignis|Prozess)
ist sehr einfach, aber eigentlich ist P(Prozess|Ereignis)
gesucht. Für eine solche Vertauschung der Argumente ist der Satz
von Bayes zuständig. Daher
kann die Lösung des Problems ganz im Rahmen der elementaren Wahrscheilichkeitsrechnung
erfolgen, aber es ist nicht leicht, unter dem Bayesschen Satz mehr zu
verstehen als eine abstrakte Identität (eine anzuwendende "Formel").
Zwei Hilfsmittel können die Behandlung derartiger Probleme erleichtern
und verleihen dem Satz von Bayes eine anschauliche Note: der geschickte
Einsatz von (miteinander kombinierten) Wahrscheinlichkeitsbäumen
und der Begriff der Apriori-Wahrscheinlichkeit.
Letzterer hat darüber
hinaus auch eine praktische Dimension: Apriori-Wahrscheinlichkeiten
können oft sehr genau bestimmt werden, manchmal aber stecken in
ihnen äußerst unsichere Annahmen.
Wir beginnen mit
folgender Situation: Jemand besitzt zwei "Zufallsgeneratoren",
die zwei Ereignisse 0
und 1
als mögliche Ausgabewerte besitzen:
- Eine Münze, die
0
oder 1
als mögliche Wurfresultate ergibt, und zwar mit jeweils gleicher
Wahrscheinlichkeit
1/2.
- Einen Würfel,
der in besonderer Weise präpariert ist: Auf 2
Seiten steht 0,
auf 4
Seiten steht 1.
Daher wird 0
mit Wahrscheinlichkeit 1/3
und 1
mit Wahrscheinlichkeit 2/3
gewürfelt werden.
Mathematisch betrachtet,
stellt jedes der beiden Geräte eine Wahrscheinlichkeitsverteilung
(einen Zufallsprozess) für die Ereignismenge
{0, 1}
dar. Die zugehörigen Baumdiagramme sehen so aus:
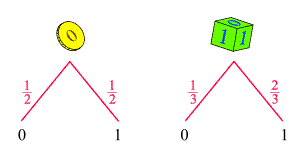
Nun stellen wir
uns vor, mit einem der beiden Geräte wurde eine Zufallszahl
ermittelt, und das Resultat war 1.
Ist es möglich, Mutmaßungen darüber anzustellen, welche
der beiden Methoden benutzt wurde? Solle man in einer Wette eher auf
Münze oder eher auf Würfel setzen? Wir heben die beiden 1er
in den Wahrscheinlichkeitsbäumen hervor:
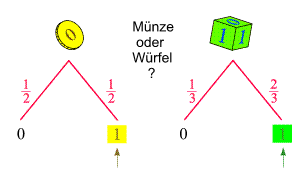
Können wir
eine Wahrscheinlichkeitsaussage darüber machen, ob es sich eher
um den Münz-1er
oder eher um den Würfel-1er
handelt? Das ist klarerweise nur dann möglich, wenn eine Annahme
darüber gemacht wird, mit welchen Apriori-Wahrscheinlichkeiten
Münze und Würfel zum Zug kommen.
Wir stellen uns
nun vor, verdeckte Recherchen ergeben, dass der Urheber dieses Spiels
in der Regel die Münze bevorzugt: Es wählt sie mit Wahrscheinlichkeit
4/5, während
er zum Würfel nur mit Wahrscheinlichkeit 1/5
greift. Das sind genau die benötigten Apriori-Wahrscheinlichkeiten!
Wir können nun den Auswahlprozess zwischen den Geräten vor
unsere - bisher getrennt betrachteten -
Wahrscheinlichkeitsbäume "schalten" und diese damit in
einen einzigen Baum einbauen:
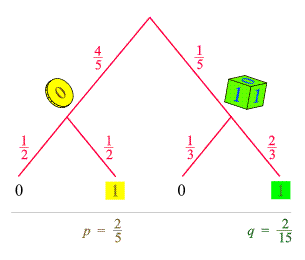
Jetzt ist eine
Rechnung möglich. Vier Dinge können passieren, mit folgenden
Wahrscheinlichkeiten:
- 0,
stammt von der Münze: 2/5
- 1,
stammt von der Münze: 2/5
(im Diagramm als
p bezeichnet)
- 0,
stammt vom Würfel: 1/15
- 1,
stammt vom Würfel: 2/15
(im Diagramm als q bezeichnet)
Die Wahrscheinlichkeiten,
mit der die beiden 1er
auftreten (die Zahlen p und q), sind der Schlüssel zur Antwort auf unsere Frage.
Sie erlauben unmittelbar die Anwendung der Elementarformel
| Wahrscheinlichkeit = |
Zahl
der günstigen Fälle
|
. |
| Zahl
der möglichen Fälle |
|
(1) |
Was sind die "günstigen",
was die "möglichen" Fälle? Um das ganz explizit
zu sehen, nehmen wir an, dass das Spiel 1500
mal durchgeführt wird und schreiben anstelle der Wahrscheinlichkeiten
(d.h. der erwarteten relativen Häufigkeiten) die erwarteten
absoluten Häufigkeiten zu den einzelnen Kanten (dazu fügen
an der Spitze des obigen Diagramms die Gesamtzahl 1500
ein und multiplizieren alle Wahrscheinlichkeiten mit dieser):
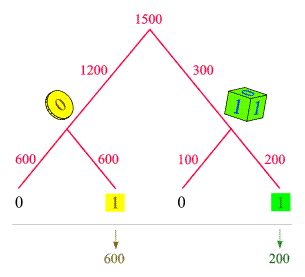
Dabei ignorieren
wir die erwarteten statistischen Schwankungen. (Statt 1500
kann N
gesetzt und beliebig groß gemacht werden). Wir interessieren uns
nur für die Fälle, in denen das Resultat 1
ist. Das geschieht insgesamt 800
mal. In 600
Fällen wurde die Münze, in 200
Fällen wurde der Würfel benutzt. Die Zahl der "möglichen"
Fälle ist daher 800,
die Zahl der "günstigen" Fälle ist 600
für den 1er
vom "Münzzweig" und 200
für den 1er
vom "Würfelzweig". Die entsprechenden Wahrscheinlichkeiten
sind 600/800 = 3/4
und 200/800 = 1/4,
womit das Problem gelöst ist. (Wir würden daher in einer Wette
auf Münze setzen und sie mit der Wahrscheinlichkeit 3/4
gewinnen).
Auf die Gesamtzahl
der durchgeführten Spiele (1500)
kommt es natürlich nicht an - sie kürzt
sich aus der Rechnung heraus. Wir können statt dessen die Wahrscheinlichkeiten
des darüberstehenden
Diagramms benutzen:
| Wahrscheinlichkeit, dass die Münze benutzt wurde = |
p
|
|
|
p + q
|
|
(2) |
| Wahrscheinlichkeit, dass der Würfel benutzt wurde = |
q
|
|
|
p + q
|
|
(3) |
Im ersten Fall
ergibt sich (2/5)/(2/5 + 2/15) = 3/4,
im zweiten Fall finden wir (2/15)/(2/5 + 2/15) = 1/4.
Es sind also nur die beiden Zahlen p und q sind nötig, um das Problem zu lösen. Die Wahrscheinlichkeiten
dafür, dass der zufallsgenerierte 1er
von der Münze oder vom Würfel stammt, verhalten sich wie p : q, d.h. wie 2/5 : 2/15
(oder, gekürzt, wie 3 : 1).
Die Nenner in (2)
und (3)
dienen lediglich der Normierung.
Der Lösungsvorgang
kann in Stichworten so rekapituliert werden:
- Die beiden Prozesse (Münze
oder Würfel), von denen einer der Verursacher des bereits
eingetretenen Ereignisses war, werden durch getrennte Wahrscheinlichkeitsbäume
dargestellt.
- Es müssen Annahmen über
die Apriori-Wahrscheinlichkeiten getroffen werden, mit denen einer
der beiden Prozesse ausgewählt wird.
- Diese erlauben es, die beiden
- bislang getrennt betrachteten -
Wahrscheinlichkeitsbäume zu einem einzigen zusammenzufügen.
- Das betrachtete Ereignis
(1)
tritt in diesem Baum zwei mal als mögliches Resultat des
Gesamtprozesses auf, aufgetrennt nach den Prozessen, die jeweils für
es verantwortlich sein können (Münze oder Würfel).
- Die entsprechenden Wahrscheinlichkeiten
der einzelnen Zweige - sie ergeben sich
durch numerische Auswertung des Baums -
verhalten sich wie die gesuchten Wahrscheinlichkeiten.
Wir wollen nun
kurz überlegen, wie wir diesen Lösungsweg formalisieren können.
Unter Benutzung
des oben konstruierten
Wahrscheinlichkeitsbaumes können wir zurückverfolgen, wie
die Zahlen p und q
zustande kommen:
|
p = Apriori-Wahrscheinlichkeit für Münze ×
P(1|Münze) =
(4/5)(1/2) =
2/5 |
(4) |
|
q = Apriori-Wahrscheinlichkeit für Würfel ×
P(1|Würfel) =
(1/5)(2/3) =
2/15 |
(5) |
Dabei verwenden
wir die übliche Notation P(A|B)
für bedingte Wahrscheinlichkeiten. Wird der senkrechte Strich als
"unter der Voraussetzung" gelesen, sollte die Bedeutung
dieser Schreibweise auch ohne großen Definitionsaufwand klar sein:
- P(1|Münze)
ist die Wahrscheinlichkeit, mit der Münze 1
zu werfen (1/2),
- P(1|Würfel)
ist die Wahrscheinlichkeit, mit dem Würfel 1
zu erzielen (2/3).
Diese beiden Zahlen
ergeben sich aus den für Münze und Würfel charakteristischen
Wahrscheinlichkeitsverteilungen und haben nichts mit dem Auswahlprozess
zwischen ihnen zu tun.
Die Regel, die
wir dabei "entdeckt" haben, ist genau der Satz von Bayes.
Um ihn etwas allgemeiner zu formulieren, betrachten wir ein (endliches)
Ensemble von Zufallsprozessen, aus dem einer ausgewählt
wird und das Eintreten (oder Nicht-Eintreten) gewisser Ereignisse zur
Folge hat. Zwei Arten von Wahrscheinlichkeiten treten auf:
- Auswahl zwischen den Prozessen:
Jeder der Prozesse besitzt eine gewisse Apriori-Wahrscheinlichkeit,
ausgewählt zu werden. Die Apriori-Wahrscheinlichkeit des k-ten
Prozesses nennen wir P(k).
- Charakterisierung der
einzelnen Prozesse: Die Wahrscheinlichkeit, dass der k-te
Prozess (für sich betrachtet) das Eintreten eines Zufallsereignisses
A
zur Folge hat, schreiben wir in der Form P(A|k).
Wieso trennen
wir begrifflich zwischen diesen beiden Typen von Wahrscheinlichkeiten?
Dafür gibt es zwei Gründe:
- Diese Unterscheidung ist in vielen Aufgabenstellungen hilfreich,
da sie die zugrundeliegende Situation strukturiert.
- In der Praxis kommt es oft vor, dass die Apriori-Wahrscheinlichkeiten
schlecht bekannt sind und aufgrund mehr oder weniger gesicherter
Annahmen geschätzt werden müssen, um überhaupt
eine Aussage zu ermöglichen. Mit anderen Worten: Es steht
eine Reihe gut bekannter Zufallsprozesse zur Verfügung, aber
es ist schlecht bekannt, mit welcher Wahrscheinlichkeit einer
von ihnen zum Zug kommt. Diese prinzipielle Logik tritt etwa im
obigen Münz-Würfel-Beispiel zu Tage. Dass der Urheber
dieses Spiels mit Wahrscheinlichkeit 4/5
die Münze wählt, kann stellvertretend für eine
solche Schätzung stehen. Als physikalisches Beispiel werden
wir im nächsten Abschnitt
das Problem der Bestimmung von Quantenzuständen diskutieren.
Bei der Problematik der unsicheren Apriori-Wahrscheinlichkeiten
spielt natürlich auch ein bisschen Philosophie mit: Wenn
wir beispielsweise unser Münz-Würfel-Spiel so abändern,
dass der Urheber immer zum selben (uns nicht bekannten)
Gerät greift, so bleibt (zumindest wenn das Spiel zuvor noch
nie gespielt wurde) nichts übrig, als für Münze
und Würfel die gleiche Apriori-Wahrscheinlichkeit
1/2
anzusetzen. Dieser Wahrscheinlichkeitsbegriff ist aber nun ein
gänzlich anderer als die "Voraussage relativer Häufigkeiten".
Satz von Bayes:
Tritt das Ereignis
A ein, und ist unbekannt, welcher der Prozesse
zuvor ausgewählt wurde, so ist die Wahrscheinlichkeit, dass es
der k-te
Prozess war, durch
P(es war der k-te Prozess) =
|
P(k) P(A|k)
|
|
|
|
|
(6) |
gegeben, wobei
sich die Summe im Nenner über alle Zufallsprozesse erstreckt, die
zur Auswahl stehen. Dieser Satz lässt sich in natürlicher
Weise auf (abzählbar- und überabzählbar-)unendliche Ensembles
von Wahrscheinlichkeitsverteilungen verallgemeinern.
Der
Nenner in (6)
ist für alle k
gleich. Er spielt hier lediglich die Rolle einer Normierung, d.h.
der Sicherstellung, dass sich alle Wahrscheinlichkeiten (6)
zu 1 aufsummieren.
Daher wird (6)
auch manchmal in der einfacheren Form
| P(es war der k-te Prozess) = |
c P(k) P(A|k)
|
|
|
(6') |
geschrieben,
wobei c
eine Konstante ist, deren Wert sich daraus ergibt, dass die Summe
dieser Wahrscheinlichkeiten über alle k
gleich 1
ist.
Oft
wird der Nenner der rechten Seite von (6)
als P(A)
und die linke Seite von (6)
als P(k|A)
geschrieben, womit der Satz die Form
| P(k|A) = |
P(k) P(A|k)
|
|
| P(A) |
|
(6'') |
annimmt. Sie
sieht zwar einfacher aus als (6),
aber damit werden unsere ursprüngliche Intention und die Tatsache,
dass sich der Nenner in einfacher Weise aus den anderen auf der rechten
Seite vorkommenden Größen P(k)
und
P(A|k) ermitteln
lässt, ein bisschen zugedeckt.
Da ein Zufallsprozess
auch als statistisches Ensemble verstanden werden kann, ist unser
"Ensemble von Zufallsprozessen" tatsächlich ein "Ensemble
von Ensembles". (Es wird eine Probe aus einem von mehreren Ensemble
gezogen, und man wüsste gern, aus welchem. Beispiel: Es wird
eine Kugel aus einer von mehreren Urnen, deren Inhalte sich voneinander
unterscheiden, gezogen, und man wüsste gern, aus welcher).
In unserem obigen
Beispiel kann k
die Werte "Münze" und "Würfel" annehmen,
und das Ereignis A
steht für 1.
Der Ausdruck (6)
wird genau zu (2)
und (3),
mit (4)
und (5)
eingesetzt.
Wir fassen zusammen:
Aufgaben, in denen aus der Wirkung eines Zufallsprozesses auf
die Natur des sie verursachenden Prozesses rückgeschlossen
werden soll, können - nach Annahme von
Apriori-Wahrscheinlichkeiten für die in Frage kommenden Prozesse
-
- durch die "Zusammenfügung
getrennter Wahrscheinlichkeitsbäume" (graphische Methode)
oder
- durch die formale Anwendung
des Bayesschen Satzes
gelöst werden.
(Sind nur endlich viele Prozesse im Spiel, so sind beide Methoden äquivalent).
Für Unterrichtszwecke wird die erste oft die gegebene sein (insbesondere,
wenn die Anzahl der zur Auswahl stehenden Prozesse und die Anzahl der
möglichen Ereignisse klein ist). Nach mehrmaliger selbständiger
Anwendung durch die SchülerInnen sollte sich auch ein gewisses
Verständnis für die Formalisierung dieses Vorgangs, d.h. für
die zweite Methode erzielen lassen.
Übungsbeispiel:
Formulieren Sie den Satz von Bayes in der Formulierung ( 6' )
in Worten !
Um den (wahrscheinlichsten)
Verursacher gewisser Erscheinungen ausfindig zu machen, werden in der
Praxis viele Daten erhoben. Mit jeder gemachten Beobachtung (durchgeführten
Messung) wächst die Sicherheit. Betrachten
wir wieder unser obiges Münze-Würfel-Beispiel. Das Ereignis
A
stehe nun für die Realisierung einer Folge von Zufallszahlen.
Wie nehmen an, es wurde die Folge 011011
in 7 voneinander unabhängigen Würfen mit einer der
beiden Methoden (Münze oder Würfel) erhalten. Wie würden
wir diesmal wetten? Gefühlsmäßig sieht es diesmal sehr
nach dem Würfel aus, da doppelt so viele 1er
vorkommen wie 0er.
Das entspricht genau der Wahrscheinlichkeitsverteilung des Würfels.
Wie sicher können wir uns sein? Wir sparen uns nun das Zeichnen
eines Diagramms. Die Wahrscheinlichkeiten für das Eintreten der
Folge 011011
sind
| P(011011|Münze) |
= P(0|Münze)2 P(1|Münze)4 |
= (1/2)2 (1/2)4 |
| P(011011|Würfel) |
= P(0|Würfel)2 P(1|Würfel)4 |
= (1/3)2 (2/3)4 |
|
(7) |
Die numerischen
Werte dieser Zahlen sind (gerundet) 0.016
und 0.022.
Die Zufallsfolge 011011
zu erhalten, ist für den Würfel etwas wahrscheinlicher als
für die Münze. Die Anwendung des Bayesschen Satzes mit den
Apriori-Wahrscheinlichkeiten
P(Münze) = 4/5
und P(Würfel) = 1/5
ergibt
| P(es war die Münze) |
= c P(Münze) P(011011|Münze) |
= c (4/5) (1/2)2 (1/2)4 |
| P(es war der Würfel) |
= c P(Würfel) P(011011|Würfel) |
= c (1/5) (1/3)2 (2/3)4 |
|
(8) |
Die Summe der beiden
Wahrscheinlichkeiten muss 1 sein. Das bestimmt c,
und wir erhalten P(es war die Münze) » 0.7401
und P(es war der Würfel) » 0.2599.
Wir würden also diesmal auf Münze setzen, sollten uns aber
nicht allzu sicher sein: Mit immerhin 26%iger
Wahrscheinlichkeit verlieren wir die Wette!
Wenn n
Würfe gemacht wurden und die relative Häufigkeit der 0er
und 1er
exakt mit der Wahrscheinlichkeitsverteilung der Münze übereinstimmen,
nimmt die Wahrscheinlichkeit, dass es dennoch der Würfel war, mit
zunehmendem n
exponentiell ab, aber mit kleinem Vorfaktor im Exponenten. Selbst bei
n = 60
liegt sie immerhin noch bei 0.7%!
Dabei können
wir eine interessante Beobachtung machen: Je größer n
ist, umso weniger fällt die Apriori-Wahrscheinlichkeit ins Gewicht!
Ändern wir unser Spiel dahingehend ab, dass wir zunächst
keinerlei Anhaltspunkt für Apriori-Wahrscheinlichkeiten
haben. (Münze und Würfel können beispielsweise für
zwei Theorien über einen Naturprozess stehen).
Was bleibt uns also anderes übrig, als jeder der beiden Möglichkeiten
die Apriori-Wahrscheinlichkeit 1/2
zuzuordnen? Andererseits ist das auch nicht sehr befriedigend. Die
Wahrscheinlichkeitsrechnung kann dieses Dilemma nicht lösen,
aber sie schwächt es ab, wenn viele Beobachtungsdaten vorliegen:
Je größer n
ist, umso weniger kommt es auf die willkürlich angenommenen Apriori-Wahrscheinlichkeiten
an. Was dann zählt, sind in erster Linie die Wahrscheinlichkeiten
P(A|Münze)
und P(A|Würfel).
Ist eine von ihnen sehr viel größer als die andere, so
kann auch eine Gewichtung mit Zahlen der Größenordnung
1
daran nichts ändern. Steht A
beispielsweise für eine Folge aus 19 0ern
und 41 1ern,
so ist P(A|Münze) » 8.67 × 10-19
und P(A|Würfel) » 5.19 × 10-17,
also P(A|Würfel) : P(A|Münze) » 60.
Werden Münze und Würfel mit größenordnungsmäßig
ähnlichen Apriori-Wahrscheinlichkeiten gewichtet, so ändert
sich nichts daran, dass der Würfel wesentlich besser abschneidet!
Was allerdings
auch bei großem n
bestehen bleibt, ist die Schwierigkeit, den Grad der Sicherheit, mit
dem man die Ursache der beobachteten Folge nun kennt, genau zu quantifizieren.
Hier haben wir letzlich den Grund dafür, warum der Satz von Bayes
in den Darlegungen der statistischen Standardmethoden eine eher untergeordnete
Rolle spielt, warum der Begriff der Apriori-Wahrscheinlichkeit selten
erwähnt wird, und warum der Grad an Sicherheit nicht als Wahrscheinlichkeit,
sondern in Form anderer Begriffe (wie das Signifikanzniveau) ausgedrückt
wird.
Eine typische Anwendung
des Bayesschen Satzes ergibt sich aus folgender Situation: Ein Symptom
S
kann von zwei bekannten Krankheiten A
und B
hervorgerufen werden (sagen wir, A
sei selten und gefährlich, B
sei häufig und harmlos), aber auch bei gesunden Menschen (C)
auftreten. Wenn das Symptom bei jemandem auftritt, möchte man wissen,
mit welcher Wahrscheinlichkeit er welche Krankheit hat. Epidemiologische
und medizinische Untersuchungen studieren normalerweise nicht direkt
diese Frage, sondern die Häufigkeit von Symptomen bei gegebenen
Krankheiten, beispielsweise
| Kategorie |
Auftreten
von S
mit Wahrscheinlichkeit |
| A |
0.5 |
| B |
0.2 |
| C |
0.1 |
und die Erkrankungswahrscheinlichkeiten,
beispielsweise
| Kategorie |
Erkrankung
erfolgt mit
Wahrscheinlichkeit |
| A |
0.01 |
| B |
0.15 |
woraus wir schließen,
dass mit Wahrscheinlichkeit 0.84
keine der beiden Krankheiten (sondern Kategorie C)
vorliegt. Mit Hilfe dieser Daten können wir die gestellte Frage
beantworten. Die erste Tabelle definiert drei Zufallsprozesse A,
B
und C.
Die zweite legt fest, mit welchen Apriori-Wahrscheinlichkeiten sie auftreten.
Das zugehörige Baumdiagramm sieht so aus:
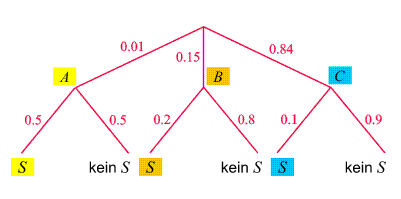
Bei Auftreten des
Symptoms S
sind die Wahrscheinlichkeiten, an A
bzw. B
erkrankt bzw. gesund zu sein, gemäß dem Bayesschen Satz (6)
durch
| P(A|S) = |
0.01 × 0.5
|
» 0.042 |
|
|
0.01 × 0.5 + 0.15 × 0.2 + 0.84 × 0.1
|
|
(9) |
| P(B|S) = |
0.15 × 0.2
|
» 0.252 |
|
|
0.01 × 0.5 + 0.15 × 0.2 + 0.84 × 0.1
|
|
(10) |
| P(C|S) = |
0.84 × 0.1
|
» 0.706 |
|
|
0.01 × 0.5 + 0.15 × 0.2 + 0.84 × 0.1
|
|
(11) |
gegeben. Unser
Patient braucht sich also keine übermäßigen Sorgen zu
machen (obwohl eine Abklärung sinnvoll ist, denn von 1000
Patienten, bei denen das Symptom auftritt, werden ungefähr 40
tatsächlich an A
erkrankt sein).
Situationen
wie die vorliegende werden oft auch anhand von Mengendiagrammen wie
diesem
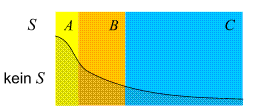
visualisiert.
Aus ihm gehen die Kombinationsmöglichkeiten (A,
B
oder C,
jeweils mit oder ohne S)
hervor. Bedingte Wahrscheinlichkeiten können hier als Flächeninhalte
interpretiert werden, und der Satz von Bayes ist dann eine Aussage
über Beziehungen zwischen diesen Flächeninhalten.
|





