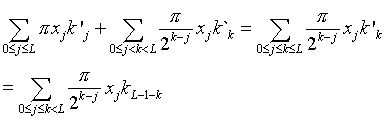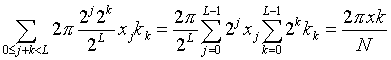Finden der Periode einer Funktion
Peter Klimek, WS 2003/4
Wir nennen |xi> ein qubit, welches in der Standarbasis {|0>, |1>} gegeben sei, der zugehörige Zustandsraum ist der 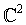 . Einen String von L qubits nennen wir ein Register. In ihm ist die Information in binärer Form enthalten:
. Einen String von L qubits nennen wir ein Register. In ihm ist die Information in binärer Form enthalten:
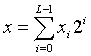 In der Dirac Notation lässt sich ein Register als Tensorprodukt schreiben:
In der Dirac Notation lässt sich ein Register als Tensorprodukt schreiben:
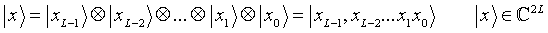 Unsere Problemstellung ist das Finden der Periode einer Funktion
Unsere Problemstellung ist das Finden der Periode einer Funktion 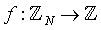 , wobei
, wobei 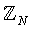 eine Gruppe von Integers modulo N bezeichnet. Weiters nehme f innerhalb einer Periode einen Funktionswert nicht zweimal an.
eine Gruppe von Integers modulo N bezeichnet. Weiters nehme f innerhalb einer Periode einen Funktionswert nicht zweimal an.
Wir benötigen zwei L qubit Register:
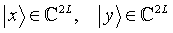 Der Input im |x> Register ist der Superpostionszustand:
Der Input im |x> Register ist der Superpostionszustand:
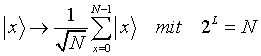 Die Werte im |y> Register seien |yi>=0 für alle i.
Die Werte im |y> Register seien |yi>=0 für alle i.
Die Vorgangsweise lässt sich als Schaltbild verdeutlichen:
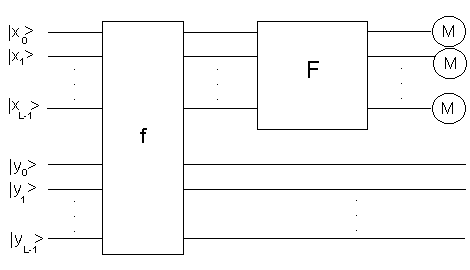 Wir beginnen indem wir das ganze System, beschrieben durch
Wir beginnen indem wir das ganze System, beschrieben durch 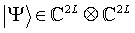 , in folgenden Superpositionszustand der beiden Register bringen:
, in folgenden Superpositionszustand der beiden Register bringen:
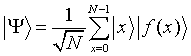 Um daraus die Information über die Periode zu destillieren, führen wir eine Fouriertransformation im |x> Register durch:
Um daraus die Information über die Periode zu destillieren, führen wir eine Fouriertransformation im |x> Register durch:
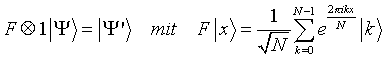 und erhalten den Zustand
und erhalten den Zustand
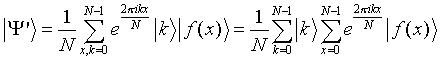 Zur Auswertung führen wir eine Messung in der Standardbasis {|0>, |1>} im |x> Register durch und erhalten den Wert k. N ist die Anzahl der digitalen Zustände unseres Inputs in |x>, T die Periode und N durch T teilbar. Unsere möglichen Messwerte sind dann:
Zur Auswertung führen wir eine Messung in der Standardbasis {|0>, |1>} im |x> Register durch und erhalten den Wert k. N ist die Anzahl der digitalen Zustände unseres Inputs in |x>, T die Periode und N durch T teilbar. Unsere möglichen Messwerte sind dann:
 die wir alle mit der gleichen Wahrscheinlichkeit erhalten können, weil alle Amplituden von F|x> gleich sind.
Um dies näher zu illustrieren, betrachten wir ein Beispiel mit L=1. Die möglichen Perioden sind dann T=1,2. Für T=1 ist die Funktion konstant: f(0)=f(1). Für T=2 gilt f(0)=1+f(1) mod(2). Die Fragestellung ähnelt also der des Deutsch-Algorithmus. Wir gehen w.o. beschrieben vor:
die wir alle mit der gleichen Wahrscheinlichkeit erhalten können, weil alle Amplituden von F|x> gleich sind.
Um dies näher zu illustrieren, betrachten wir ein Beispiel mit L=1. Die möglichen Perioden sind dann T=1,2. Für T=1 ist die Funktion konstant: f(0)=f(1). Für T=2 gilt f(0)=1+f(1) mod(2). Die Fragestellung ähnelt also der des Deutsch-Algorithmus. Wir gehen w.o. beschrieben vor:
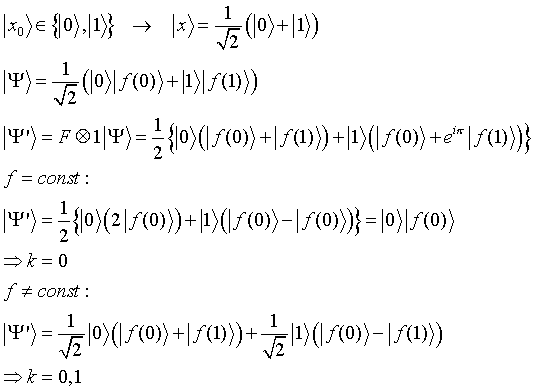 Im ersten Fall erhalten wir ein eindeutiges Ergebnis. Unter Verwendung der Periodizität der Funktion heben sich die komplexen Phasen für einen Zustand auf, im zweiten Fall erhalte ich zwei Zustände mit der gleichen Wahrscheinlichkeit, die möglichen Resultate sind k=0,1.
Im ersten Fall erhalten wir ein eindeutiges Ergebnis. Unter Verwendung der Periodizität der Funktion heben sich die komplexen Phasen für einen Zustand auf, im zweiten Fall erhalte ich zwei Zustände mit der gleichen Wahrscheinlichkeit, die möglichen Resultate sind k=0,1.
Die Funktionsweise lässt sich so zusammenfassen: Im ursprünglichen Zustand des Systems waren die Amplituden periodisch mit T und besaßen eine zufällige Phase x: f(x)=f(x+T). Durch die Fourier-Transformation verschwindet diese Phase und die Periodizität wird umgekehrt zu N/T. Daher sind die möglichen Messwerte k Vielfache dieses Ausdrucks.
Betrachten wir ein anderes Beispiel: sei T=8, L=7, d.h. N=128. Die Messung liefert dann 8 mögliche Werte: k=0, 16, 32, 48,... 112. Wir bilden nun N/k und kürzen so weit wie möglich:
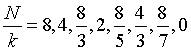 Wenn wir einen Wert erhalten, bei dem m und T keinen gemeinsamen Teiler außer 1 haben, können wir die Periode ablesen. Hier beträgt diese Wahrscheinlichkeit 1/2.
Allgemein finden wir die Periode dadurch, dass wir N/k auf den kleinsten möglichen Nenner kürzen. Wenn das zufällig gewählte m keinen gemeinsamen Teiler mit T außer 1 hat, können wir die Periode direkt ablesen. Wie groß ist nun die Wahrscheinlichkeit, dass wir so einen Treffer erzielen? Dem Primzahlentheorem zufolge (siehe Jozsa, Ekert, Rev. Mod. Phys. 68, (1996), Appendix A) geht die Anzahl der Primzahlen kleiner als T für große T wie T/logT. D.h. Die Wahrscheinlichkeit, ein solches m zu finden, beträgt 1/logT. Wenn wir also O(1/logN) Aufrufe machen, können wir T mit einer Wahrscheinlichkeit bestimmen, die so nahe bei 1 ist, wie wir wünschen.
Wenn wir einen Wert erhalten, bei dem m und T keinen gemeinsamen Teiler außer 1 haben, können wir die Periode ablesen. Hier beträgt diese Wahrscheinlichkeit 1/2.
Allgemein finden wir die Periode dadurch, dass wir N/k auf den kleinsten möglichen Nenner kürzen. Wenn das zufällig gewählte m keinen gemeinsamen Teiler mit T außer 1 hat, können wir die Periode direkt ablesen. Wie groß ist nun die Wahrscheinlichkeit, dass wir so einen Treffer erzielen? Dem Primzahlentheorem zufolge (siehe Jozsa, Ekert, Rev. Mod. Phys. 68, (1996), Appendix A) geht die Anzahl der Primzahlen kleiner als T für große T wie T/logT. D.h. Die Wahrscheinlichkeit, ein solches m zu finden, beträgt 1/logT. Wenn wir also O(1/logN) Aufrufe machen, können wir T mit einer Wahrscheinlichkeit bestimmen, die so nahe bei 1 ist, wie wir wünschen.
Diskrete Fouriertransformation
Wir wollen nun diskutieren, wie man eine diskrete Fouriertransformation mittels zwei unitärer Operatoren durchführen kann.
Dazu führen wir den one-qubit-Operator Aj ein, der auf das j. qubit wirkt. Er ist gegeben durch
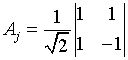 In dieser Darstellung sind die Zeilen und Spalten mit den Zuständen |0> und |1> indiziert, d.h. die erste Zeile bzw. Spalte wirkt auf |0>.
Wir führen auch noch einen two-qubit-Operator Bj,k ein. Er wirkt auf das j. und k. qubit, wobei die Zeilen und Spalten mit |00>, |01>, |10> und |11> indiziert sind.
In dieser Darstellung sind die Zeilen und Spalten mit den Zuständen |0> und |1> indiziert, d.h. die erste Zeile bzw. Spalte wirkt auf |0>.
Wir führen auch noch einen two-qubit-Operator Bj,k ein. Er wirkt auf das j. und k. qubit, wobei die Zeilen und Spalten mit |00>, |01>, |10> und |11> indiziert sind.
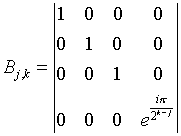 Er liefert nur dann einen Beitrag, wenn beide qubits gleich |1> sind.
Um eine diskrete Fouriertransformation durchzuführen, muss man diese Operatoren in folgender Reihenfolge anwenden:
Er liefert nur dann einen Beitrag, wenn beide qubits gleich |1> sind.
Um eine diskrete Fouriertransformation durchzuführen, muss man diese Operatoren in folgender Reihenfolge anwenden:
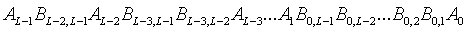 Anschließend muss man noch die Reihenfolge der qubits umkehren (bit-reversal), d.h. man liest die Ergebnisse in umgekehrter Reihenfolge ab.
Anschließend muss man noch die Reihenfolge der qubits umkehren (bit-reversal), d.h. man liest die Ergebnisse in umgekehrter Reihenfolge ab.
Das zugehörige Schaltbild lässt sich folgenderweise rekursiv darstellen:
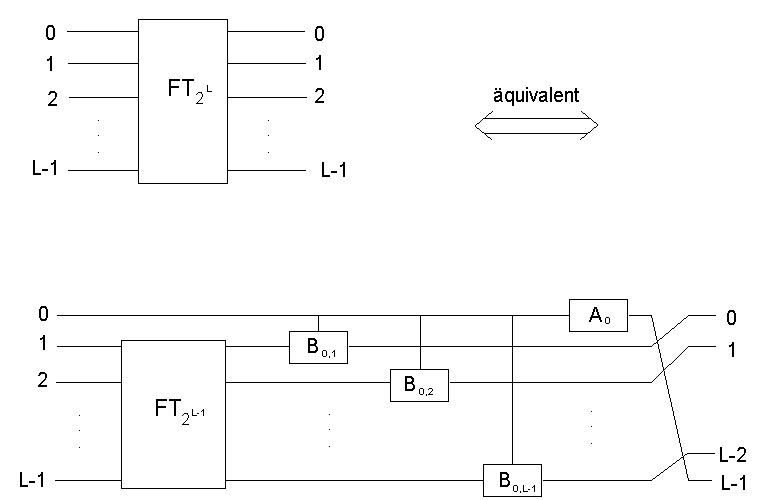 Wir wollen nun zeigen, dass diese Operatoren das gewünschte leisten. Aj wird L mal ausgeführt und produziert den overall Faktor N-1/2. Es bleibt noch zu klären, wie der Phasenfaktor zu Stande kommt. Aj liefert
Wir wollen nun zeigen, dass diese Operatoren das gewünschte leisten. Aj wird L mal ausgeführt und produziert den overall Faktor N-1/2. Es bleibt noch zu klären, wie der Phasenfaktor zu Stande kommt. Aj liefert 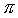 , wenn xj=k'j=1. Bj,k produziert den Phasenfaktor
, wenn xj=k'j=1. Bj,k produziert den Phasenfaktor 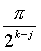 wenn xj=k'k=1.
Mit k ist das bit-reversal von k' gemeint. Für die Phase ergibt sich dann folgendes:
wenn xj=k'k=1.
Mit k ist das bit-reversal von k' gemeint. Für die Phase ergibt sich dann folgendes:
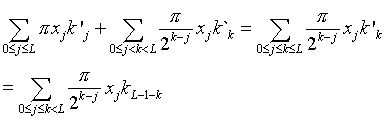 Wir substituieren nun die Indizes: L-1-k=k
Wir substituieren nun die Indizes: L-1-k=k
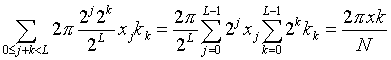 Die eingeführten Operatoren realisieren also tatsächlich eine diskrete Fouriertransformation.
Die eingeführten Operatoren realisieren also tatsächlich eine diskrete Fouriertransformation.
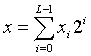
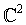 . Einen String von L qubits nennen wir ein Register. In ihm ist die Information in binärer Form enthalten:
. Einen String von L qubits nennen wir ein Register. In ihm ist die Information in binärer Form enthalten: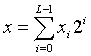
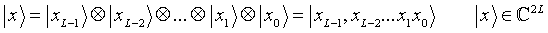
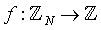 , wobei
, wobei 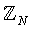 eine Gruppe von Integers modulo N bezeichnet. Weiters nehme f innerhalb einer Periode einen Funktionswert nicht zweimal an.
eine Gruppe von Integers modulo N bezeichnet. Weiters nehme f innerhalb einer Periode einen Funktionswert nicht zweimal an.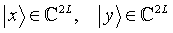
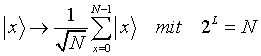

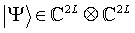 , in folgenden Superpositionszustand der beiden Register bringen:
, in folgenden Superpositionszustand der beiden Register bringen: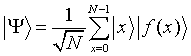
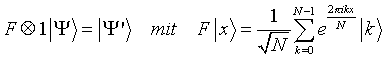
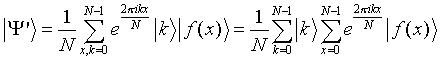

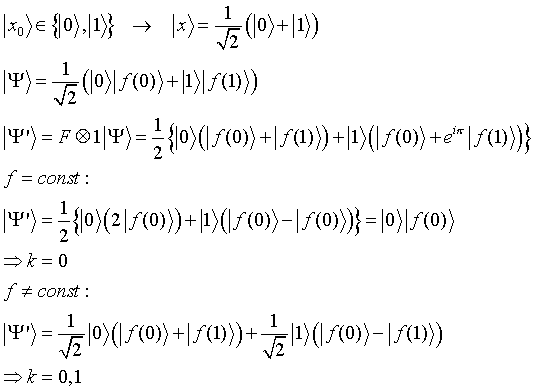
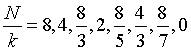
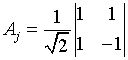
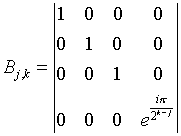
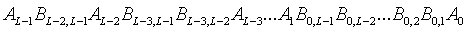

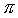 , wenn xj=k'j=1. Bj,k produziert den Phasenfaktor
, wenn xj=k'j=1. Bj,k produziert den Phasenfaktor 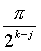 wenn xj=k'k=1.
Mit k ist das bit-reversal von k' gemeint. Für die Phase ergibt sich dann folgendes:
wenn xj=k'k=1.
Mit k ist das bit-reversal von k' gemeint. Für die Phase ergibt sich dann folgendes: